《2025年5年中考3年模拟九年级数学下册沪科版》

14.(2022安徽中考,7,★★☆)已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB =6,则OP= （ ）
A.$\sqrt{14}$
B.4
C.$\sqrt{23}$
D.5

答案：
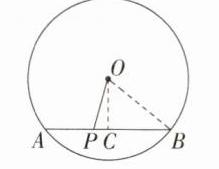
D：如图，过点O作OC⊥AB于点C，连接OB，则OB = 7；因为PA = 4，PB = 6，所以AB = PA + PB = 10；因为OC⊥AB，所以AC = BC = 5，所以PC = PB - BC = 1；在Rt△OBC中，根据勾股定理，得$OC^{2}=OB^{2}-BC^{2}=7^{2}-5^{2}=24$；在Rt△OPC中，根据勾股定理，得$OP=\sqrt{OC^{2}+PC^{2}}=\sqrt{24 + 1}=5$，故选D。

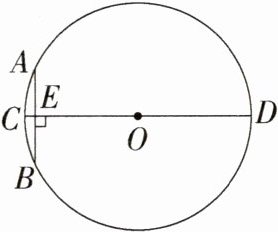
15.情境题·数学文化 (2023山东东营中考,16,★★☆)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”转化为现在的数学语言表达就是:如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 10寸,则直径CD的长度为________寸.(M9224006)

答案：
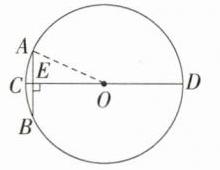
答案：26 解析：如图，连接OA，设⊙O的半径是r寸，因为直径CD⊥AB，所以$AE=\frac{1}{2}AB=\frac{1}{2}\times10 = 5$寸；因为CE = 1寸，所以OE = (r - 1)寸；因为$OA^{2}=OE^{2}+AE^{2}$，所以$r^{2}=(r - 1)^{2}+5^{2}$，所以r = 13，所以直径CD的长度为26寸。

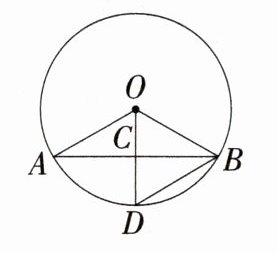
16.(2024安徽界首五中一模,21,★★☆)一条水管内有少量水,截面如图所示,水面AB垂直平分半径OD,交OD于点C,连接OA,OB,BD.
(1)求∠ODB的度数.
(2)若⊙O的半径为6,求弦AB的长.
(3)连接AD，请判断四边形AOBD的形状，并给出证明

答案：
解析\n
(1)因为AB垂直平分OD，所以OB = DB；因为OB = OD，所以OB = OD = DB，所以△OBD为等边三角形，所以∠ODB = 60°。\n
(2)因为⊙O的半径为6，所以OB = OD = 6；又因为AB垂直平分OD，所以OD⊥AB，且$OC=\frac{1}{2}OD=\frac{1}{2}\times6 = 3$，所以$BC=\sqrt{OB^{2}-OC^{2}}=\sqrt{6^{2}-3^{2}}=3\sqrt{3}$；因为OD⊥AB，OD为⊙O的半径，所以AC = BC，所以AB = 2BC = $6\sqrt{3}$。\n
(3)四边形AOBD为菱形。 证明：如图。因为AB垂直平分OD，所以OA = DA，OB = DB；又因为OA = OB，所以OA = DA = DB = OB，所以四边形AOBD为菱形。

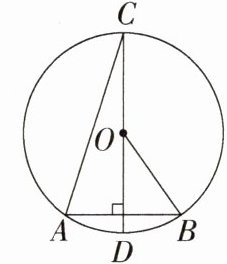
例 如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=10,AB=12,则AC的长为________.

答案： 答案：$6\sqrt{10}$ 解析：设AB和CD交于E（图略），因为CD⊥AB，CD是直径，AB = 12，所以AE = BE = 6，∠OEB = ∠CEA = 90°；在Rt△OEB中，由勾股定理，得$OE=\sqrt{OB^{2}-BE^{2}}=\sqrt{10^{2}-6^{2}} = 8$，所以CE = OC + OE = 10 + 8 = 18；在Rt△ACE中，由勾股定理，得$AC=\sqrt{CE^{2}+AE^{2}}=\sqrt{18^{2}+6^{2}}=6\sqrt{10}$。

变式
1.(2024甘肃武威期末)如图,⊙O的弦AB⊥OC,垂足为D,且OD=2DC,AB=2$\sqrt{5}$,则⊙O的半径是________.

答案： 答案：3 解析：因为⊙O的弦AB⊥OC，$AB = 2\sqrt{5}$，所以$AD = BD=\frac{1}{2}AB=\sqrt{5}$，∠ADO = 90°；设⊙O的半径是r，则OA = OC = r；因为OD = 2DC，所以$OD=\frac{2}{3}OC=\frac{2}{3}r$；在Rt△ADO中，$OA^{2}=OD^{2}+AD^{2}$，所以$r^{2}=(\frac{2}{3}r)^{2}+(\sqrt{5})^{2}$，解得r = 3或r = - 3（不合题意，舍去），即⊙O的半径是3。

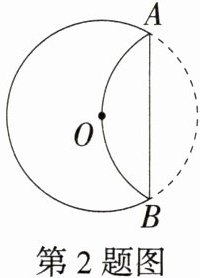
2.如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O.如果弦AB=4$\sqrt{3}$,那么⊙O的半径长为________.

答案：
答案：4 解析：如图，作OD⊥AB于D，连接OA。因为OD⊥AB，$AB = 4\sqrt{3}$，所以$AD=\frac{1}{2}AB = 2\sqrt{3}$；由折叠得$OD=\frac{1}{2}AO$，设OD = x，则AO = 2x；在Rt△OAD中，$AD^{2}+OD^{2}=OA^{2}$，即$(2\sqrt{3})^{2}+x^{2}=(2x)^{2}$，解得x = 2或x = - 2（不合题意，舍去），所以OA = 2x = 4，即⊙O的半径长为4。