第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
22. [答案含评分细则](8分)
(1)如图1,在△ABC中,∠ABC = 130°,将△ABC绕点C逆时针旋转50°,得到△A'B'C,连接BB',求∠A'B'B的大小.
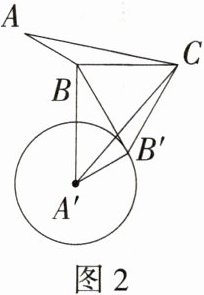
(2)如图2,在△ABC中,∠ABC = 150°,AB = 3,BC = 5,将△ABC绕点C逆时针旋转60°得到△A'B'C,连接BB',以A'为圆心,A'B'的长为半径作圆.
①猜想:直线BB'与⊙A'的位置关系,并证明你的结论;
②连接A'B,求线段A'B的长度.
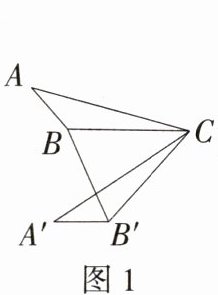
(1)如图1,在△ABC中,∠ABC = 130°,将△ABC绕点C逆时针旋转50°,得到△A'B'C,连接BB',求∠A'B'B的大小.
(2)如图2,在△ABC中,∠ABC = 150°,AB = 3,BC = 5,将△ABC绕点C逆时针旋转60°得到△A'B'C,连接BB',以A'为圆心,A'B'的长为半径作圆.
①猜想:直线BB'与⊙A'的位置关系,并证明你的结论;
②连接A'B,求线段A'B的长度.


答案:
解析:(1)由旋转变换的性质可知,∠A′B′C = ∠ABC = 130°,∠BCB′ = 50°,CB = CB′,
∴ ∠CB′B = 65°,
∴ ∠A′B′B = ∠A′B′C - ∠CB′B = 65°. …… 3 分 (2)①直线 BB′与⊙A′相切. 证明:由旋转可知,∠A′B′C = ∠ABC = 150°,∠BCB′ = 60°,CB = CB′,
∴ △CBB′是等边三角形,
∴ ∠CB′B = 60°,
∴ ∠A′B′B = ∠A′B′C - ∠CB′B = 90°,
∵ A′B′为半径,
∴ 直线 BB′与⊙A′相切. …… 6 分 ②在 Rt△A′B′B 中,∠A′B′B = 90°,BB′ = BC = 5,A′B′ = AB = 3,
∴ $A′B=\sqrt{A′B′^{2}+B′B^{2}}=\sqrt{34}$. …… 8 分
∴ ∠CB′B = 65°,
∴ ∠A′B′B = ∠A′B′C - ∠CB′B = 65°. …… 3 分 (2)①直线 BB′与⊙A′相切. 证明:由旋转可知,∠A′B′C = ∠ABC = 150°,∠BCB′ = 60°,CB = CB′,
∴ △CBB′是等边三角形,
∴ ∠CB′B = 60°,
∴ ∠A′B′B = ∠A′B′C - ∠CB′B = 90°,
∵ A′B′为半径,
∴ 直线 BB′与⊙A′相切. …… 6 分 ②在 Rt△A′B′B 中,∠A′B′B = 90°,BB′ = BC = 5,A′B′ = AB = 3,
∴ $A′B=\sqrt{A′B′^{2}+B′B^{2}}=\sqrt{34}$. …… 8 分
23. [答案含评分细则](10分)小明学习了垂径定理后,做了下面的探究,请根据题目要求帮小明完成探究.
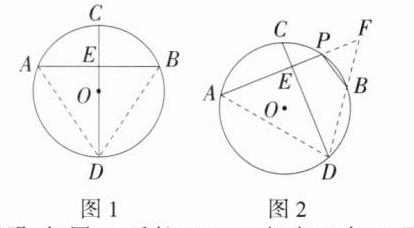
(1)如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE = BE. 请证明此结论.
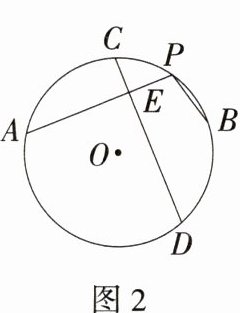
(2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦. 如图2,PA,PB组成⊙O的一条折弦. C是劣弧AB的中点,直线CD⊥PA于点E,则AE = PE + PB. 请写出证明过程.(提示:通过延长DB、AP相交于点F,再连接AD证明结论成立)
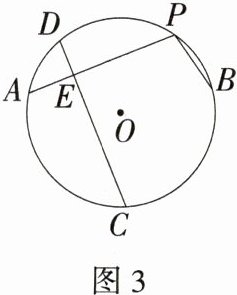
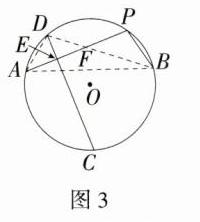
(3)如图3,PA,PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.
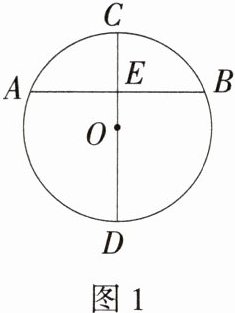
(1)如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE = BE. 请证明此结论.
(2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦. 如图2,PA,PB组成⊙O的一条折弦. C是劣弧AB的中点,直线CD⊥PA于点E,则AE = PE + PB. 请写出证明过程.(提示:通过延长DB、AP相交于点F,再连接AD证明结论成立)
(3)如图3,PA,PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.



答案:
解析:(1)证明:如图 1,连接 AD,BD,
∵ C 是劣弧 AB 的中点,
∴ ∠CDA = ∠CDB, …… 1 分
∵ DE⊥AB,
∴ ∠AED = ∠DEB = 90°,
∴ ∠A + ∠ADE = 90°,∠B + ∠CDB = 90°,
∴ ∠A = ∠B, …… 2 分
∴ △ADB 为等腰三角形,
∵ CD⊥AB,
∴ AE = BE. …… 3 分 (2)证明:如图 2,延长 DB、AP 相交于点 F,再连接 AD,
∵ 四边形 ADBP 是圆内接四边形,
∴ ∠PBF = ∠A, …… 4 分
∵ C 是劣弧 AB 的中点,
∴ ∠CDA = ∠CDF,
∵ CD⊥PA,
∴ △AFD 为等腰三角形, …… 5 分
∴ ∠F = ∠A,AE = EF,
∴ ∠PBF = ∠F,
∴ PB = PF,
∴ AE = PE + PB. …… 6 分 (3)AE = PE - PB. …… 10 分 **详解**:如图 3,连接 AD,BD,AB,DB、AP 相交于点 F,
∵ C 是优弧 AB 的中点,
∴ $\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴ ∠ADC = ∠BDC,
∵ CD⊥AP,
∴ ∠DEA = ∠DEF, 又
∵ DE = DE,
∴ △DAE≌△DFE,
∴ AE = EF,∠DAF = ∠DFA,
∵ ∠DFA = ∠PFB,∠PBD = ∠DAP,
∴ ∠PFB = ∠PBF,
∴ PF = PB,
∴ AE = PE - PB.
解析:(1)证明:如图 1,连接 AD,BD,
∵ C 是劣弧 AB 的中点,
∴ ∠CDA = ∠CDB, …… 1 分
∵ DE⊥AB,
∴ ∠AED = ∠DEB = 90°,
∴ ∠A + ∠ADE = 90°,∠B + ∠CDB = 90°,
∴ ∠A = ∠B, …… 2 分
∴ △ADB 为等腰三角形,
∵ CD⊥AB,
∴ AE = BE. …… 3 分 (2)证明:如图 2,延长 DB、AP 相交于点 F,再连接 AD,
∵ 四边形 ADBP 是圆内接四边形,
∴ ∠PBF = ∠A, …… 4 分
∵ C 是劣弧 AB 的中点,
∴ ∠CDA = ∠CDF,
∵ CD⊥PA,
∴ △AFD 为等腰三角形, …… 5 分
∴ ∠F = ∠A,AE = EF,
∴ ∠PBF = ∠F,
∴ PB = PF,
∴ AE = PE + PB. …… 6 分 (3)AE = PE - PB. …… 10 分 **详解**:如图 3,连接 AD,BD,AB,DB、AP 相交于点 F,
∵ C 是优弧 AB 的中点,
∴ $\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴ ∠ADC = ∠BDC,
∵ CD⊥AP,
∴ ∠DEA = ∠DEF, 又
∵ DE = DE,
∴ △DAE≌△DFE,
∴ AE = EF,∠DAF = ∠DFA,
∵ ∠DFA = ∠PFB,∠PBD = ∠DAP,
∴ ∠PFB = ∠PBF,
∴ PF = PB,
∴ AE = PE - PB.


查看更多完整答案,请扫码查看


