第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
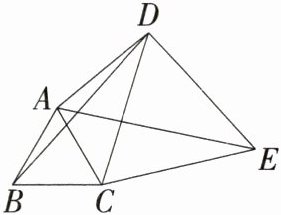
1.(2024广西西大附中月考)如图,在四边形$ABCD$中,$AC$,$BD$是对角线,$\triangle ABC$是等边三角形.线段$CD$绕点$C$顺时针旋转$60^{\circ}$得到线段$CE$,连接$AE$,$DE$.(M9224001)
(1)求证:$\triangle BCD\cong\triangle ACE$.
(2)若$\angle ADC = 30^{\circ}$,$AD = 6$,$BD = 10$,求$DE$的长.
(1)求证:$\triangle BCD\cong\triangle ACE$.
(2)若$\angle ADC = 30^{\circ}$,$AD = 6$,$BD = 10$,求$DE$的长.

答案:
1. **解析**\n(1)**证明**:由旋转可知$\angle DCE = 60^{\circ}$,$CD = CE$。因为$\triangle ABC$是等边三角形,所以$\angle ACB = 60^{\circ}$,$AC = BC$。所以$\angle ACB=\angle DCE = 60^{\circ}$,则$\angle ACB+\angle ACD=\angle DCE+\angle ACD$,即$\angle BCD=\angle ACE$。
在$\triangle BCD$和$\triangle ACE$中,$\begin{cases}BC = AC\\\angle BCD=\angle ACE\\CD = CE\end{cases}$,所以$\triangle BCD\cong\triangle ACE(SAS)$。\n(2)由(1)知$\triangle BCD\cong\triangle ACE$,所以$AE = BD = 10$。因为$\angle DCE = 60^{\circ}$,$CD = CE$,所以$\triangle CDE$是等边三角形,所以$\angle CDE = 60^{\circ}$。又因为$\angle ADC = 30^{\circ}$,所以$\angle ADE=\angle ADC+\angle CDE = 90^{\circ}$。在$Rt\triangle ADE$中,$DE=\sqrt{AE^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}} = 8$。
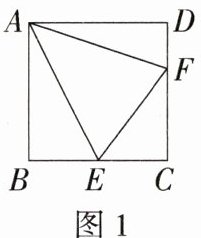
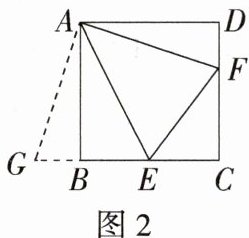
2.(2024浙江绍兴期中)如图1,四边形$ABCD$是正方形,$E$,$F$分别在边$BC$和$CD$上,且$\angle EAF = 45^{\circ}$,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图2,小明为了探究线段$EF$,$BE$,$DF$之间的关系,将$\triangle ADF$绕点$A$顺时针旋转了$90^{\circ}$.
(1)请直接写出线段$EF$,$BE$,$DF$之间的数量关系.
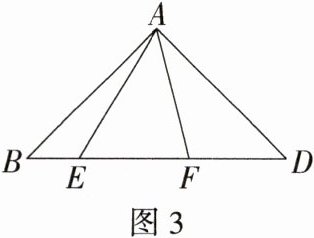
(2)如图3,在等腰直角三角形$ABD$中,$\angle BAD = 90^{\circ}$,$AB = AD$,点$E$,$F$在边$BD$上,且$\angle EAF = 45^{\circ}$,请写出$EF$,$BE$,$DF$之间的关系,并说明理由.
(1)请直接写出线段$EF$,$BE$,$DF$之间的数量关系.
(2)如图3,在等腰直角三角形$ABD$中,$\angle BAD = 90^{\circ}$,$AB = AD$,点$E$,$F$在边$BD$上,且$\angle EAF = 45^{\circ}$,请写出$EF$,$BE$,$DF$之间的关系,并说明理由.



答案:
2. **解析**\n(1)$EF = BE + DF$。**详解**:由旋转可得$GB = DF$,$AG = AF$,$\angle BAG=\angle DAF$,易知$G$,$B$,$E$三点在同一直线上。因为四边形$ABCD$为正方形,所以$\angle BAD = 90^{\circ}$。因为$\angle EAF = 45^{\circ}$,所以$\angle BAE+\angle DAF = 45^{\circ}$,所以$\angle BAG+\angle BAE = 45^{\circ}$,即$\angle GAE=\angle EAF$。在$\triangle AGE$和$\triangle AFE$中,$\begin{cases}AG = AF\\\angle GAE=\angle FAE\\AE = AE\end{cases}$,所以$\triangle AGE\cong\triangle AFE(SAS)$,所以$GE = EF$。因为$GE = GB + BE = BE + DF$,所以$EF = BE + DF$。\n(2)$EF^{2}=BE^{2}+DF^{2}$。**理由**:把$\triangle AFD$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle AE'B$,连接$EE'$,如图。 所以$BE' = FD$,$AE' = AF$,$\angle D=\angle ABE'$,$\angle FAD=\angle E'AB$。因为$AB = AD$,所以$\angle ABD=\angle ADB = 45^{\circ}$,所以$\angle ABD+\angle ABE' = 90^{\circ}$,即$\angle E'BD = 90^{\circ}$,所以$E'B^{2}+BE^{2}=E'E^{2}$。又因为$\angle FAE = 45^{\circ}$,所以$\angle BAE+\angle FAD = 45^{\circ}$,所以$\angle E'AB+\angle BAE = 45^{\circ}$,即$\angle E'AE = 45^{\circ}$。在$\triangle AEE'$和$\triangle AEF$中,$\begin{cases}AE = AE\\\angle E'AE=\angle FAE\\AE' = AF\end{cases}$,所以$\triangle AEE'\cong\triangle AEF(SAS)$,所以$EE' = FE$,所以$EF^{2}=BE^{2}+DF^{2}$。
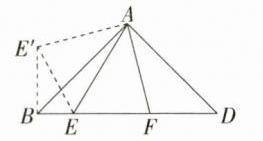
2. **解析**\n(1)$EF = BE + DF$。**详解**:由旋转可得$GB = DF$,$AG = AF$,$\angle BAG=\angle DAF$,易知$G$,$B$,$E$三点在同一直线上。因为四边形$ABCD$为正方形,所以$\angle BAD = 90^{\circ}$。因为$\angle EAF = 45^{\circ}$,所以$\angle BAE+\angle DAF = 45^{\circ}$,所以$\angle BAG+\angle BAE = 45^{\circ}$,即$\angle GAE=\angle EAF$。在$\triangle AGE$和$\triangle AFE$中,$\begin{cases}AG = AF\\\angle GAE=\angle FAE\\AE = AE\end{cases}$,所以$\triangle AGE\cong\triangle AFE(SAS)$,所以$GE = EF$。因为$GE = GB + BE = BE + DF$,所以$EF = BE + DF$。\n(2)$EF^{2}=BE^{2}+DF^{2}$。**理由**:把$\triangle AFD$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle AE'B$,连接$EE'$,如图。 所以$BE' = FD$,$AE' = AF$,$\angle D=\angle ABE'$,$\angle FAD=\angle E'AB$。因为$AB = AD$,所以$\angle ABD=\angle ADB = 45^{\circ}$,所以$\angle ABD+\angle ABE' = 90^{\circ}$,即$\angle E'BD = 90^{\circ}$,所以$E'B^{2}+BE^{2}=E'E^{2}$。又因为$\angle FAE = 45^{\circ}$,所以$\angle BAE+\angle FAD = 45^{\circ}$,所以$\angle E'AB+\angle BAE = 45^{\circ}$,即$\angle E'AE = 45^{\circ}$。在$\triangle AEE'$和$\triangle AEF$中,$\begin{cases}AE = AE\\\angle E'AE=\angle FAE\\AE' = AF\end{cases}$,所以$\triangle AEE'\cong\triangle AEF(SAS)$,所以$EE' = FE$,所以$EF^{2}=BE^{2}+DF^{2}$。

查看更多完整答案,请扫码查看


