《2025年5年中考3年模拟九年级数学下册沪科版》

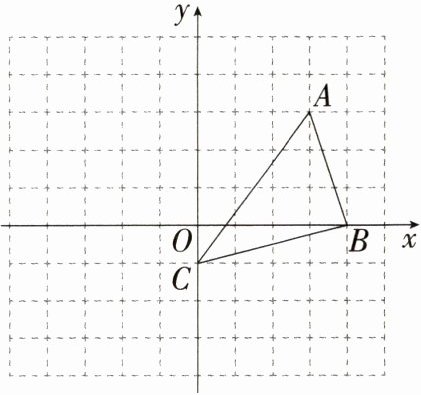
16. [答案含评分细则](2024广西贵港港南期末)(6分)如图，在平面直角坐标系中，△ABC的顶点为A(3,3)，B(4,0)，C(0,-1).
(1)作出△ABC关于原点对称的△A₁B₁C₁.
(2)作出△ABC绕点C逆时针旋转90°后得到的△A₂B₂C.
(3)点B的对应点B₂的坐标为_______.

答案：
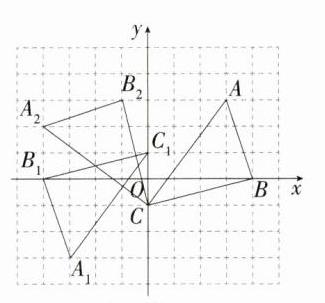
解析：（1）如图，△A₁B₁C₁ 即为所求. …… 2 分 （2）如图，△A₂B₂C 即为所求. …… 4 分 （3）(-1,3). …… 6 分

17. [答案含评分细则](2024安徽怀远模拟)(6分)情暖金秋，爱在重阳. 为弘扬中华优秀传统文化，营造尊老、爱老、助老氛围，重阳节上午，某医院医护人员将前往幸福社区开展重阳节关爱老年人健康义诊活动，为配合义诊活动，该社区居委会计划从A小区的甲、乙与B小区的丙、丁中招募两名志愿者.
(1)甲成为志愿者是__________(填“必然事件”或“随机事件”).
(2)用列表法或画树状图法，求所招募的两名志愿者恰好来自同一小区的概率.

答案： 解析：（1）随机事件. …… 2 分 （2）根据题意，用列表法表示所有可能出现的结果如下： | |甲|乙|丙|丁| | ---- | ---- | ---- | ---- | ---- | |甲|—|乙甲|丙甲|丁甲| |乙|甲乙|—|丙乙|丁乙| |丙|甲丙|乙丙|—|丁丙| |丁|甲丁|乙丁|丙丁|—| …… 4 分 共有 12 种等可能出现的结果，其中所招募的两名志愿者恰好来自同一小区的结果有 4 种，
∴ 所招募的两名志愿者恰好来自同一小区的概率为$\frac{4}{12}=\frac{1}{3}$. …… 6 分

18. [答案含评分细则](2023重庆八中期中)(6分)一水壶可近似地看成由两个圆柱叠成的几何体. 主视图和俯视图如图所示. 请根据图中数据求底部圆柱的侧面积以及该几何体的体积.(结果均保留π)

答案： 解析：$\pi\times16\times16 = 256\pi$. 故底部圆柱的侧面积为 256π. …… 3 分 $\pi\times(\frac{16}{2})^{2}\times16+\pi\times(\frac{8}{2})^{2}\times4 = 1024\pi+64\pi = 1088\pi$. 故该几何体的体积为 1088π. …… 6 分

19. [答案含评分细则](6分)如图，Rt△ABC中，∠C = 90°，在BC上取一点D使AD = BD，作△ACD的外接圆⊙O，交AB于点E.
(1)求证：AE = BE.
(2)若CD = 3，AB = 4√5，求AC的长.

答案：
解析：（1）证明：如图，连接 DE，
∵ ∠C = 90°，
∴ AD 为⊙O 的直径，
∴ DE⊥AB， …… 2 分 又
∵ AD = BD，
∴ AE = BE. …… 3 分 （2）设 BD = x，由（1）可知∠DEB = 90°，$BE=\frac{1}{2}AB$.
∵ ∠B = ∠B，∠C = ∠DEB = 90°，
∴ △ABC∽△DBE， …… 4 分
∴ $\frac{DB}{AB}=\frac{BE}{BC}$，
∴ $\frac{x}{4\sqrt{5}}=\frac{2\sqrt{5}}{x + 3}$，
∴ $x_{1}=-8$（舍去），$x_{2}=5$，
∴ AD = BD = 5，
∴ $AC=\sqrt{5^{2}-3^{2}} = 4$. …… 6 分