第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024安徽中考)若扇形AOB的半径为6,∠AOB = 120°,则$\overset{\frown}{AB}$的长为(M9224013) ( )
A.2π
B.3π
C.4π
D.6π
A.2π
B.3π
C.4π
D.6π
答案:
C:$\overset{\frown}{AB}$的长$=\frac{n\pi r}{180}=\frac{120\times\pi\times6}{180}=4\pi$,故选C。
2.情境题·劳动生产(2024广东广州南沙一模)一个滑轮起重装置如图所示,滑轮的直径是8 cm,当重物上升2π cm时,滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为(M9224013) ( )
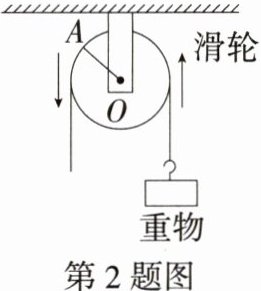
A.60°
B.90°
C.120°
D.180°

A.60°
B.90°
C.120°
D.180°
答案:
B:设旋转的角度是$n$度,根据题意得$\frac{4n\pi}{180}=2\pi$,解得$n = 90$。故选B。
3.新独家原创 如图,△ABC中,∠A = 60°,AB = 2,以点A为圆心,AC长为半径的弧交斜边AB于点D,$\overset{\frown}{CD}$的长为$\frac{\pi}{3}$,则△ABC是 ( )
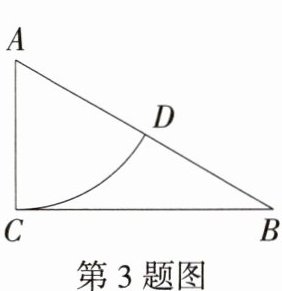
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断

A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断
答案:
B:连接$CD$(图略)。由弧长公式得$\frac{60\times\pi\times AC}{180}=\frac{\pi}{3}$,解得$AC = 1$,$\therefore AD = 1$,$\therefore\triangle ACD$是等边三角形,$\therefore CD = AD$,$\angle ACD=\angle ADC = 60^{\circ}$。又$AB = 2$,$\therefore BD = 1$,$\therefore BD = CD$,$\therefore\angle B=\angle BCD = 30^{\circ}$,$\therefore\angle ACD+\angle BCD = 90^{\circ}$,即$\triangle ABC$是直角三角形,故选B。
4.新考法 如图,扇形AOB的半径为2,分别以点A、B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,两弧相交于点P,连接AB,OP,∠BOP = 35°,则$\overset{\frown}{AB}$的长 = ______.(结果保留π)(M9224013)
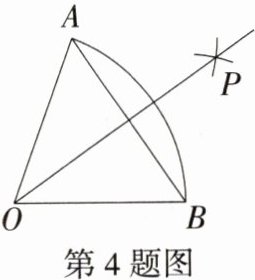

答案:
答案:$\frac{7\pi}{9}$
解析:本题借助尺规作图考查弧长计算。由作图知,$OP$垂直平分$AB$,$\because OA = OB$,$\therefore\angle AOB = 2\angle BOP = 2\times35^{\circ}=70^{\circ}$,$\because$扇形的半径是$2$,$\therefore\overset{\frown}{AB}$的长$=\frac{70\pi\times2}{180}=\frac{7\pi}{9}$。
5.如图,AB是⊙O的弦,点C是劣弧$\overset{\frown}{AB}$的中点,若∠BAC = 30°,劣弧$\overset{\frown}{AB}$的长为$\frac{2\pi}{3}$,则⊙O的半径为________.(M9224013)
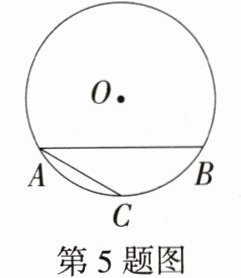

答案:
答案:$1$
解析:设$\odot O$的半径为$R$,连接$OA$、$OB$、$OC$(图略),$\because\angle BAC = 30^{\circ}$,$\therefore\angle BOC = 60^{\circ}$,$\because$点$C$是劣弧$\overset{\frown}{AB}$的中点,$\therefore\angle AOB = 120^{\circ}$,$\because$劣弧$\overset{\frown}{AB}$的长为$\frac{2\pi}{3}$,$\therefore\frac{120\pi R}{180}=\frac{2\pi}{3}$,解得$R = 1$,即$\odot O$的半径为$1$。
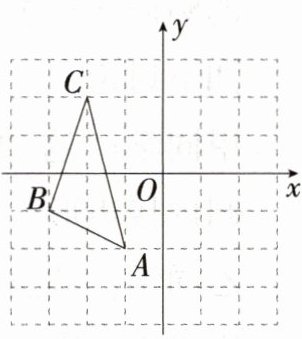
6.(2024陕西西安西工大附中模拟)如图,平面直角坐标系xOy在由边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,点A,B,C的坐标分别是(-1,-2),(-3,-1),(-2,2).
(1)把△ABC绕原点O逆时针旋转90°后得到△A'B'C',画出△A'B'C',此时A'的坐标为________.
(2)在(1)的基础上,求点B在旋转过程中运动的路径长.
(1)把△ABC绕原点O逆时针旋转90°后得到△A'B'C',画出△A'B'C',此时A'的坐标为________.
(2)在(1)的基础上,求点B在旋转过程中运动的路径长.

答案:
解析: (1)如图,$\triangle A'B'C'$即为所求,此时$A'$的坐标为$(2,-1)$。 (2)$\because OB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,$\therefore$点$B$在旋转过程中运动的路径长$=\frac{90\pi\times\sqrt{10}}{180}=\frac{\sqrt{10}\pi}{2}$。
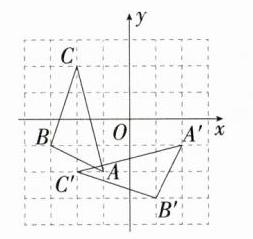
解析: (1)如图,$\triangle A'B'C'$即为所求,此时$A'$的坐标为$(2,-1)$。 (2)$\because OB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$,$\therefore$点$B$在旋转过程中运动的路径长$=\frac{90\pi\times\sqrt{10}}{180}=\frac{\sqrt{10}\pi}{2}$。

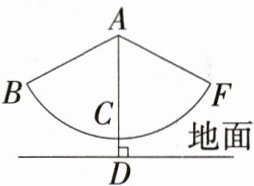
7.跨语文·诗词赏析 清代郑板桥曾有诗:“纸花如雪满天飞,娇女秋千打四围.五色罗裙风摆动,好将蝴蝶斗春归.”描写的是放风筝和荡秋千的场景.如图,秋千拉绳AB为3米,静止时踩板离地面0.5米,某人荡该秋千荡到最高处(点B)时,踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧BF的长.(M9224013)

答案:
解析:如图,过点$B$作$BG\perp AD$于$G$,$BE$垂直于地面于$E$,易知$BE = DG$,由题意知$BE = 2$,$AC = 3$,$CD = 0.5$,$\therefore AG = AD - GD = AC + CD - BE = 1.5$。$\because AB = 3$,$AG = 1.5$,$\therefore$在$Rt\triangle ABG$中,$\angle ABG = 30^{\circ}$,$\therefore\angle BAG = 60^{\circ}$,$\therefore\angle BAF = 120^{\circ}$,$\therefore$该秋千所荡过的圆弧$BF$的长为$\frac{120\times\pi\times3}{180}=2\pi$(米)。
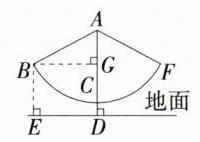
解析:如图,过点$B$作$BG\perp AD$于$G$,$BE$垂直于地面于$E$,易知$BE = DG$,由题意知$BE = 2$,$AC = 3$,$CD = 0.5$,$\therefore AG = AD - GD = AC + CD - BE = 1.5$。$\because AB = 3$,$AG = 1.5$,$\therefore$在$Rt\triangle ABG$中,$\angle ABG = 30^{\circ}$,$\therefore\angle BAG = 60^{\circ}$,$\therefore\angle BAF = 120^{\circ}$,$\therefore$该秋千所荡过的圆弧$BF$的长为$\frac{120\times\pi\times3}{180}=2\pi$(米)。

查看更多完整答案,请扫码查看


