第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
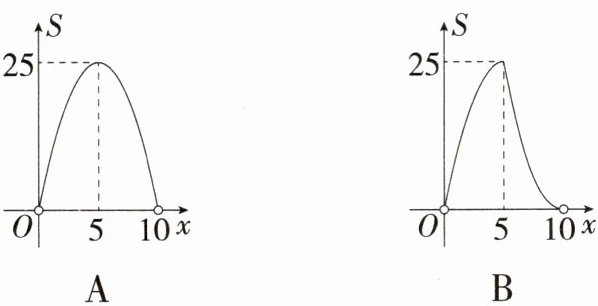
9.如图,在△ABC中,∠B = 90°,AC = 10,作△ABC的内切圆O,分别与AB、BC、AC相切于点D、E、F,设AD = x,△ABC的面积为S,则S关于x的函数图象大致为 ( )

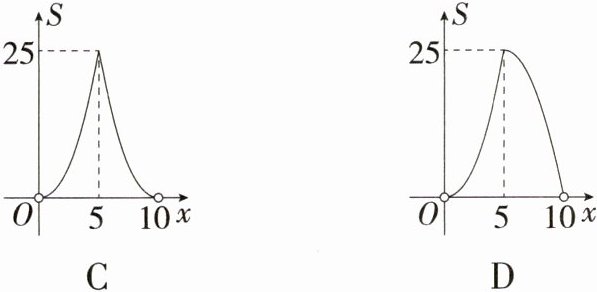


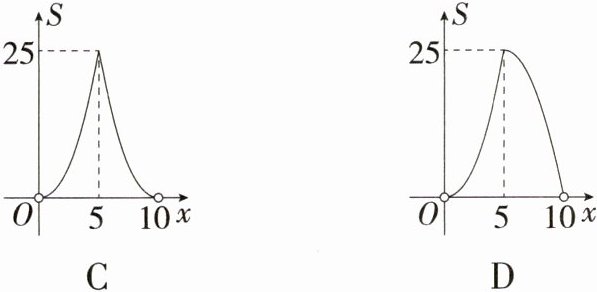
答案:
A:连接 OD、OE,如图,设⊙O 的半径为 r,因为⊙O 分别与 AB、BC、AC 相切于点 D、E、F,所以 OD ⊥ AB,OE ⊥ BC,AF = AD = x,CE = CF,所以 CE = CF = 10 - x,易得四边形 ODBE 为正方形,所以 DB = BE = OD = r,所以 S = $\frac{1}{2}r(AB + CB + AC)=\frac{1}{2}r(x + r + 10 - x + 10)=r^{2}+10r$,因为 AB² + BC² = AC²,所以(x + r)² + (10 - x + r)² = 10²,所以 r² + 10r = -x² + 10x,所以 S = -x² + 10x = -(x - 5)² + 25(0 < x < 10),故选 A。
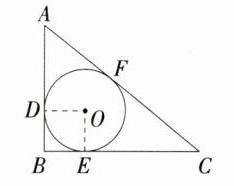
A:连接 OD、OE,如图,设⊙O 的半径为 r,因为⊙O 分别与 AB、BC、AC 相切于点 D、E、F,所以 OD ⊥ AB,OE ⊥ BC,AF = AD = x,CE = CF,所以 CE = CF = 10 - x,易得四边形 ODBE 为正方形,所以 DB = BE = OD = r,所以 S = $\frac{1}{2}r(AB + CB + AC)=\frac{1}{2}r(x + r + 10 - x + 10)=r^{2}+10r$,因为 AB² + BC² = AC²,所以(x + r)² + (10 - x + r)² = 10²,所以 r² + 10r = -x² + 10x,所以 S = -x² + 10x = -(x - 5)² + 25(0 < x < 10),故选 A。

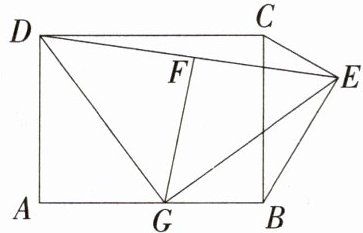
10.(2024安徽宿州宿城一中二模)如图,在矩形ABCD中,AB = 8,AD = 6,点E是BC右侧一点且CE⊥BE,点G是AB上一点,点F是DE的中点,若∠DGE = 90°,则FG的最大值为 ( )
A.$\frac{\sqrt{73}+3}{2}$
B.$\frac{\sqrt{71}+3}{2}$
C.$\frac{\sqrt{65}+4}{2}$
D.$\frac{\sqrt{61}+4}{2}$

A.$\frac{\sqrt{73}+3}{2}$
B.$\frac{\sqrt{71}+3}{2}$
C.$\frac{\sqrt{65}+4}{2}$
D.$\frac{\sqrt{61}+4}{2}$
答案:
A:因为∠DGE = 90°,点 F 是 DE 的中点,所以 FG = $\frac{1}{2}DE$,因为 CE ⊥ BE,所以∠BEC = 90°,所以点 E 在以 BC 为直径的半圆 H 上,则 H 为 BC 的中点,如图,所以当 D、H、E 在同一直线上时,DE 有最大值,此时 FG 有最大值,在矩形 ABCD 中,AB = 8,AD = 6,所以 CD = 8,CH = $\frac{1}{2}BC=\frac{1}{2}AD = 3$,所以 DH = $\sqrt{8^{2}+3^{2}}=\sqrt{73}$,HE = $\frac{1}{2}BC = 3$,所以 FG 的最大值为$\frac{1}{2}DE=\frac{\sqrt{73}+3}{2}$,故选 A。
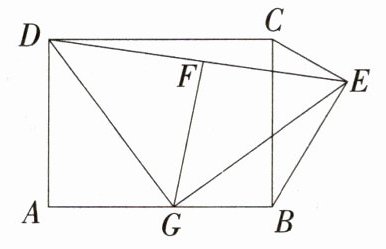
A:因为∠DGE = 90°,点 F 是 DE 的中点,所以 FG = $\frac{1}{2}DE$,因为 CE ⊥ BE,所以∠BEC = 90°,所以点 E 在以 BC 为直径的半圆 H 上,则 H 为 BC 的中点,如图,所以当 D、H、E 在同一直线上时,DE 有最大值,此时 FG 有最大值,在矩形 ABCD 中,AB = 8,AD = 6,所以 CD = 8,CH = $\frac{1}{2}BC=\frac{1}{2}AD = 3$,所以 DH = $\sqrt{8^{2}+3^{2}}=\sqrt{73}$,HE = $\frac{1}{2}BC = 3$,所以 FG 的最大值为$\frac{1}{2}DE=\frac{\sqrt{73}+3}{2}$,故选 A。

11.(2024江苏盐城中考)已知圆锥的底面半径为4,母线长为5,该圆锥的侧面积为_______.
答案:
答案:20π
解析:由圆锥的底面半径为 4,母线长为 5,可知该圆锥的侧面积为$\frac{1}{2}×2π×4×5 = 20π$。
12.新独家原创 今年五一假期期间,小清和小兰两家准备去亳州,小清和小兰要从花戏楼、曹操运兵道、亳州博物馆中选择一个景点游玩,她们各自通过抽签的方式确定景点,则两人抽到同一个景点的概率是_______.
答案:
答案:$\frac{1}{3}$ 解析:分别用 A、B、C 表示花戏楼、曹操运兵道、亳州博物馆,画树状图得:
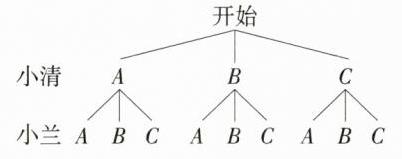
共有 9 种等可能的结果,两人抽到同一景点的情况有 3 种,则两人抽到同一景点的概率是$\frac{3}{9}=\frac{1}{3}$。
答案:$\frac{1}{3}$ 解析:分别用 A、B、C 表示花戏楼、曹操运兵道、亳州博物馆,画树状图得:

共有 9 种等可能的结果,两人抽到同一景点的情况有 3 种,则两人抽到同一景点的概率是$\frac{3}{9}=\frac{1}{3}$。
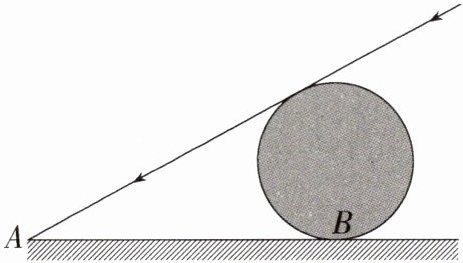
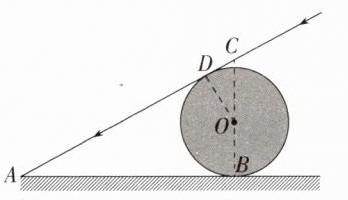
13.小明想测量一个球的半径,如图所示,在阳光下,他测得该球的影子离球的最远点A到球与地面的接触点B的距离是10米(即AB = 10米).同一时刻,他又测得竖直立在地面上长为1米的竹竿的影长为2米,那么该球的半径是_______米.

答案:
答案:(10$\sqrt{5}-20$) 解析:如图所示,设圆心为 O,易知光线与⊙O 相切,设切点为 D,连接 OD,连接 BO 并延长交直线 AD 于点 C。 根据同一时刻,阳光下物高和影长的比值相等,得$\frac{BC}{AB}=\frac{1}{2}$,所以 BC = $\frac{1}{2}AB = 5$米, 易证得 Rt△ABC∽Rt△ODC,则$\frac{AB}{OD}=\frac{AC}{OC}$。 因为 AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{10^{2}+5^{2}} = 5\sqrt{5}$(米),OC = BC - OB = BC - OD, 所以$\frac{10}{OD}=\frac{5\sqrt{5}}{5 - OD}$,所以 OD = (10$\sqrt{5}-20$)米。 故该球的半径为(10$\sqrt{5}-20$)米。
答案:(10$\sqrt{5}-20$) 解析:如图所示,设圆心为 O,易知光线与⊙O 相切,设切点为 D,连接 OD,连接 BO 并延长交直线 AD 于点 C。 根据同一时刻,阳光下物高和影长的比值相等,得$\frac{BC}{AB}=\frac{1}{2}$,所以 BC = $\frac{1}{2}AB = 5$米, 易证得 Rt△ABC∽Rt△ODC,则$\frac{AB}{OD}=\frac{AC}{OC}$。 因为 AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{10^{2}+5^{2}} = 5\sqrt{5}$(米),OC = BC - OB = BC - OD, 所以$\frac{10}{OD}=\frac{5\sqrt{5}}{5 - OD}$,所以 OD = (10$\sqrt{5}-20$)米。 故该球的半径为(10$\sqrt{5}-20$)米。

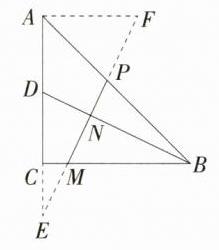
14.(2024安徽庐江模拟)如图,在△ABC中,AC = BC,∠C = 90°,点D为AC的中点,点M在BC边上,且满足$\frac{CM}{MB}=\frac{1}{5}$,MP⊥BD,垂足为N,交AB于点P.
(1)cos∠DBC的值为_______.
(2)$\frac{AP}{PB}$的值为_______.

(1)cos∠DBC的值为_______.
(2)$\frac{AP}{PB}$的值为_______.

答案:
答案:
(1)$\frac{2\sqrt{5}}{5}$
(2)$\frac{4}{5}$ 解析:设 CM = a,则 BM = 5a,所以 BC = CM + BM = 6a,因为 AC = BC,所以 AC = 6a,因为点 D 为 AC 的中点,所以 CD = 3a。
(1)因为∠C = 90°,所以 BD = $\sqrt{BC^{2}+CD^{2}} = 3\sqrt{5}a$,所以 cos∠DBC = $\frac{BC}{BD}=\frac{6a}{3\sqrt{5}a}=\frac{2\sqrt{5}}{5}$。
(2)如图,延长 PM,交 AC 的延长线于点 E,过点 A 作 AF//BC 交 MP 的延长线于点 F, 因为∠ACB = 90°,MP ⊥ BD 于 N,所以∠BDC + ∠DBC = 90°,∠BDC + ∠E = 90°,所以∠DBC = ∠E, 又因为∠ECM = ∠BCD = 90°,所以△EMC∽△BDC,所以$\frac{CE}{CB}=\frac{CM}{CD}$,$\frac{CE}{6a}=\frac{a}{3a}$,所以 CE = 2a, 因为 AF//BC,所以△ECM∽△EAF,△AFP∽△BMP,所以$\frac{CM}{AF}=\frac{CE}{AE}=\frac{2a}{2a + 6a}=\frac{1}{4}$,$\frac{AP}{BP}=\frac{AF}{BM}$,所以 AF = 4a,所以$\frac{AP}{BP}=\frac{4a}{5a}=\frac{4}{5}$。
答案:
(1)$\frac{2\sqrt{5}}{5}$
(2)$\frac{4}{5}$ 解析:设 CM = a,则 BM = 5a,所以 BC = CM + BM = 6a,因为 AC = BC,所以 AC = 6a,因为点 D 为 AC 的中点,所以 CD = 3a。
(1)因为∠C = 90°,所以 BD = $\sqrt{BC^{2}+CD^{2}} = 3\sqrt{5}a$,所以 cos∠DBC = $\frac{BC}{BD}=\frac{6a}{3\sqrt{5}a}=\frac{2\sqrt{5}}{5}$。
(2)如图,延长 PM,交 AC 的延长线于点 E,过点 A 作 AF//BC 交 MP 的延长线于点 F, 因为∠ACB = 90°,MP ⊥ BD 于 N,所以∠BDC + ∠DBC = 90°,∠BDC + ∠E = 90°,所以∠DBC = ∠E, 又因为∠ECM = ∠BCD = 90°,所以△EMC∽△BDC,所以$\frac{CE}{CB}=\frac{CM}{CD}$,$\frac{CE}{6a}=\frac{a}{3a}$,所以 CE = 2a, 因为 AF//BC,所以△ECM∽△EAF,△AFP∽△BMP,所以$\frac{CM}{AF}=\frac{CE}{AE}=\frac{2a}{2a + 6a}=\frac{1}{4}$,$\frac{AP}{BP}=\frac{AF}{BM}$,所以 AF = 4a,所以$\frac{AP}{BP}=\frac{4a}{5a}=\frac{4}{5}$。

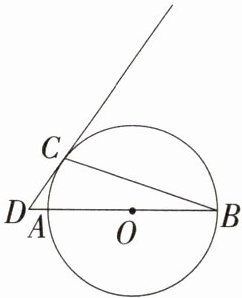
15.[答案含评分细则](6分)如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作⊙O的切线交BA的延长线于点D,若∠D = 54°,求∠B的度数.

答案:
解析:连接 OC(图略),
因为 DC 为⊙O 的切线,所以 OC ⊥ CD,所以∠OCD = 90°,
因为∠D = 54°,所以∠COD = 90° - ∠D = 36°,
所以∠B = $\frac{1}{2}∠COD = 18°$。
查看更多完整答案,请扫码查看


