第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
19.(6分)如图,在一不规则区域内,有一边长为3$\sqrt{3}$米的正方形,向区域内随机地撒4 000粒黄豆,数得落在正方形区域内(含边界)的黄豆有1 350粒,以此实验数据为依据,可以估计出该不规则区域的面积.
(1)随机向不规则区域内掷一粒黄豆,求黄豆落在正方形区域内(含边界)的概率.
(2)请你估计出该不规则区域的面积.
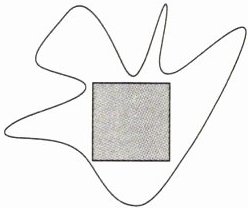
(1)随机向不规则区域内掷一粒黄豆,求黄豆落在正方形区域内(含边界)的概率.
(2)请你估计出该不规则区域的面积.

答案:
(1)记“黄豆落在正方形区域内”为事件A,
∴P(A) = $\frac{1350}{4000}=\frac{27}{80}$。 故黄豆落在正方形区域内(含边界)的概率为$\frac{27}{80}$。 (2)
∵P = $\frac{27}{80}$,正方形区域的面积 = $(3\sqrt{3})^{2}=27$平方米,
∴估计不规则区域的面积为27÷$\frac{27}{80}$ = 80平方米。
∴P(A) = $\frac{1350}{4000}=\frac{27}{80}$。 故黄豆落在正方形区域内(含边界)的概率为$\frac{27}{80}$。 (2)
∵P = $\frac{27}{80}$,正方形区域的面积 = $(3\sqrt{3})^{2}=27$平方米,
∴估计不规则区域的面积为27÷$\frac{27}{80}$ = 80平方米。
20.(7分)甲、乙两人分别在道路的A、B两处.
(1)如图①,若两人“向东”或“向西”随机运动,求两人“相向而行”的概率.
(2)如图②,若两人在“十”形道路上“向东”“向西”“向南”“向北”随机运动,已知甲的速度比乙快,求两人“不会相遇”的概率.

(1)如图①,若两人“向东”或“向西”随机运动,求两人“相向而行”的概率.
(2)如图②,若两人在“十”形道路上“向东”“向西”“向南”“向北”随机运动,已知甲的速度比乙快,求两人“不会相遇”的概率.

答案:
(1)根据题意知,两人的运动方向共有4种情况,且每种情况发生的可能性相同,而相向而行的情况只有1种,所以两人“相向而行”的概率为$\frac{1}{4}$。 (2)画树状图如下:
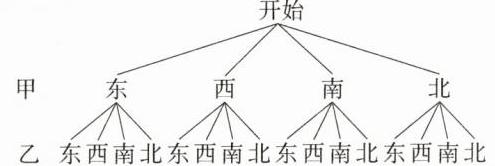
由树状图知共有16种等可能的情况,其中相遇的情况只有“相向而行”和“两人都向东”这2种,所以两人“不会相遇”的概率为$\frac{16 - 2}{16}=\frac{7}{8}$。
(1)根据题意知,两人的运动方向共有4种情况,且每种情况发生的可能性相同,而相向而行的情况只有1种,所以两人“相向而行”的概率为$\frac{1}{4}$。 (2)画树状图如下:

由树状图知共有16种等可能的情况,其中相遇的情况只有“相向而行”和“两人都向东”这2种,所以两人“不会相遇”的概率为$\frac{16 - 2}{16}=\frac{7}{8}$。
21.(2023江苏常州中考)(7分)在5张相同的小纸条上分别写有①$\sqrt{2}$;②$\sqrt{8}$;③1;④乘法;⑤加法.将这5张小纸条做成5支签,①②③放在不透明的盒子A中搅匀,④⑤放在不透明的盒子B中搅匀.
(1)从盒子A中任意抽出1支签,抽到无理数的概率是________.
(2)先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签.求抽到的2个实数进行相应的运算后结果是无理数的概率.
(1)从盒子A中任意抽出1支签,抽到无理数的概率是________.
(2)先从盒子A中任意抽出2支签,再从盒子B中任意抽出1支签.求抽到的2个实数进行相应的运算后结果是无理数的概率.
答案:
(1)①$\sqrt{2}$;②$\sqrt{8}$;③1中,无理数有2个,
∴从盒子A中任意抽出1支签,抽到无理数的概率是$\frac{2}{3}$。 (2)画树状图如图所示
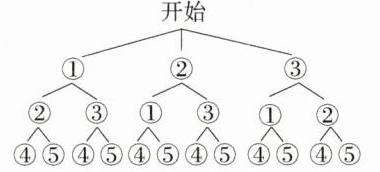
共有12种等可能的情况,其中抽到的2个实数进行相应的运算后结果是无理数的情况有①②⑤,①③④,①③⑤,②①⑤,②③④,②③⑤,③①④,③①⑤,③②④,③②⑤,共10种,
∴抽到的2个实数进行相应的运算后结果是无理数的概率为$\frac{10}{12}=\frac{5}{6}$。
(1)①$\sqrt{2}$;②$\sqrt{8}$;③1中,无理数有2个,
∴从盒子A中任意抽出1支签,抽到无理数的概率是$\frac{2}{3}$。 (2)画树状图如图所示

共有12种等可能的情况,其中抽到的2个实数进行相应的运算后结果是无理数的情况有①②⑤,①③④,①③⑤,②①⑤,②③④,②③⑤,③①④,③①⑤,③②④,③②⑤,共10种,
∴抽到的2个实数进行相应的运算后结果是无理数的概率为$\frac{10}{12}=\frac{5}{6}$。
查看更多完整答案,请扫码查看


