第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
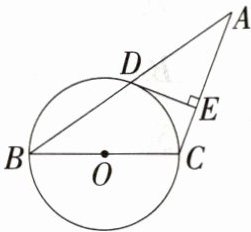
8.[教材变式·P40T5](2024吉林蛟河期末)如图,在△ABC中,AC = BC,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.求证:DE为⊙O的切线.(M9224009)

答案:
证明:连接OD,如图。因为AC = BC,所以∠A = ∠ABC,因为OB = OD,所以∠ODB = ∠ABC,所以∠ODB = ∠A,所以OD//AC,又因为DE⊥AC,所以DE⊥OD,因为OD为⊙O的半径,所以DE为⊙O的切线。
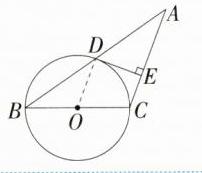
证明:连接OD,如图。因为AC = BC,所以∠A = ∠ABC,因为OB = OD,所以∠ODB = ∠ABC,所以∠ODB = ∠A,所以OD//AC,又因为DE⊥AC,所以DE⊥OD,因为OD为⊙O的半径,所以DE为⊙O的切线。

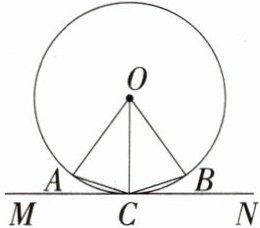
9.(2024福建中考,7,★★☆)如图,已知点A,B在⊙O上,∠AOB = 72°,直线MN与⊙O相切,切点为C,且C为$\overset{\frown}{AB}$的中点,则∠ACM等于 ( )
A.18°
B.30°
C.36°
D.72°

A.18°
B.30°
C.36°
D.72°
答案:
A:因为C为$\overset{\frown}{AB}$的中点,∠AOB = 72°,所以∠AOC = ∠BOC = 36°。因为OA = OC,所以∠ACO = ∠OAC = 72°。因为直线MN与⊙O相切,切点为C,所以∠OCM = 90°,所以∠ACM = ∠OCM - ∠ACO = 90° - 72° = 18°,故选A。
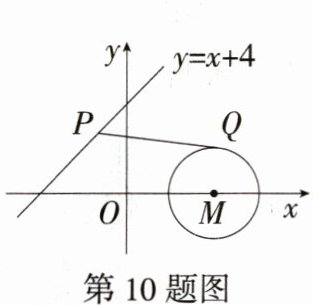
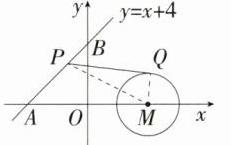
10.[线段最值问题](2024四川凉山州中考,24,★★☆)如图,⊙M的圆心为M(4,0),半径为2,P是直线y = x + 4上的一个动点,过点P作⊙M的切线,切点为Q,则PQ的最小值为__________. (M9224009)

答案:
答案:2$\sqrt{7}$ 解析:如图,连接MP、MQ,因为PQ是⊙M的切线,所以MQ⊥PQ,所以PQ = $\sqrt{PM^{2}-MQ^{2}}=\sqrt{PM^{2}-4}$,当PM最小时,PQ最小,当MP⊥AB时,MP最小,直线y = x + 4与x轴的交点A的坐标为(-4,0),与y轴的交点B的坐标为(0,4),所以OA = OB = 4,AM = 8,所以∠BAO = 45°,当MP⊥AB时,MP = AM·sin∠BAO = 8×$\frac{\sqrt{2}}{2}=4\sqrt{2}$,所以PQ的最小值为$\sqrt{(4\sqrt{2})^{2}-4}=\sqrt{28}=2\sqrt{7}$。
答案:2$\sqrt{7}$ 解析:如图,连接MP、MQ,因为PQ是⊙M的切线,所以MQ⊥PQ,所以PQ = $\sqrt{PM^{2}-MQ^{2}}=\sqrt{PM^{2}-4}$,当PM最小时,PQ最小,当MP⊥AB时,MP最小,直线y = x + 4与x轴的交点A的坐标为(-4,0),与y轴的交点B的坐标为(0,4),所以OA = OB = 4,AM = 8,所以∠BAO = 45°,当MP⊥AB时,MP = AM·sin∠BAO = 8×$\frac{\sqrt{2}}{2}=4\sqrt{2}$,所以PQ的最小值为$\sqrt{(4\sqrt{2})^{2}-4}=\sqrt{28}=2\sqrt{7}$。

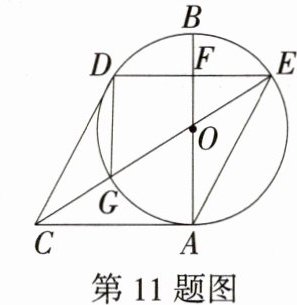
11.(2024重庆中考A卷,17,★★☆)如图,以AB为直径的⊙O与AC相切于点A,以AC为边作平行四边形ACDE,点D,E均在⊙O上,DE与AB交于点F,连接CE,与⊙O交于点G,连接DG.若AB = 10,DE = 8,则AF = __________,DG = __________.

答案:
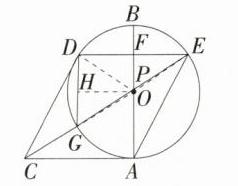
答案:8;$\frac{20\sqrt{13}}{13}$ 解析:连接OE、OD、OG,过O点作OH⊥DG于H点,CE交AF于P点,如图,因为以AB为直径的⊙O与AC相切于点A,所以AB⊥AC。因为四边形ACDE为平行四边形,所以AC//DE,AC = DE = 8,所以AB⊥DE,所以DF = EF = $\frac{1}{2}$DE = 4。因为AB = 10,所以OA = OE = 5。在Rt△OEF中,OF = $\sqrt{OE^{2}-EF^{2}}=\sqrt{5^{2}-4^{2}} = 3$,所以AF = OA + OF = 5 + 3 = 8。因为DE//AC,所以$\frac{FP}{PA}=\frac{EF}{AC}=\frac{1}{2}$,∠DEG = ∠PCA,所以PA = $\frac{2}{3}\times8=\frac{16}{3}$,在Rt△ACP中,PC = $\sqrt{8^{2}+(\frac{16}{3})^{2}}=\frac{8\sqrt{13}}{3}$。因为∠DOG = 2∠DEG,∠DOG = 2∠DOH,所以∠DEG = ∠DOH,所以∠DOH = ∠PCA,所以Rt△DOH∽Rt△PCA,所以DH : PA = OD : PC,即DH : $\frac{16}{3}=5:\frac{8\sqrt{13}}{3}$,所以DH = $\frac{10\sqrt{13}}{13}$。因为OH⊥DG,所以DG = 2DH = $\frac{20\sqrt{13}}{13}$。
答案:8;$\frac{20\sqrt{13}}{13}$ 解析:连接OE、OD、OG,过O点作OH⊥DG于H点,CE交AF于P点,如图,因为以AB为直径的⊙O与AC相切于点A,所以AB⊥AC。因为四边形ACDE为平行四边形,所以AC//DE,AC = DE = 8,所以AB⊥DE,所以DF = EF = $\frac{1}{2}$DE = 4。因为AB = 10,所以OA = OE = 5。在Rt△OEF中,OF = $\sqrt{OE^{2}-EF^{2}}=\sqrt{5^{2}-4^{2}} = 3$,所以AF = OA + OF = 5 + 3 = 8。因为DE//AC,所以$\frac{FP}{PA}=\frac{EF}{AC}=\frac{1}{2}$,∠DEG = ∠PCA,所以PA = $\frac{2}{3}\times8=\frac{16}{3}$,在Rt△ACP中,PC = $\sqrt{8^{2}+(\frac{16}{3})^{2}}=\frac{8\sqrt{13}}{3}$。因为∠DOG = 2∠DEG,∠DOG = 2∠DOH,所以∠DEG = ∠DOH,所以∠DOH = ∠PCA,所以Rt△DOH∽Rt△PCA,所以DH : PA = OD : PC,即DH : $\frac{16}{3}=5:\frac{8\sqrt{13}}{3}$,所以DH = $\frac{10\sqrt{13}}{13}$。因为OH⊥DG,所以DG = 2DH = $\frac{20\sqrt{13}}{13}$。

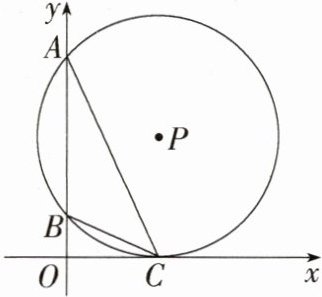
12.[新考法](2023山东威海中考,21,★★☆)如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连接AC,BC.(M9224009)
(1)求点P的坐标.
(2)求cos∠ACB的值.
(1)求点P的坐标.
(2)求cos∠ACB的值.

答案:
解析:本题以平面直角坐标系为背景,考查切线的性质和圆的性质。 (1)如图,连接PC,PB。因为点A(0,8),B(0,2),所以AB = 6。过P作PH⊥AB于H,所以AH = BH = 3,所以OH = 5。因为⊙P与x轴相切于点C,所以PC⊥x轴。易知四边形OHPC为矩形,所以PC = OH = 5,所以PB = 5。所以PH = $\sqrt{PB^{2}-BH^{2}} = 4$,所以点P的坐标为(4,5)。 (2)如图,连接AP并延长交⊙P于M,连接BM,则∠ABM = 90°。在Rt△ABM中,BM = $\sqrt{AM^{2}-AB^{2}}=\sqrt{10^{2}-6^{2}} = 8$。所以cos∠ACB = cos∠AMB = $\frac{BM}{AM}=\frac{8}{10}=\frac{4}{5}$。
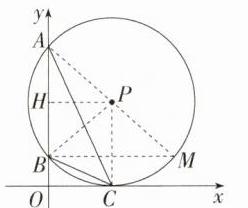
解析:本题以平面直角坐标系为背景,考查切线的性质和圆的性质。 (1)如图,连接PC,PB。因为点A(0,8),B(0,2),所以AB = 6。过P作PH⊥AB于H,所以AH = BH = 3,所以OH = 5。因为⊙P与x轴相切于点C,所以PC⊥x轴。易知四边形OHPC为矩形,所以PC = OH = 5,所以PB = 5。所以PH = $\sqrt{PB^{2}-BH^{2}} = 4$,所以点P的坐标为(4,5)。 (2)如图,连接AP并延长交⊙P于M,连接BM,则∠ABM = 90°。在Rt△ABM中,BM = $\sqrt{AM^{2}-AB^{2}}=\sqrt{10^{2}-6^{2}} = 8$。所以cos∠ACB = cos∠AMB = $\frac{BM}{AM}=\frac{8}{10}=\frac{4}{5}$。

13.(2024四川南充中考,22,★★☆)如图,在⊙O中,AB是直径,AE是弦,点F是$\overset{\frown}{AE}$上一点,$\overset{\frown}{AF}$ = $\overset{\frown}{BE}$,AE,BF交于点C,点D为BF延长线上一点,且∠CAD = ∠CDA.
(1)求证:AD是⊙O的切线.
(2)若BE = 4,AD = 2$\sqrt{5}$,求⊙O的半径.
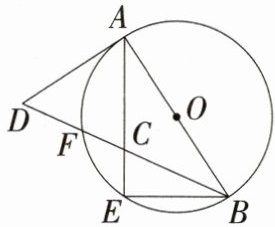
(1)求证:AD是⊙O的切线.
(2)若BE = 4,AD = 2$\sqrt{5}$,求⊙O的半径.

答案:
解析: (1)证明:因为$\overset{\frown}{AF}=\overset{\frown}{BE}$,所以∠ABF = ∠BAE。因为∠CAD + ∠BAE + ∠CDA + ∠ABF = 180°,且∠CAD = ∠CDA,所以∠CAD + ∠BAE + ∠CAD + ∠BAE = 180°,所以∠OAD = ∠CAD + ∠BAE = 90°。因为OA是⊙O的半径且AD⊥OA,所以AD是⊙O的切线。 (2)如图,连接AF。因为$\overset{\frown}{AF}=\overset{\frown}{BE}$,BE = 4,所以AF = BE = 4。因为AB是⊙O的直径,所以∠AFD = ∠AFB = 90°,所以DF = $\sqrt{AD^{2}-AF^{2}}=\sqrt{(2\sqrt{5})^{2}-4^{2}} = 2$。因为∠BAD = ∠AFD = 90°,所以$\frac{AB}{AD}=\frac{AF}{DF}=\tan D=\frac{4}{2}=2$,所以AD = $\frac{1}{2}$AB,所以OA = $\frac{1}{2}$AB = AD = 2$\sqrt{5}$,所以⊙O的半径长为2$\sqrt{5}$。
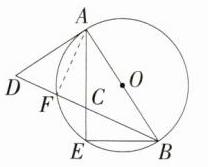
解析: (1)证明:因为$\overset{\frown}{AF}=\overset{\frown}{BE}$,所以∠ABF = ∠BAE。因为∠CAD + ∠BAE + ∠CDA + ∠ABF = 180°,且∠CAD = ∠CDA,所以∠CAD + ∠BAE + ∠CAD + ∠BAE = 180°,所以∠OAD = ∠CAD + ∠BAE = 90°。因为OA是⊙O的半径且AD⊥OA,所以AD是⊙O的切线。 (2)如图,连接AF。因为$\overset{\frown}{AF}=\overset{\frown}{BE}$,BE = 4,所以AF = BE = 4。因为AB是⊙O的直径,所以∠AFD = ∠AFB = 90°,所以DF = $\sqrt{AD^{2}-AF^{2}}=\sqrt{(2\sqrt{5})^{2}-4^{2}} = 2$。因为∠BAD = ∠AFD = 90°,所以$\frac{AB}{AD}=\frac{AF}{DF}=\tan D=\frac{4}{2}=2$,所以AD = $\frac{1}{2}$AB,所以OA = $\frac{1}{2}$AB = AD = 2$\sqrt{5}$,所以⊙O的半径长为2$\sqrt{5}$。

查看更多完整答案,请扫码查看


