《2025年5年中考3年模拟九年级数学下册沪科版》

1. 与圆心的距离不大于半径的点所组成的图形是（ ）
A. 圆的外部(包括边界)
B. 圆的内部(不包括边界)
C. 圆
D. 圆的内部(包括边界)

答案： D 与圆心的距离不大于半径的点在圆上或圆的内部，故选D.

2. 情境题·数学文化 (2024吉林松原宁江期末)《墨经》中有“圆，一中同长也”的记载，这句话里“中”字可以理解为________.

答案： 答案 圆心 解析 “圆，一中同长也”，表示圆心到圆上各点的距离都相等，即半径都相等，故答案为圆心.

3. 新考法 (2023广西柳州柳南一模改编)已知⊙O的半径为3，OA = 2，则下列四个图形中，正确的是（M9224005）（ ）

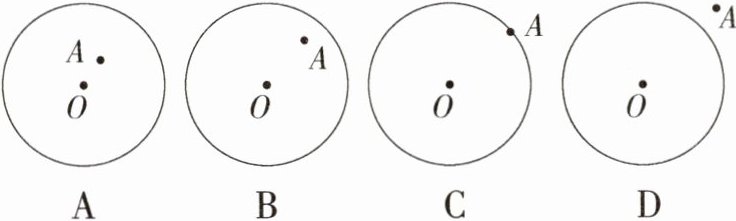
答案： B 本题将点与圆的位置关系用图形展示出来，考查形式比较新颖.
∵ ⊙O的半径为3，OA = 2，
∴ 点A在⊙O内且点A靠近圆的边界，故选B.

4. 新独家原创 如图，在矩形ABCD中，AB = 4，BC = 3，以点A为圆心，4为半径画圆，则B，C，D三点，在圆内的是点________，在圆外的是点________，在圆上的是点________. 若以点A为圆心作圆，点B、C、D至少有一点在圆内，且至少有一点在圆外，那么⊙A的半径r的取值范围是________.（M9224005）

答案： 答案 D；C；B；3＜r＜5 解析
∵ 在矩形ABCD中，AB = 4，BC = 3，
∴ AC = $\sqrt{3^{2}+4^{2}}$ = 5.
∵ AD = BC = 3＜4，
∴ 点D在圆内.
∵ AB = 4，
∴ 点B在圆上.
∵ AC = 5＞4，
∴ 点C在圆外.
∵ 点B、C、D至少有一点在圆内，
∴ r＞3；
∵ 点B、C、D至少有一点在圆外，
∴ r＜5.综上所述，r的取值范围是3＜r＜5.

5. 教材变式·P14T3 如图，在四边形ABCD中，∠A = ∠C = 90°. 求证：A，B，C，D四个点在同一个圆上.

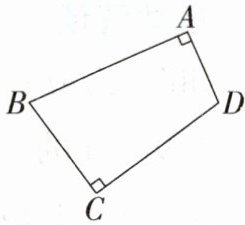
答案：
证明 如图，连接BD，取BD的中点O，连接OA，OC.

∵ ∠BAD = ∠BCD = 90°，OB = OD，
∴ OA = OB = OD = OC，
∴ A，B，C，D四个点在同一个圆上. ·方法归纳 根据圆的定义可知，如果几个点到点O的距离相等，那么这几个点在以点O为圆心，点O到这几个点的距离为半径的圆上.

6. (2024黑龙江绥化期末)下列说法：①弦是直径；②半圆是弧；③过圆心的线段是直径；④圆心相同且半径相同的两个圆是同心圆. 其中错误的有（M9224005）（ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： C 连接圆上任意两点的线段叫做弦，其中，经过圆心的弦叫做直径，而过圆心的线段不一定是弦，故过圆心的线段不一定是直径，③错误；直径是弦，但弦不一定是直径，①错误；圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆，所以半圆是弧，②正确；④圆心相同半径不同的两个圆是同心圆，④错误. 故选C.

7. 新独家原创 如图，点A，B，C，D，E都在⊙O上，且圆心O是AB、CD的交点，则图中共有________条弦，分别是________. 这些弦中，直径是________. 以点A为端点的优弧是________，若点A是$\overset{\frown}{DE}$的中点，则相等的劣弧是________.（M9224005）

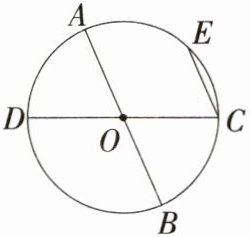
答案： 答案 3；AB，CD，CE；AB，CD；$\overset{\frown}{ABC}$，$\overset{\frown}{ABE}$，$\overset{\frown}{ABD}$；$\overset{\frown}{AD}$，$\overset{\frown}{AE}$ 解析 根据圆的有关概念，题图中共有AB，CD，CE三条弦，其中AB、CD经过圆心，是直径. 以点A为端点的优弧是$\overset{\frown}{ABC}$，$\overset{\frown}{ABE}$，$\overset{\frown}{ABD}$.
∵ 点A是$\overset{\frown}{DE}$的中点，
∴ 相等的劣弧是$\overset{\frown}{AD}$，$\overset{\frown}{AE}$.

8. 整体思想 如图，△ABC的三个顶点A，B，C都在⊙O上，圆心O在边AB上. 求证：△ABC是直角三角形.

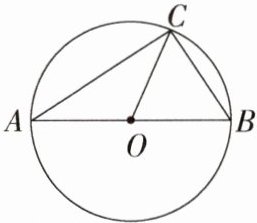
答案： 证明
∵ 点A，B，C都在⊙O上，且点O在AB上，
∴ OA = OB = OC，
∴ ∠A = ∠ACO，∠B = ∠BCO.
∵ ∠A+∠B+∠ACB = 180°，∠ACB = ∠ACO+∠BCO，
∴ ∠A+∠B+(∠A+∠B) = 180°，即∠A+∠B = 0°，
∴ ∠ACB = 90°，
∴ △ABC是直角三角形. ·方法解读 整体思想是在研究和解决有关数学问题时，把某些式子或图形看成一个整体，通过研究问题的整体形式、整体结构、整体特征，从而对问题进行整体处理的思想思想. 本题中将∠A+∠B看作一个整体进而求出结果.