第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
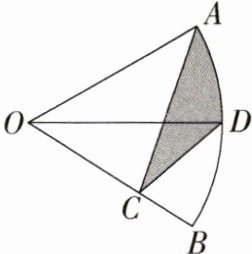
9.推理能力 动点最值问题(2023内蒙古通辽中考)如图,在扇形AOB中,∠AOB = 60°,OD平分∠AOB交$\overset{\frown}{AB}$于点D,点C是半径OB上一动点,若OA = 1,则阴影部分周长的最小值为 ( )
A.$\sqrt{2}$ + $\frac{\pi}{6}$
B.$\sqrt{2}$ + $\frac{\pi}{3}$
C.2$\sqrt{2}$ + $\frac{\pi}{6}$
D.2$\sqrt{2}$ + $\frac{\pi}{3}$

A.$\sqrt{2}$ + $\frac{\pi}{6}$
B.$\sqrt{2}$ + $\frac{\pi}{3}$
C.2$\sqrt{2}$ + $\frac{\pi}{6}$
D.2$\sqrt{2}$ + $\frac{\pi}{3}$
答案:
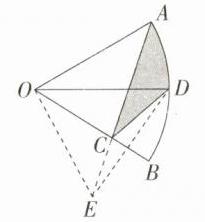
A 如图,作D点关于直线OB的对称点E,连接AE,与OB的交点为C,此时阴影部分的周长最小,连接OE,在扇形AOB中,∠AOB = 60°,OD平分∠AOB交$\overset{\frown}{AB}$于点D,
∴ ∠AOD = ∠BOD = 30°,由轴对称的性质,得∠EOB = ∠BOD = 30°,OE = OD,CD = CE,
∴ ∠AOE = 90°,
∴ △AOE是等腰直角三角形,
∵ OA = 1,
∴ AE = $\sqrt{2}$,$\overset{\frown}{AD}$的长 = $\frac{30π×1}{180}$ = $\frac{π}{6}$,
∴ 阴影部分周长的最小值为$\sqrt{2}$ + $\frac{π}{6}$,故选A.
A 如图,作D点关于直线OB的对称点E,连接AE,与OB的交点为C,此时阴影部分的周长最小,连接OE,在扇形AOB中,∠AOB = 60°,OD平分∠AOB交$\overset{\frown}{AB}$于点D,
∴ ∠AOD = ∠BOD = 30°,由轴对称的性质,得∠EOB = ∠BOD = 30°,OE = OD,CD = CE,
∴ ∠AOE = 90°,
∴ △AOE是等腰直角三角形,
∵ OA = 1,
∴ AE = $\sqrt{2}$,$\overset{\frown}{AD}$的长 = $\frac{30π×1}{180}$ = $\frac{π}{6}$,
∴ 阴影部分周长的最小值为$\sqrt{2}$ + $\frac{π}{6}$,故选A.

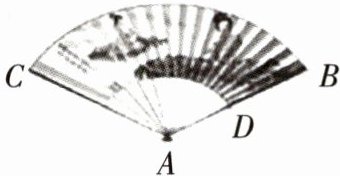
10.模型观念 新考向·教材拓展探究试题 【教材原题】如图,一折扇完全打开后,若外侧两竹片AB,AC的夹角为120°,AB长为25 cm,贴纸部分BD长为14 cm,则贴纸部分的面积(双面)为多少?
【解答过程】两面贴纸部分的面积S = 2×$(\frac{120\pi×25^{2}}{360}-\frac{120\pi×11^{2}}{360})$ = 336π(cm²).
【问题分析】纸扇是由圆心角相同,半径不同的两个扇形组成的,本题已知的三个条件为扇形的圆心角和两个扇形的半径.
【拓展探究】
(1)如图1,一折扇完全打开后,若外侧两竹片AB,AC的夹角为120°,$l_{\overset{\frown}{BC}}$ = 20π cm,$l_{\overset{\frown}{DE}}$ = $\frac{20}{3}\pi$ cm,求扇面的面积.
【形成规律】
(2)如图1,一折扇完全打开后,若BD的长为h cm,$l_{\overset{\frown}{BC}}$ = m cm,$l_{\overset{\frown}{DE}}$ = n cm,求证:扇面的面积S = $\frac{1}{2}$(m + n)h cm².
【问题延伸】
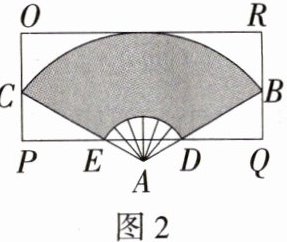
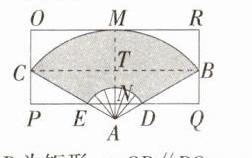
(3)如图2,若要从矩形OPQR中剪出符合第(1)问题干中要求的扇面BDEC,求矩形OPQR的长与宽的最小值.

【解答过程】两面贴纸部分的面积S = 2×$(\frac{120\pi×25^{2}}{360}-\frac{120\pi×11^{2}}{360})$ = 336π(cm²).
【问题分析】纸扇是由圆心角相同,半径不同的两个扇形组成的,本题已知的三个条件为扇形的圆心角和两个扇形的半径.
【拓展探究】
(1)如图1,一折扇完全打开后,若外侧两竹片AB,AC的夹角为120°,$l_{\overset{\frown}{BC}}$ = 20π cm,$l_{\overset{\frown}{DE}}$ = $\frac{20}{3}\pi$ cm,求扇面的面积.
【形成规律】
(2)如图1,一折扇完全打开后,若BD的长为h cm,$l_{\overset{\frown}{BC}}$ = m cm,$l_{\overset{\frown}{DE}}$ = n cm,求证:扇面的面积S = $\frac{1}{2}$(m + n)h cm².
【问题延伸】
(3)如图2,若要从矩形OPQR中剪出符合第(1)问题干中要求的扇面BDEC,求矩形OPQR的长与宽的最小值.



答案:
解析 \n(1)
∵ $l_{\overset{\frown}{BC}}$ = $\frac{120π\cdot AB}{180}$ = 20π cm,
∴ AB = 30 cm,
∵ $l_{\overset{\frown}{DE}}$ = $\frac{120π\cdot AD}{180}$ = $\frac{20}{3}$π cm,
∴ AD = 10 cm,
∴ S = $S_{扇形BAC}$ - $S_{扇形DAE}$ = $\frac{120π\cdot AB^{2}}{360}$ - $\frac{120π\cdot AD^{2}}{360}$ = $\frac{120π}{360}$($AB^{2}-AD^{2}$) = $\frac{120π}{360}$×($30^{2}-10^{2}$) = $\frac{800π}{3}$(cm²).\n(2)证明:设∠BAC = x°,
∵ $l_{\overset{\frown}{BC}}$ = $\frac{xπ\cdot AB}{180}$ = m cm,
∴ AB = $\frac{180m}{xπ}$ cm,
∵ $l_{\overset{\frown}{DE}}$ = $\frac{xπ\cdot AD}{180}$ = n cm,
∴ AD = $\frac{180n}{xπ}$ cm,
∴ S = $S_{扇形BAC}$ - $S_{扇形DAE}$ = $\frac{xπ\cdot AB^{2}}{360}$ - $\frac{xπ\cdot AD^{2}}{360}$ = $\frac{xπ}{360}$($AB^{2}-AD^{2}$) = $\frac{xπ}{360}$(AB + AD)(AB - AD),
∵ AB - AD = BD = h cm,
∴ S = $\frac{xπ}{360}$($\frac{180m}{xπ}$ + $\frac{180n}{xπ}$)h = $\frac{1}{2}$(m + n)h cm².\n(3)连接BC,过点A作AN⊥DE于N,延长AN交BC于T,交OR于M,如图.
∵ 四边形OPQR为矩形,
∴ OR//PQ. 由题意得OR//PQ//BC,OR = PQ = BC,
∵ AN⊥DE,
∴ AM⊥OR,AT⊥BC,
∴ OR = BC = 2BT.
∵ ∠BAC = 120°,
∴ ∠BAM = 60°,
∴ ∠ADN = ∠ABT = 30°. 由(1)知,AB = 30 cm,AD = 10 cm,
∴ AN = $\frac{1}{2}$AD = 5 cm,AT = $\frac{1}{2}$AB = 15 cm,
∴ MN = AM - AN = AB - AN = 25 cm,BT = $\sqrt{AB^{2}-AT^{2}}$ = $15\sqrt{3}$ cm,
∴ OR = 2BT = $30\sqrt{3}$ cm,OP = MN = 25 cm,
∴ 矩形OPQR的长与宽的最小值分别为$30\sqrt{3}$ cm和25 cm.
解析 \n(1)
∵ $l_{\overset{\frown}{BC}}$ = $\frac{120π\cdot AB}{180}$ = 20π cm,
∴ AB = 30 cm,
∵ $l_{\overset{\frown}{DE}}$ = $\frac{120π\cdot AD}{180}$ = $\frac{20}{3}$π cm,
∴ AD = 10 cm,
∴ S = $S_{扇形BAC}$ - $S_{扇形DAE}$ = $\frac{120π\cdot AB^{2}}{360}$ - $\frac{120π\cdot AD^{2}}{360}$ = $\frac{120π}{360}$($AB^{2}-AD^{2}$) = $\frac{120π}{360}$×($30^{2}-10^{2}$) = $\frac{800π}{3}$(cm²).\n(2)证明:设∠BAC = x°,
∵ $l_{\overset{\frown}{BC}}$ = $\frac{xπ\cdot AB}{180}$ = m cm,
∴ AB = $\frac{180m}{xπ}$ cm,
∵ $l_{\overset{\frown}{DE}}$ = $\frac{xπ\cdot AD}{180}$ = n cm,
∴ AD = $\frac{180n}{xπ}$ cm,
∴ S = $S_{扇形BAC}$ - $S_{扇形DAE}$ = $\frac{xπ\cdot AB^{2}}{360}$ - $\frac{xπ\cdot AD^{2}}{360}$ = $\frac{xπ}{360}$($AB^{2}-AD^{2}$) = $\frac{xπ}{360}$(AB + AD)(AB - AD),
∵ AB - AD = BD = h cm,
∴ S = $\frac{xπ}{360}$($\frac{180m}{xπ}$ + $\frac{180n}{xπ}$)h = $\frac{1}{2}$(m + n)h cm².\n(3)连接BC,过点A作AN⊥DE于N,延长AN交BC于T,交OR于M,如图.
∵ 四边形OPQR为矩形,
∴ OR//PQ. 由题意得OR//PQ//BC,OR = PQ = BC,
∵ AN⊥DE,
∴ AM⊥OR,AT⊥BC,
∴ OR = BC = 2BT.
∵ ∠BAC = 120°,
∴ ∠BAM = 60°,
∴ ∠ADN = ∠ABT = 30°. 由(1)知,AB = 30 cm,AD = 10 cm,
∴ AN = $\frac{1}{2}$AD = 5 cm,AT = $\frac{1}{2}$AB = 15 cm,
∴ MN = AM - AN = AB - AN = 25 cm,BT = $\sqrt{AB^{2}-AT^{2}}$ = $15\sqrt{3}$ cm,
∴ OR = 2BT = $30\sqrt{3}$ cm,OP = MN = 25 cm,
∴ 矩形OPQR的长与宽的最小值分别为$30\sqrt{3}$ cm和25 cm.

查看更多完整答案,请扫码查看


