第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.下列说法正确的有 ( )
①各边相等的多边形是正多边形;
②各角相等的多边形是正多边形;
③圆内接菱形是正多边形;
④圆内接矩形是正多边形.
A.1个
B.2个
C.3个
D.0个
①各边相等的多边形是正多边形;
②各角相等的多边形是正多边形;
③圆内接菱形是正多边形;
④圆内接矩形是正多边形.
A.1个
B.2个
C.3个
D.0个
答案:
A 根据正多边形的定义,可知①②④错误,由圆内接菱形的两条对角线互相垂直平分且相等,可知圆内接菱形为正方形,所以③正确。
2.如图所示,△OAB为正三角形,以点O为圆心,OA长为半径作⊙O,直径FC//AB,AO,BO的延长线分别交⊙O于点D,E. 求证:六边形ABCDEF是正六边形.(M9224012)


答案:
证明
∵ △OAB是正三角形,
∴ ∠AOB = ∠OAB = ∠OBA = 60°,
∵ FC//AB,
∴ ∠AOF = ∠OAB = 60°,∠BOC = ∠OBA = 60°,
∴ ∠DOE = ∠AOB = 60°,∠COD = ∠AOF = 60°,∠EOF = ∠BOC = 60°,
∴ ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠AOF,
∴ $\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}=\overset{\frown}{EF}=\overset{\frown}{AF}$,AB = BC = CD = DE = EF = AF,
∴ $\overset{\frown}{BDF}=\overset{\frown}{CDA}=\overset{\frown}{DEB}=\overset{\frown}{EFC}=\overset{\frown}{FAD}=\overset{\frown}{ABE}$,
∴ ∠BAF = ∠ABC = ∠BCD = ∠CDE = ∠DEF = ∠EFA,
∴ 六边形ABCDEF是正六边形。
∵ △OAB是正三角形,
∴ ∠AOB = ∠OAB = ∠OBA = 60°,
∵ FC//AB,
∴ ∠AOF = ∠OAB = 60°,∠BOC = ∠OBA = 60°,
∴ ∠DOE = ∠AOB = 60°,∠COD = ∠AOF = 60°,∠EOF = ∠BOC = 60°,
∴ ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠AOF,
∴ $\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}=\overset{\frown}{EF}=\overset{\frown}{AF}$,AB = BC = CD = DE = EF = AF,
∴ $\overset{\frown}{BDF}=\overset{\frown}{CDA}=\overset{\frown}{DEB}=\overset{\frown}{EFC}=\overset{\frown}{FAD}=\overset{\frown}{ABE}$,
∴ ∠BAF = ∠ABC = ∠BCD = ∠CDE = ∠DEF = ∠EFA,
∴ 六边形ABCDEF是正六边形。
3.教材变式·P49T2在一个半径为2 cm的圆内作出它的内接正六边形及内接正十二边形.(M9224011)
答案:
解析 如图所示,以点O为圆心,2 cm为半径作圆,在⊙O上任找一点A,以点A为圆心,2 cm为半径作弧,交⊙O于点B,然后在⊙O上依次截取等弧(都等于$\overset{\frown}{AB}$),将圆六等分,顺次连接这6个等分点,得到圆的内接正六边形;作线段AB的垂直平分线交⊙O于点C,在⊙O上依次截取相等的弧(都等于$\overset{\frown}{AC}$),顺次连接各等分点得到圆的内接正十二边形。(画法不唯一)
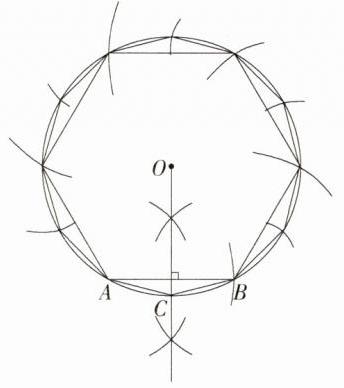
解析 如图所示,以点O为圆心,2 cm为半径作圆,在⊙O上任找一点A,以点A为圆心,2 cm为半径作弧,交⊙O于点B,然后在⊙O上依次截取等弧(都等于$\overset{\frown}{AB}$),将圆六等分,顺次连接这6个等分点,得到圆的内接正六边形;作线段AB的垂直平分线交⊙O于点C,在⊙O上依次截取相等的弧(都等于$\overset{\frown}{AC}$),顺次连接各等分点得到圆的内接正十二边形。(画法不唯一)

4.(2023山西吕梁一模节选,18,★★☆)用尺规作图法作正多边形是数学史上很经典的几何问题,在边数小于10的正多边形中,可以用尺规作图法作出的有正三、正四、正五、正六和正八边形,德国数学家高斯已经证明不能用尺规作图法作出正七边形和正九边形,但是我们可以用下列方法近似地作出一个正七边形:
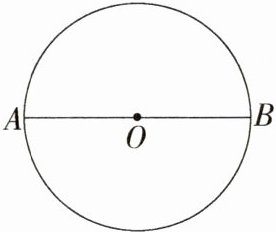
如图,已知AB为⊙O的直径.
步骤一:作出半径OB的垂直平分线,与⊙O交于E,F两点,垂足为D.
步骤二:以ED长为半径,在⊙O上依次截取$\overset{\frown}{BG}=\overset{\frown}{GH}=\overset{\frown}{HM}=\overset{\frown}{MN}=\overset{\frown}{NP}=\overset{\frown}{PQ}=\overset{\frown}{ED}$.
步骤三:顺次连接各分点,即可得到一个近似的正七边形BGHMN PQ.
请根据上面的方法,用直尺(没有刻度)和圆规在已知⊙O中作出正七边形BGHMN PQ.要求:不写作法,但保留作图痕迹.
如图,已知AB为⊙O的直径.
步骤一:作出半径OB的垂直平分线,与⊙O交于E,F两点,垂足为D.
步骤二:以ED长为半径,在⊙O上依次截取$\overset{\frown}{BG}=\overset{\frown}{GH}=\overset{\frown}{HM}=\overset{\frown}{MN}=\overset{\frown}{NP}=\overset{\frown}{PQ}=\overset{\frown}{ED}$.
步骤三:顺次连接各分点,即可得到一个近似的正七边形BGHMN PQ.
请根据上面的方法,用直尺(没有刻度)和圆规在已知⊙O中作出正七边形BGHMN PQ.要求:不写作法,但保留作图痕迹.

答案:
解析 如图所示,七边形BGHMN PQ为所要作的正七边形。
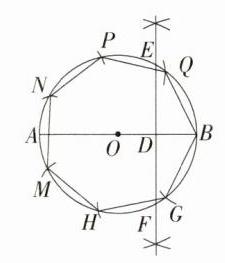
解析 如图所示,七边形BGHMN PQ为所要作的正七边形。

5.(2024江西修水一模,17,★★☆)仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法).
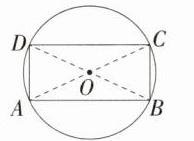
(1)如图1,画出⊙O的一个内接矩形.

(2)如图2,AB是⊙O的直径,CD是弦,且AB//CD,画出⊙O的内接正方形.
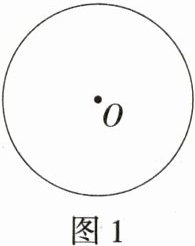

(1)如图1,画出⊙O的一个内接矩形.

(2)如图2,AB是⊙O的直径,CD是弦,且AB//CD,画出⊙O的内接正方形.


答案:
解析 (1)如图所示,过O作⊙O的直径AC与BD,连接AB,BC,CD,DA,则四边形ABCD即为所求。
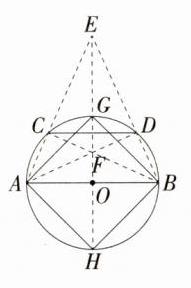
(2)如图所示,连接AC,BD并延长交于点E,连接AD,BC交于点F,连接EF并延长交⊙O于点G,H,连接AH,HB,BG,GA,则四边形AHBG即为所求。
解析 (1)如图所示,过O作⊙O的直径AC与BD,连接AB,BC,CD,DA,则四边形ABCD即为所求。

(2)如图所示,连接AC,BD并延长交于点E,连接AD,BC交于点F,连接EF并延长交⊙O于点G,H,连接AH,HB,BG,GA,则四边形AHBG即为所求。

查看更多完整答案,请扫码查看


