第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024广西宁明一模)下列图案是我国几家银行的标志,其中是中心对称图形的为 ( )
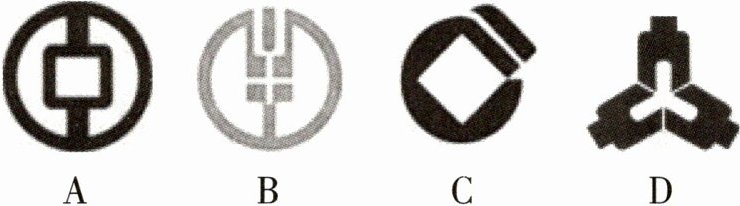
A. B. C. D.

A. B. C. D.
答案:
A:只有 A 选项中的图形绕一点旋转 180°后能与本身重合,是中心对称图形,故选 A。
2. 下列语句描述的是随机事件的为 ( )
A. 垂直于弦的直径平分弦
B. 平分弦的直径垂直于弦
C. 直径所对的圆周角是直角
D. 直径是圆中最长的弦
A. 垂直于弦的直径平分弦
B. 平分弦的直径垂直于弦
C. 直径所对的圆周角是直角
D. 直径是圆中最长的弦
答案:
B:A、C、D 是必然事件,B 中的语句不一定成立,当被平分的弦不是直径时才成立,故 B 是随机事件。
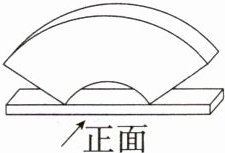
3.(2024安徽阜阳二模)小明制作了一个如图所示的象征美好寓意的摆件,其俯视图是 ( )
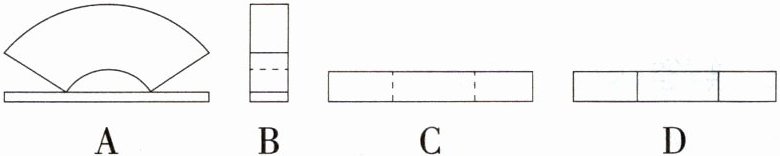


答案:
C:从上面看,该图形俯视图是长方形,且长方形中有两条虚线,即 C 选项的图形符合,故选 C。
4. 新独家原创 如图,AB是⊙O的直径,C、D分别是在AB两侧的圆上的点,则∠C与∠D的关系是 ( )

A. ∠C>∠D
B. ∠C<∠D
C. ∠C=∠D
D. 不能确定

A. ∠C>∠D
B. ∠C<∠D
C. ∠C=∠D
D. 不能确定
答案:
C:
∵ AB 是⊙O 的直径,
∴ ∠C = 90°,∠D = 90°,
∴ ∠C = ∠D,故选 C。
∵ AB 是⊙O 的直径,
∴ ∠C = 90°,∠D = 90°,
∴ ∠C = ∠D,故选 C。
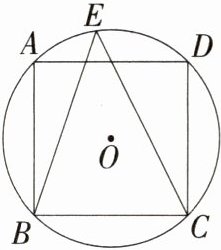
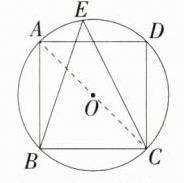
5.(2024安徽合肥模拟)如图,正方形ABCD内接于⊙O,点E在⊙O上,连接BE,CE,若∠ABE = 18°,则∠BEC - ∠DCE = ( )
A. 16°
B. 17°
C. 18°
D. 20°

A. 16°
B. 17°
C. 18°
D. 20°
答案:
C:连接 AC,
∵ 正方形 ABCD 内接于⊙O,点 E 在⊙O 上,∠ABE = 18°,
∴ ∠ACE = ∠ABE = 18°,∠ABC = 90°,∠BAC = ∠ACD = ∠BEC = 45°,
∴ ∠DCE = ∠ACD - ∠ACE = 45° - 18° = 27°,
∴ ∠BEC - ∠DCE = 45° - 27° = 18°,故选 C。
C:连接 AC,
∵ 正方形 ABCD 内接于⊙O,点 E 在⊙O 上,∠ABE = 18°,
∴ ∠ACE = ∠ABE = 18°,∠ABC = 90°,∠BAC = ∠ACD = ∠BEC = 45°,
∴ ∠DCE = ∠ACD - ∠ACE = 45° - 18° = 27°,
∴ ∠BEC - ∠DCE = 45° - 27° = 18°,故选 C。

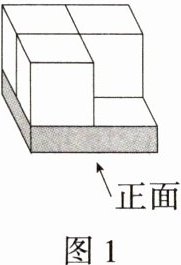
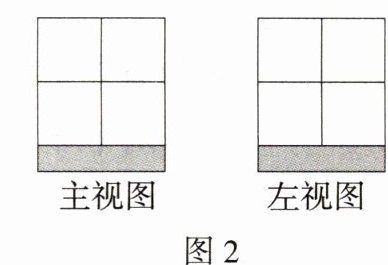
6.(2024安徽合肥模拟)如图1,一个2×2的平台上已经放了三个棱长为1的小正方体,要得到一个几何体,其主视图和左视图如图2所示,平台上至少还需再放这样的小正方体 ( )
A. 1个
B. 2个
C. 3个
D. 4个


A. 1个
B. 2个
C. 3个
D. 4个
答案:
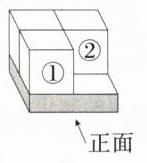
B:如图,只需要在①和②两个小正方体上方各加一个小正方体即可,
∴ 至少还需再放 2 个这样的小正方体,故选 B。
B:如图,只需要在①和②两个小正方体上方各加一个小正方体即可,
∴ 至少还需再放 2 个这样的小正方体,故选 B。

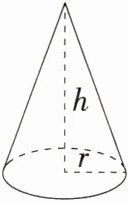
7.(2024广西北流期末)如图,圆锥的高h = 2√2 cm,底面半径r = 1 cm,则该圆锥的侧面积是( )
A. 6π m²
B. 3/2π cm²
C. 3π cm²
D. 2π cm²

A. 6π m²
B. 3/2π cm²
C. 3π cm²
D. 2π cm²
答案:
C:圆锥的母线长是$\sqrt{(2\sqrt{2})^{2}+1^{2}} = 3(cm)$,则圆锥的侧面积是$\pi rl = 3\pi cm^{2}$。故选 C。
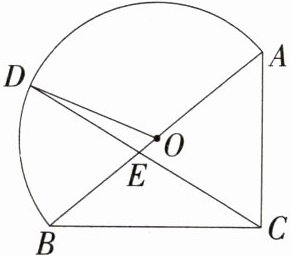
8.(2024湖北广水模拟)如图,在Rt△ABC中,∠ABC = 40°,AB = 6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接OD,CD,CD与AB交于点E,当BE = BC时,弧BD的长为 ( )
A. 4/3π
B. 7/3π
C. 2/3π
D. 7/6π

A. 4/3π
B. 7/3π
C. 2/3π
D. 7/6π
答案:
B:如图,当 BE = BC 时,
∵ ∠ABC = 40°,
∴ ∠BCE = ∠BEC = $\frac{1}{2}\times(180° - 40°) = 70°$,
∴ ∠BOD = 2∠BCE = 140°。
∵ AB = 6,AB 是半圆 O 的直径,
∴ 半圆 O 的半径为 3,
∴ 弧 BD 的长 = $\frac{140\pi\times3}{180}=\frac{7}{3}\pi$。故选 B。
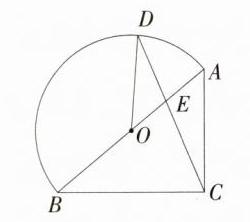
B:如图,当 BE = BC 时,
∵ ∠ABC = 40°,
∴ ∠BCE = ∠BEC = $\frac{1}{2}\times(180° - 40°) = 70°$,
∴ ∠BOD = 2∠BCE = 140°。
∵ AB = 6,AB 是半圆 O 的直径,
∴ 半圆 O 的半径为 3,
∴ 弧 BD 的长 = $\frac{140\pi\times3}{180}=\frac{7}{3}\pi$。故选 B。

查看更多完整答案,请扫码查看


