《2025年5年中考3年模拟九年级数学下册沪科版》

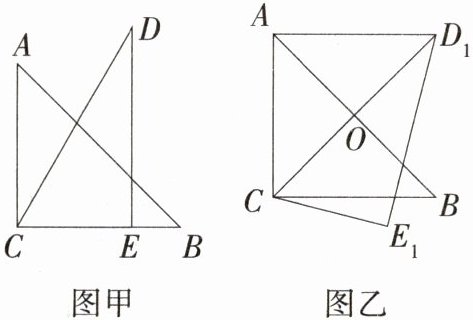
9.(2024黑龙江大庆让胡路模拟改编)两个三角形按如图甲所示方式放置，其中∠ACB = ∠DEC = 90°，∠A = 45°，∠D = 30°，斜边AB = 6，DC = 6，把△DCE绕点C顺时针旋转15°得到△D₁CE₁(如图乙)，此时AB与CD₁交于点O，则线段AD₁的长为 ( )

A. 3√2
B. 5
C. 4
D. √31

答案： A：
∵ ∠ACB = ∠DEC = 90°，∠D = 30°，
∴ ∠DCE = 90° - 30° = 60°，
∴ ∠ACD = 90° - 60° = 30°，
∵ 旋转角为 15°，
∴ ∠ACD₁ = 30° + 15° = 45°， 又
∵ ∠CAB = 45°，
∴ △ACO 是等腰直角三角形，∠AOC = 90°，
∴ AO = CO。
∵ CA = CB，
∴ AO = CO = $\frac{1}{2}AB = \frac{1}{2}\times6 = 3$，
∵ DC = 6，
∴ D₁C = DC = 6，
∴ D₁O = 6 - 3 = 3， 在 Rt△AOD₁ 中，$AD_{1}=\sqrt{AO^{2}+D_{1}O^{2}}=\sqrt{3^{2}+3^{2}} = 3\sqrt{2}$。 故选 A。

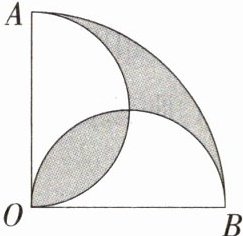
10. 如图，在圆心角为直角的扇形AOB中，分别以OA、OB为直径作两个半圆，在扇形AOB内随机取一点，则该点刚好属于阴影部分的概率是 ( )

A. 1/π
B. 1/2 - 1/π
C. 2/π
D. 1 - 2/π

答案：
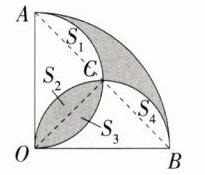
D：如图，设以 OA、OB 为直径所作的两个半圆除公共点 O 外交于点 C，连接 OC，AC，BC，易知$S_{1}=S_{2}=S_{3}=S_{4}$，设扇形 AOB 的半径为 r，则$S_{扇形AOB}=\frac{1}{4}\pi r^{2}$，$S_{\triangle AOB}=\frac{1}{2}r^{2}$，
∴ 图中阴影部分的面积为$\frac{1}{4}\pi r^{2}-\frac{1}{2}r^{2}$，
∴ 在扇形 AOB 内随机取一点，该点刚好属于阴影部分的概率是$\frac{\frac{1}{4}\pi r^{2}-\frac{1}{2}r^{2}}{\frac{1}{4}\pi r^{2}} = 1-\frac{2}{\pi}$。故选 D。

11.(2024甘肃白银期末)广场上，一个大型字母宣传牌垂直于地面放置，其投影如图所示，则该投影属于________.(填“平行投影”或“中心投影”)

答案： 中心投影

12. 新考法·圆与概率综合 已知⊙O的半径为5 cm，点A，B，C，D，E与点O的距离分别为3 cm，5 cm，4 cm，6 cm，6.45 cm，从点O，A，B，C，D，E中任选一个点，这个点在⊙O内的概率为______.

答案： $\frac{1}{2}$ **解析**：本题借助圆的知识考查概率知识。由题意可知六个点中，点 O，A，C 在⊙O 内，所以任选一点在⊙O 内的概率为$\frac{3}{6}=\frac{1}{2}$。

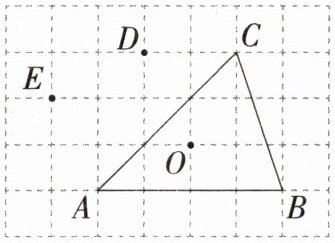
13.(2022广西玉林中考)如图，在5×7网格中，各小正方形边长均为1，点O，A，B，C，D，E均在格点上，点O是△ABC的外心，在不添加其他字母的情况下，把除△ABC外你认为外心也是O的三角形都写出来：____________.

答案： △ADC、△BDC、△ABD **解析**：由题图可知 A、B、C 三点到点 O 的距离均为$\sqrt{1^{2}+2^{2}}=\sqrt{5}$，点 D 到点 O 的距离为$\sqrt{1^{2}+2^{2}}=\sqrt{5}$，点 E 到点 O 的距离为$\sqrt{1^{2}+3^{2}}=\sqrt{10}$，故 A、B、C、D 四点到点 O 的距离相等，故除△ABC 外，外心也是点 O 的三角形有△ADC、△BDC、△ABD。

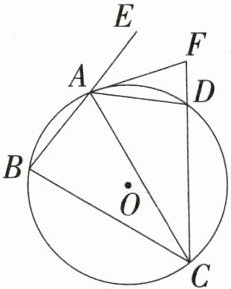
14. 如图，四边形ABCD内接于⊙O，AB = AD，其外角∠EAD的平分线交CD的延长线于点F，CD = 10，AF = 5.
(1)连接AC，若∠BCD = 60°，则∠ACB的度数为_______.
(2)DF的长为_______.

答案： （1）30° （2）$5\sqrt{2}-5$ **解析**：（1）
∵ AB = AD，
∴ ∠ACB = ∠ACD = $\frac{1}{2}\angle BCD$，当∠BCD = 60°时，∠ACB = 30°。 （2）
∵ 四边形 ABCD 内接于⊙O，
∴ ∠BAD + ∠BCD = 180°， 又∠BAD + ∠EAD = 180°，
∴ ∠EAD = ∠BCD，
∵ AF 平分∠EAD，
∴ ∠FAD = $\frac{1}{2}\angle EAD$，
∴ ∠FCA = ∠FAD，又∠AFC = ∠DFA，
∴ △ACF∽△DAF，
∴ $\frac{AF}{DF}=\frac{CF}{AF}$，即$\frac{5}{DF}=\frac{10 + DF}{5}$，
∴ DF = $5\sqrt{2}-5$（已舍负值）。

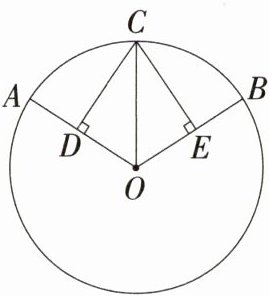
15. [答案含评分细则](2024河南林州期中)(6分)如图，在⊙O中，⌢AC = ⌢BC，CD⊥OA于点D，CE⊥OB于点E. 求证：CD = CE.

答案： 证明：在⊙O 中，$\overset{\frown}{AC}=\overset{\frown}{BC}$，
∴ ∠AOC = ∠BOC，
∴ OC 是∠AOB 的平分线， …… 3 分
∵ CD⊥OA，CE⊥OB，
∴ CD = CE. …… 6 分