第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9.新考法 (2024山东济宁二模)如图,AB为半圆O的直径,现将一块等腰直角三角尺按如图所示方式放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB = 2,则B、Q两点之间的距离为(M9224007) ( )

A.$\sqrt{2}$
B.$\frac{\pi}{2}$
C.$\frac{\pi}{4}$
D.1

A.$\sqrt{2}$
B.$\frac{\pi}{2}$
C.$\frac{\pi}{4}$
D.1
答案:
A:本题借助直角三角尺考查圆周角定理的推论。连接AQ,BQ,因为AB是直径,所以$\angle AQB = 90^{\circ}$。因为$\angle P = 45^{\circ}$,所以$\angle QAB=\angle P = 45^{\circ}$,所以$\triangle ABQ$是等腰直角三角形。因为$AB = 2$,所以$BQ=\sqrt{2}$。故选A。
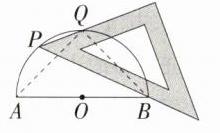
A:本题借助直角三角尺考查圆周角定理的推论。连接AQ,BQ,因为AB是直径,所以$\angle AQB = 90^{\circ}$。因为$\angle P = 45^{\circ}$,所以$\angle QAB=\angle P = 45^{\circ}$,所以$\triangle ABQ$是等腰直角三角形。因为$AB = 2$,所以$BQ=\sqrt{2}$。故选A。

10.一题多解 如图,AB是⊙O的直径,点C是$\overset{\frown}{AB}$的中点,连接AC,BC,D为⊙O上一点,则tan D = _______.


答案:
答案:1 解析:【解法一】因为AB是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。又点C是$\widehat{AB}$的中点,所以$\widehat{BC}=\widehat{AC}$,所以$\angle A=\angle ABC = 45^{\circ}$,所以$\angle D=\angle A = 45^{\circ}$,所以$\tan D=\tan45^{\circ}=1$。 【解法二】如图,连接OC,因为点C是$\widehat{AB}$的中点,所以$\widehat{AC}=\widehat{BC}$。又AB是直径,所以$\angle BOC=\angle AOC = 90^{\circ}$,所以$\angle D=\frac{1}{2}\angle BOC = 45^{\circ}$,所以$\tan D=\tan45^{\circ}=1$。
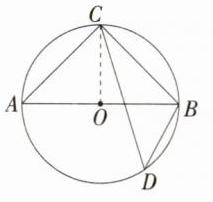
答案:1 解析:【解法一】因为AB是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。又点C是$\widehat{AB}$的中点,所以$\widehat{BC}=\widehat{AC}$,所以$\angle A=\angle ABC = 45^{\circ}$,所以$\angle D=\angle A = 45^{\circ}$,所以$\tan D=\tan45^{\circ}=1$。 【解法二】如图,连接OC,因为点C是$\widehat{AB}$的中点,所以$\widehat{AC}=\widehat{BC}$。又AB是直径,所以$\angle BOC=\angle AOC = 90^{\circ}$,所以$\angle D=\frac{1}{2}\angle BOC = 45^{\circ}$,所以$\tan D=\tan45^{\circ}=1$。

11.构造同弧所对的圆周角 (2022山东淄博张店一模)如图,一块直角三角尺的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,若⊙O的半径为2,则弦AB的长为_______.


答案:
答案:2 解析:如图,连接AO并延长,交$\odot O$于点D,连接BD,因为$\angle P = 30^{\circ}$,所以$\angle D=\angle P = 30^{\circ}$,因为AD是$\odot O$的直径,所以$\angle ABD = 90^{\circ}$,所以$AB=\frac{1}{2}AD = OD = 2$。
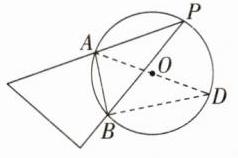
答案:2 解析:如图,连接AO并延长,交$\odot O$于点D,连接BD,因为$\angle P = 30^{\circ}$,所以$\angle D=\angle P = 30^{\circ}$,因为AD是$\odot O$的直径,所以$\angle ABD = 90^{\circ}$,所以$AB=\frac{1}{2}AD = OD = 2$。

12.(2024重庆中考B卷,8,★☆☆)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,连接BD,CD.若∠D = 28°,则∠OAB的度数为(M9224007) ( )
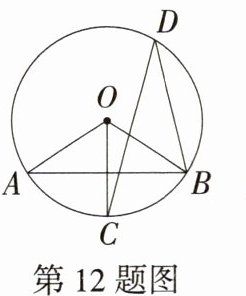
A.28°
B.34°
C.56°
D.62°

A.28°
B.34°
C.56°
D.62°
答案:
B:因为$\angle D = 28^{\circ}$,所以$\angle BOC = 2\angle D = 56^{\circ}$。因为$OC\perp AB$,所以点C为$\widehat{AB}$的中点,$\widehat{AC}=\widehat{BC}$,所以$\angle AOC=\angle BOC = 56^{\circ}$,所以$\angle AOB = 2\times56^{\circ}=112^{\circ}$。因为$OA = OB$,所以$\angle OAB=\frac{1}{2}\times(180^{\circ}-112^{\circ}) = 34^{\circ}$。故选B。
13.(2023吉林中考,6,★☆☆)如图,AB,AC是⊙O的弦,OB,OC是⊙O的半径,点P为OB上任意一点(点P不与点B重合),连接CP.若∠BAC = 70°,则∠BPC的度数可能是 ( )

A.70°
B.105°
C.125°
D.155°

A.70°
B.105°
C.125°
D.155°
答案:
D:如图,连接BC,因为$\angle BAC = 70^{\circ}$,所以$\angle BOC = 2\angle BAC = 140^{\circ}$。因为$OB = OC$,所以$\angle OBC=\angle OCB=\frac{180^{\circ}-140^{\circ}}{2}=20^{\circ}$,因为点P为OB上任意一点(点P不与点B重合),所以$0^{\circ}\leq\angle OCP\lt20^{\circ}$。因为$\angle BPC=\angle BOC+\angle OCP = 140^{\circ}+\angle OCP$,所以$140^{\circ}\leq\angle BPC\lt160^{\circ}$。故选D。
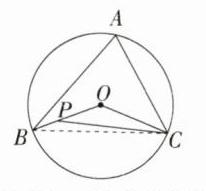
D:如图,连接BC,因为$\angle BAC = 70^{\circ}$,所以$\angle BOC = 2\angle BAC = 140^{\circ}$。因为$OB = OC$,所以$\angle OBC=\angle OCB=\frac{180^{\circ}-140^{\circ}}{2}=20^{\circ}$,因为点P为OB上任意一点(点P不与点B重合),所以$0^{\circ}\leq\angle OCP\lt20^{\circ}$。因为$\angle BPC=\angle BOC+\angle OCP = 140^{\circ}+\angle OCP$,所以$140^{\circ}\leq\angle BPC\lt160^{\circ}$。故选D。

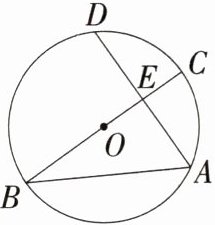
14.(2024安徽霍山三模,7,★★☆)如图,已知⊙O的半径为2,AB,AD是⊙O的弦,BC是⊙O的直径,∠ABC = 30°,弦AD与BC交于点E,且点E是AD的中点,则DE² - CE² = ( )
A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
B:如图,连接DB、DO。因为BC是$\odot O$的直径,点E是AD的中点,所以$BC\perp AD$,$\widehat{CD}=\widehat{CA}$,所以$\angle DBC=\angle ABC = 30^{\circ}$,所以$\angle DOC = 2\angle DBC = 60^{\circ}$,所以$\angle ODE = 30^{\circ}$,所以$OE=\frac{1}{2}OD = 1$,所以$CE = OC - OE = 1$,$DE=\sqrt{OD^{2}-OE^{2}}=\sqrt{3}$,所以$DE^{2}-CE^{2}=3 - 1 = 2$。故选B。
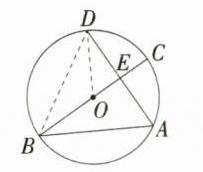
B:如图,连接DB、DO。因为BC是$\odot O$的直径,点E是AD的中点,所以$BC\perp AD$,$\widehat{CD}=\widehat{CA}$,所以$\angle DBC=\angle ABC = 30^{\circ}$,所以$\angle DOC = 2\angle DBC = 60^{\circ}$,所以$\angle ODE = 30^{\circ}$,所以$OE=\frac{1}{2}OD = 1$,所以$CE = OC - OE = 1$,$DE=\sqrt{OD^{2}-OE^{2}}=\sqrt{3}$,所以$DE^{2}-CE^{2}=3 - 1 = 2$。故选B。

15.(2021安徽中考,13,★★☆)如图,圆O的半径为1,△ABC内接于圆O.若∠A = 60°,∠B = 75°,则AB = _______.


答案:
答案:$\sqrt{2}$ 解析:如图,连接OA,OB,在$\triangle ABC$中,$\angle BAC = 60^{\circ}$,$\angle ABC = 75^{\circ}$,所以$\angle ACB = 180^{\circ}-\angle BAC-\angle ABC = 45^{\circ}$,所以$\angle AOB = 90^{\circ}$,因为$OA = OB$,所以$\triangle OAB$是等腰直角三角形,因为圆O的半径为1,即$OA = OB = 1$,所以$AB=\sqrt{2}$。

答案:$\sqrt{2}$ 解析:如图,连接OA,OB,在$\triangle ABC$中,$\angle BAC = 60^{\circ}$,$\angle ABC = 75^{\circ}$,所以$\angle ACB = 180^{\circ}-\angle BAC-\angle ABC = 45^{\circ}$,所以$\angle AOB = 90^{\circ}$,因为$OA = OB$,所以$\triangle OAB$是等腰直角三角形,因为圆O的半径为1,即$OA = OB = 1$,所以$AB=\sqrt{2}$。

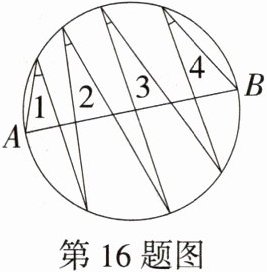
16.(2024江苏连云港中考,14,★★☆)如图,AB是圆的直径,∠1,∠2,∠3,∠4的顶点均在AB上方的圆弧上,∠1,∠4的一边分别经过点A,B,则∠1 + ∠2 + ∠3 + ∠4 = _______°.

答案:
答案:90
解析:由题图可知,$\angle1$,$\angle2$,$\angle3$,$\angle4$这几个圆周角所对的弧之和为半圆AB,半圆AB所对的圆心角为$180^{\circ}$,则$\angle1+\angle2+\angle3+\angle4 = 90^{\circ}$。
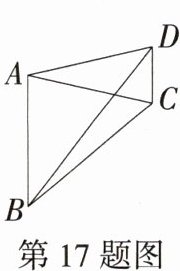
17.构造辅助圆 教材变式·P29T3 (2024山东巨野期中,12,★★☆)如图,在四边形ABCD中,AB = AC = AD,∠DBC = $\frac{1}{3}$∠BDC.如果∠DAC = 25°,那么∠BAC = _______°. (M9224007)

答案:
答案:75 解析:因为$AB = AC = AD$,所以点B、C、D在以点A为圆心,AB长为半径的同一个圆上(如图)。 因为$\angle DAC = 25^{\circ}$,所以$\angle DBC=\frac{1}{2}\angle DAC = 12.5^{\circ}$。 因为$\angle DBC=\frac{1}{3}\angle BDC$, 所以$\angle BDC = 3\angle DBC = 37.5^{\circ}$,所以$\angle BAC = 2\angle BDC = 75^{\circ}$。
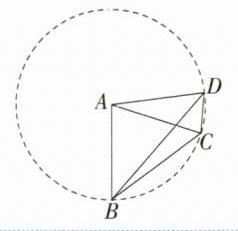
答案:75 解析:因为$AB = AC = AD$,所以点B、C、D在以点A为圆心,AB长为半径的同一个圆上(如图)。 因为$\angle DAC = 25^{\circ}$,所以$\angle DBC=\frac{1}{2}\angle DAC = 12.5^{\circ}$。 因为$\angle DBC=\frac{1}{3}\angle BDC$, 所以$\angle BDC = 3\angle DBC = 37.5^{\circ}$,所以$\angle BAC = 2\angle BDC = 75^{\circ}$。

查看更多完整答案,请扫码查看


