《2025年5年中考3年模拟九年级数学下册沪科版》

1.将一个直角三角形绕其一条直角边所在直线旋转一周，所得几何体的正投影可能是（ ）
A.正方形
B.等腰三角形
C.线段
D.点

答案： B：将一个直角三角形绕其一条直角边所在直线旋转一周，所得的几何体是圆锥，圆锥的正投影可能是等腰三角形，故选B。

2.(2024江西万载月考)一根长为m的木棒在一投影面上形成的正投影的长为3，则m的取值范围为________.

答案： 答案：$m\geq3$ 解析：由线段的正投影规律“平行长不变，倾斜长缩短，垂直成一点”可知线段的长$\geq$该线段正投影的长。木棒可看成线段，所以$m\geq3$。

3.如图，下列投影中，正投影是________（只填序号）.

答案： 答案：③④ 解析：①不是平行投影；②中的投射线不垂直于投影面，不是正投影；③④的投影是正投影。

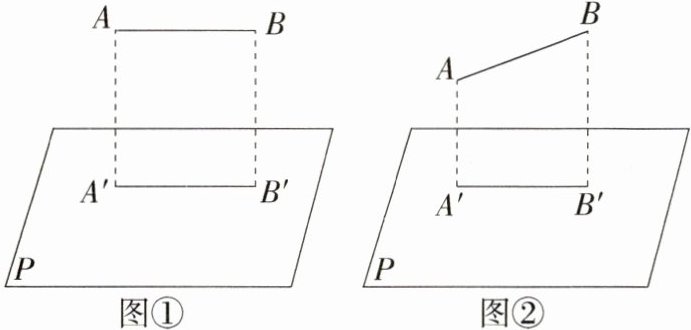
4.如图，已知线段AB的长为1，投影面为P.
(1)如图①，当AB平行于投影面P时，它的正投影A'B'的长是多少?
(2)在(1)的基础上，点B不动，线段AB绕着点B在垂直于P的平面内逆时针旋转30°，如图②，这时AB的正投影A'B'的长度比原来的变小了，试求出这时A'B'比(1)中的A'B'短了多少.

答案：
解析：
(1)$A'B' = AB = 1$。
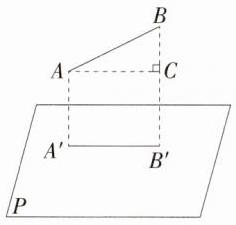
(2)如图，过$A$作$AC\perp BB'$于点$C$， 则$A'B' = AC = AB\cdot\cos30^{\circ}=\frac{\sqrt{3}}{2}$。 $\because1 - \frac{\sqrt{3}}{2}=\frac{2 - \sqrt{3}}{2}$， $\therefore$这时$A'B'$比
(1)中的$A'B'$短$\frac{2 - \sqrt{3}}{2}$。

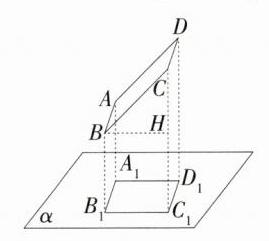
5.如图，正方形纸板ABCD在投影面α上的正投影为A₁B₁C₁D₁，其中边AB、CD与投影面平行，AD，BC与投影面不平行.若正方形ABCD的边长为5 cm，∠BCC₁ = 45°，求其投影A₁B₁C₁D₁的面积.(M9225001)

答案：
解析：过$B$点作$BH\perp CC_1$于$H$，如图， $\because\angle BCC_1 = 45^{\circ}$，$\therefore\triangle BCH$是等腰直角三角形， $\therefore BH=\frac{\sqrt{2}}{2}BC=\frac{5\sqrt{2}}{2}\text{cm}$， $\because$正方形纸板$ABCD$在投影面$\alpha$上的正投影为$A_1B_1C_1D_1$，$\therefore B_1C_1 = BH=\frac{5\sqrt{2}}{2}\text{cm}$，$C_1D_1 = CD = 5\text{cm}$， $\therefore$投影$A_1B_1C_1D_1$的面积$=\frac{5\sqrt{2}}{2}\times5=\frac{25\sqrt{2}}{2}(\text{cm}^2)$。

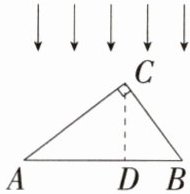
6.如图，在Rt△ABC中，∠ACB = 90°，投影线方向如图所示，点C在斜边AB上的正投影为点D.(M9225001)
(1)试写出边AC、BC在AB上的投影.
(2)试探究线段AC、AB和AD之间的数量关系.
(3)线段BC、AB和BD之间也有类似的关系，请直接写出结论.

答案： 解析：
(1)边$AC$、$BC$在$AB$上的投影分别为$AD$、$BD$。
(2)$\because$点$C$在斜边$AB$上的正投影为点$D$， $\therefore CD\perp AB$，$\therefore\angle ADC = 90^{\circ}=\angle ACB$。 又$\because\angle DAC=\angle CAB$，$\therefore\triangle ADC\sim\triangle ACB$， $\therefore AC:AB = AD:AC$，$\therefore AC^2 = AD\cdot AB$。
(3)$BC^2 = BD\cdot AB$。