第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
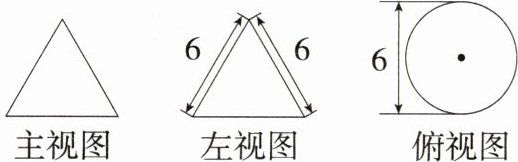
17.(2024陕西蓝田月考)(6分)如图所示的是一个几何体的三视图.
(1)写出几何体的名称.
(2)根据图中标出的数据,计算这个几何体的表面积(精确到0.1 cm²,即结果保留一位小数).
(1)写出几何体的名称.
(2)根据图中标出的数据,计算这个几何体的表面积(精确到0.1 cm²,即结果保留一位小数).

答案:
解析 (1)由三视图可知,该几何体是圆锥。
(2)这个几何体的表面积:$\frac{1}{2}\cdot2\pi r\cdot l+\pi r^{2}=\frac{1}{2}\times2\pi\times3\times6+\pi\times3^{2}=27\pi\approx84.8$ cm²。
18.(2024江苏苏州期末)(6分)如图所示的是由大小相同的小立方块搭成的几何体,按要求解答下列问题:
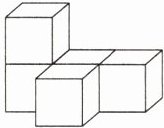
(1)在网格图中画出该几何体的主视图和左视图.
(2)若现在你手头还有一些相同的小立方块,保持主视图和左视图不变,则在图中最多可以再添加________个小立方块.

(1)在网格图中画出该几何体的主视图和左视图.
(2)若现在你手头还有一些相同的小立方块,保持主视图和左视图不变,则在图中最多可以再添加________个小立方块.

答案:
解析 (1)如图所示。
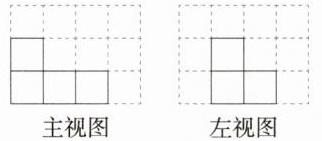
(2)如图所示,最多可以再添加2个小立方块。
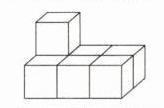
解析 (1)如图所示。

(2)如图所示,最多可以再添加2个小立方块。

19.(6分)如图,在一地面的正上方有一路灯P,小明想测量路灯P到地面的距离,于是他将一根长度为1 m的标杆AB按如图所示的方式放置,使AB与地面平行,得到标杆AB在地面上的影子CD.(M9225001)
(1)请在图中画出路灯P的位置.
(2)若测得标杆AB与地面之间的距离是1 m,此时AB在地面上的影子CD = 1.4 m,求路灯P到地面的距离.
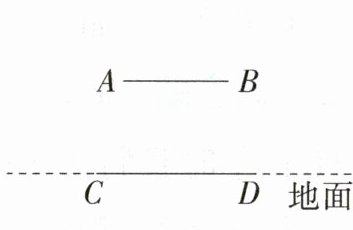
(1)请在图中画出路灯P的位置.
(2)若测得标杆AB与地面之间的距离是1 m,此时AB在地面上的影子CD = 1.4 m,求路灯P到地面的距离.
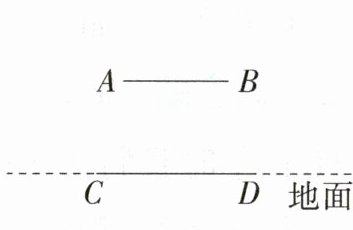
答案:
解析 (1)路灯P的位置如图所示。

(2)如图,过P点作PE⊥CD于E,交AB于点F。
∵AB//CD,
∴△PAB∽△PCD,
∴$\frac{AB}{CD}=\frac{PF}{PE}$。
∵AB = 1,EF = 1,CD = 1.4,
∴$\frac{1}{1.4}=\frac{PE - 1}{PE}$,
∴PE = 3.5 m。
∴路灯P到地面的距离为3.5 m。
解析 (1)路灯P的位置如图所示。

(2)如图,过P点作PE⊥CD于E,交AB于点F。
∵AB//CD,
∴△PAB∽△PCD,
∴$\frac{AB}{CD}=\frac{PF}{PE}$。
∵AB = 1,EF = 1,CD = 1.4,
∴$\frac{1}{1.4}=\frac{PE - 1}{PE}$,
∴PE = 3.5 m。
∴路灯P到地面的距离为3.5 m。
20.(2024广东深圳宝安中学期中)(6分)甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地10时,物高与影长的比是1∶$\sqrt{2}$.
(1)如图1,当地10时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为________米.
(2)当地8时,物高与影长的比是1∶2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
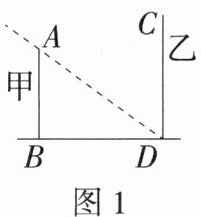
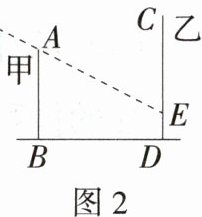
(1)如图1,当地10时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为________米.
(2)当地8时,物高与影长的比是1∶2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.


答案:
解析 (1)由题意得$\frac{AB}{BD}=\frac{1}{\sqrt{2}}$,即$\frac{16}{BD}=\frac{1}{\sqrt{2}}$, 解得$BD = 16\sqrt{2}$米,故答案为$16\sqrt{2}$。 (2)如图,作EF⊥AB于点F, 在Rt△AEF中,∠AFE = 90°,EF = BD = $16\sqrt{2}$米,
∵物高与影长的比是1∶2,
∴$\frac{AF}{EF}=\frac{1}{2}$,
∴$AF=\frac{1}{2}EF=\frac{1}{2}\times16\sqrt{2}=8\sqrt{2}$(米),
∴DE = BF = AB - AF = $(16 - 8\sqrt{2})$米, 即落在乙楼上的影子DE的长为$(16 - 8\sqrt{2})$米。

解析 (1)由题意得$\frac{AB}{BD}=\frac{1}{\sqrt{2}}$,即$\frac{16}{BD}=\frac{1}{\sqrt{2}}$, 解得$BD = 16\sqrt{2}$米,故答案为$16\sqrt{2}$。 (2)如图,作EF⊥AB于点F, 在Rt△AEF中,∠AFE = 90°,EF = BD = $16\sqrt{2}$米,
∵物高与影长的比是1∶2,
∴$\frac{AF}{EF}=\frac{1}{2}$,
∴$AF=\frac{1}{2}EF=\frac{1}{2}\times16\sqrt{2}=8\sqrt{2}$(米),
∴DE = BF = AB - AF = $(16 - 8\sqrt{2})$米, 即落在乙楼上的影子DE的长为$(16 - 8\sqrt{2})$米。

查看更多完整答案,请扫码查看


