《2025年5年中考3年模拟九年级数学下册沪科版》

8.如图,AB是⊙O的直径,CD是⊙O的弦,且CE=DE,∠COB = 52°,则∠DCO的度数为(M9224006) （ ）

A.52°
B.50°
C.48°
D.38°

答案： D：因为AB是直径，CE = ED，所以AB⊥CD，所以∠CEO = 90°，所以∠DCO = 90° - 52° = 38°，故选D。

9.(2024湖南长沙一模改编)如图,⊙O的半径OC交弦AB于点D,AD=DB,OD=6,CD=4,则AB的长为(M9224006) （ ）

A.6
B.8
C.16
D.18

答案： C：连接OA（图略），因为AD = DB，所以CO⊥AB；因为OD = 6，CD = 4，所以OA = CO = 6 + 4 = 10，所以$AD=\sqrt{OA^{2}-OD^{2}} = 8$，所以AB = 2AD = 16，故选C。

10.(2024安徽六安皋城中学月考)如图,⊙O的直径AB=10 cm,C是⊙O上一点,点D平分$\overset{\frown}{BC}$,OD交BC于点E,且DE = 1 cm,则弦AC =________cm.

答案： 答案：8 解析：因为点D平分$\overset{\frown}{BC}$，所以OD平分BC，所以OE为△ABC的中位线；因为⊙O的直径AB = 10 cm，所以OD = 5 cm；因为DE = 1 cm，所以OE = 4 cm，则弦AC = 2OE = 8 cm。

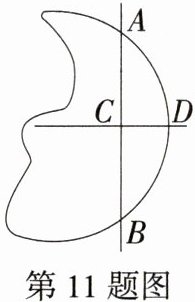
11.(2024陕西西安模拟)如图,古人在计算残缺的、不确定圆心的圆形物件的半径时,会采用以下方法:在圆上找两点A,B,连接AB,确定AB的中点C,$\overset{\frown}{AB}$的中点D,并作过点C,D的直线.若测得AB为20分米,CD为5分米,则该圆的半径为________分米.(M9224006)

答案： 答案：$\frac{25}{2}$ 解析：设圆心为O，因为C为AB的中点，D为$\overset{\frown}{AB}$的中点，AB = 20分米，所以AC = CB = 10分米，$\overset{\frown}{AD}=\overset{\frown}{DB}$，所以直线CD经过圆心O，OD⊥AB，连接AO（图略）。设OA = OD = r分米，则OC = (r - 5)分米，在Rt△AOC中，由勾股定理得$OA^{2}=AC^{2}+OC^{2}$，即$r^{2}=10^{2}+(r - 5)^{2}$，解得$r=\frac{25}{2}$，即该圆的半径为$\frac{25}{2}$分米。

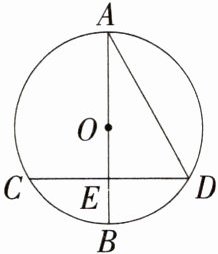
12.(2024上海青浦二模)如图,A、B、C、D均在⊙O上,AB是⊙O的直径,AB与CD相交于点E,AD =CD,$\overset{\frown}{BC}=\overset{\frown}{BD}$.
(1)求∠ADC的度数.
(2)如果OE=1,求AD的长.

答案：
解析\n
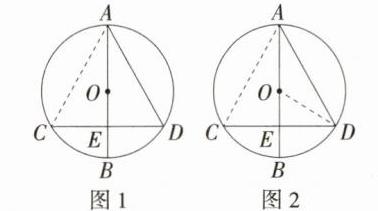
(1)连接AC，如图1。因为AB是⊙O的直径，$\overset{\frown}{BC}=\overset{\frown}{BD}$，所以AB⊥CD，$CE = DE=\frac{1}{2}CD$，所以AC = AD = CD，所以△ACD是等边三角形，所以∠ADC = 60°。\n
(2)连接OD，如图2。由
(1)知$DE = EC=\frac{1}{2}CD$，AB⊥CD，所以∠AED = 90°；因为∠ADC = 60°，所以∠DAO = 90° - ∠ADC = 30°；因为OA = OD，所以∠ODA = ∠DAO = 30°，所以∠DOE = 60°。在Rt△OED中，OE = 1，所以$DE = OE\cdot\tan60^{\circ}=\sqrt{3}$，所以$CD = 2DE = 2\sqrt{3}$，所以AD = CD = $2\sqrt{3}$。

13.寿春路桥(图①)横跨合肥市母亲河——南淝河,它位于合肥市东西交通主干道寿春路上,建成于1987年年底,为中承式钢筋砼拱桥,桥的上部结构为两个钢筋混凝土半月形拱肋,图②是桥拱肋的简化示意图,其中拱宽(弦AB)约为100米.
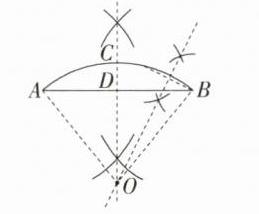
(1)在图②中,请你用尺规作图的方法首先找出弧AB所在圆的圆心O,然后分别确定弧AB、弦AB的中点C、D.(不要求写作法,保留作图痕迹)
(2)在完成(1)中作图后的图②中,若∠AOB=80°,求该桥拱肋的高CD约为多少米.(结果精确到0.1米,参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)

答案：
解析\n
(1)如图所示。\n
(2)如图，连接OA，OB，易知OC垂直平分AB，且OC平分∠AOB，所以$AD=\frac{1}{2}AB = 50$米，∠AOD = 40°，所以∠DAO = 50°，所以$OD = AD\cdot\tan50^{\circ}\approx50\times1.19 = 59.5$（米），$OA=\frac{AD}{\cos50^{\circ}}\approx\frac{50}{0.64}\approx78.13$（米），所以$CD = OC - OD = OA - OD\approx18.6$（米）。