第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
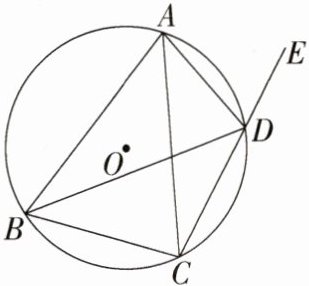
8.构造直径 (2022山东威海中考,20,★★☆)如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.
(1)若AB = AC,求证:∠ADB = ∠ADE.
(2)若BC = 3,⊙O的半径为2,求sin∠BAC.
(1)若AB = AC,求证:∠ADB = ∠ADE.
(2)若BC = 3,⊙O的半径为2,求sin∠BAC.

答案:
解析
(1) **证明**:因为四边形ABCD是⊙O的内接四边形,所以∠ADE = ∠ABC。因为AB = AC,所以∠ABC = ∠ACB。因为∠ACB = ∠ADB,所以∠ADB = ∠ADE。
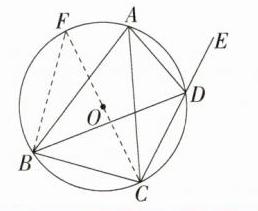
(2) 如图,连接CO并延长交⊙O于点F,连接BF,则∠FBC = 90°。在Rt△BCF中,CF = 4,BC = 3,所以sin F = $\frac{BC}{CF}=\frac{3}{4}$,因为∠F = ∠BAC,所以sin∠BAC = $\frac{3}{4}$。
解析
(1) **证明**:因为四边形ABCD是⊙O的内接四边形,所以∠ADE = ∠ABC。因为AB = AC,所以∠ABC = ∠ACB。因为∠ACB = ∠ADB,所以∠ADB = ∠ADE。
(2) 如图,连接CO并延长交⊙O于点F,连接BF,则∠FBC = 90°。在Rt△BCF中,CF = 4,BC = 3,所以sin F = $\frac{BC}{CF}=\frac{3}{4}$,因为∠F = ∠BAC,所以sin∠BAC = $\frac{3}{4}$。

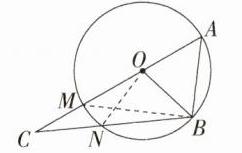
9.创新意识 (2024河北邢台威县期末)如图,已知△ABC,O为AC上一点,以O为圆心,OB长为半径的圆经过点A,且与BC、OC交于点N、M,设∠C = α,∠A = β,则 ( )

A.若α - β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为15°
B.若α - β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为30°
C.若α + β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为15°
D.若α + β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为30°

A.若α - β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为15°
B.若α - β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为30°
C.若α + β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为15°
D.若α + β = 75°,则$\overset{\frown}{MN}$所对应的圆心角为30°
答案:
D 如图,连接ON、BM,所以∠MON = 2∠MBN。因为AM是⊙O的直径,所以∠ABM = 90°,因为∠A = β,所以∠AMB = 90° - β,因为∠AMB = ∠C + ∠CBM,∠C = α,所以∠MBN = 90° - β - α,所以∠MON = 180° - 2(α + β)。当α - β = 75°时,∠MON = 30° - 4β,故A、B选项不符合题意;当α + β = 75°时,∠MON = 180° - 75°×2 = 30°,故C选项不符合题意,D选项符合题意,故选D。
D 如图,连接ON、BM,所以∠MON = 2∠MBN。因为AM是⊙O的直径,所以∠ABM = 90°,因为∠A = β,所以∠AMB = 90° - β,因为∠AMB = ∠C + ∠CBM,∠C = α,所以∠MBN = 90° - β - α,所以∠MON = 180° - 2(α + β)。当α - β = 75°时,∠MON = 30° - 4β,故A、B选项不符合题意;当α + β = 75°时,∠MON = 180° - 75°×2 = 30°,故C选项不符合题意,D选项符合题意,故选D。

10.推理能力 (2023江苏扬州邗江期中)某版本教材在探究圆内接四边形中对角的数量关系时提出了两个问题:
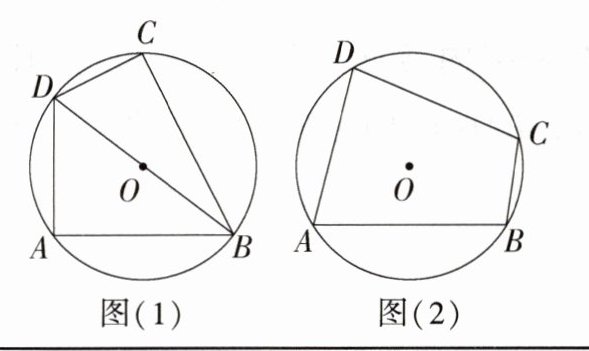
1.如图(1),四边形ABCD是⊙O的内接四边形,BD是⊙O的直径,∠A与∠C、∠ABC与∠ADC有怎样的数量关系?
2.如图(2),若圆心O不在⊙O的内接四边形ABCD的对角线上,问题1中发现的结论是否仍然成立?
(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系,请帮助他完善问题1的证明:
∵BD是⊙O的直径,
∴______________,
∴∠A + ∠C = 180°,
∵四边形内角和等于360°,
∴______________.
(2)请回答问题2,并说明理由.
(3)如图,点A、B、C、D、E、F在⊙O上,AD//EF,CE//AB,请用上面发现的结论证明CD//BF.
1.如图(1),四边形ABCD是⊙O的内接四边形,BD是⊙O的直径,∠A与∠C、∠ABC与∠ADC有怎样的数量关系?
2.如图(2),若圆心O不在⊙O的内接四边形ABCD的对角线上,问题1中发现的结论是否仍然成立?

(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系,请帮助他完善问题1的证明:
∵BD是⊙O的直径,
∴______________,
∴∠A + ∠C = 180°,
∵四边形内角和等于360°,
∴______________.
(2)请回答问题2,并说明理由.
(3)如图,点A、B、C、D、E、F在⊙O上,AD//EF,CE//AB,请用上面发现的结论证明CD//BF.
答案:
解析
(1) ∠A = ∠C = 90°;∠ABC + ∠ADC = 180°。
(2) 结论仍然成立。理由:因为∠A所对的弧为$\overset{\frown}{DCB}$,∠C所对的弧为$\overset{\frown}{DAB}$,所以∠A所对的弧$\overset{\frown}{DCB}$+∠C所对的弧$\overset{\frown}{DAB}$为整个圆周,所以∠A + ∠C = $\frac{1}{2}\times360° = 180°$。因为四边形内角和等于360°,所以∠ABC + ∠ADC = 180°。
(3) **证明**:如图,因为四边形ABCD为圆内接四边形,所以∠A + ∠DCB = 180°。因为AD//EF,所以∠A = ∠1,所以∠1 + ∠DCB = 180°。因为AB//EC,所以∠1 + ∠E = 180°,所以∠E = ∠DCB。因为四边形BCEF为圆内接四边形,所以∠E + ∠FBC = 180°,所以∠DCB + ∠FBC = 180°,所以CD//FB。

解析
(1) ∠A = ∠C = 90°;∠ABC + ∠ADC = 180°。
(2) 结论仍然成立。理由:因为∠A所对的弧为$\overset{\frown}{DCB}$,∠C所对的弧为$\overset{\frown}{DAB}$,所以∠A所对的弧$\overset{\frown}{DCB}$+∠C所对的弧$\overset{\frown}{DAB}$为整个圆周,所以∠A + ∠C = $\frac{1}{2}\times360° = 180°$。因为四边形内角和等于360°,所以∠ABC + ∠ADC = 180°。
(3) **证明**:如图,因为四边形ABCD为圆内接四边形,所以∠A + ∠DCB = 180°。因为AD//EF,所以∠A = ∠1,所以∠1 + ∠DCB = 180°。因为AB//EC,所以∠1 + ∠E = 180°,所以∠E = ∠DCB。因为四边形BCEF为圆内接四边形,所以∠E + ∠FBC = 180°,所以∠DCB + ∠FBC = 180°,所以CD//FB。

查看更多完整答案,请扫码查看


