第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
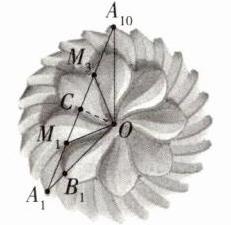
15.推理能力 杭州奥体中心网球中心以“莲花”造型惊艳众人,又名“小莲花”.该建筑底部是由24片全等“花瓣”组成的“固定花环”,上方穹顶由8片全等“旋转花瓣”均匀连接,可根据天气变化合拢或旋转展开.小明借助圆的内接正多边形的知识,模拟“小莲花”变化状态.如图,穹顶合拢时,正二十四边形顶点A₁,正八边形顶点B₁与圆心O共线,正二十四边形顶点A₁,A₁₀与正八边形顶点M₁,M₃共线,连接OA₁₀,OM₁,OM₃,则$\frac{A_{1}A_{10}}{M_{1}M_{3}}$的值为_______.


答案:
答案:$1+\sqrt{2}$ 解析:如图,过O作$OC\perp A_{1}A_{10}$,由题意知$\angle M_{1}OM_{3}=\frac{360^{\circ}}{8}\times2 = 90^{\circ}$,$\angle A_{1}OA_{10}=\frac{360^{\circ}}{24}\times9 = 135^{\circ}$,因为$OA_{10}=OA_{1}$,$OM_{3}=OM_{1}$,所以$\angle COM_{3}=\frac{90^{\circ}}{2}=45^{\circ}$,$\angle COA_{10}=\frac{135^{\circ}}{2}=67.5^{\circ}$,所以$\angle COM_{3}=\angle OM_{3}C = 45^{\circ}$,所以$CM_{3}=OC$,$OM_{3}=\sqrt{2}OC$,所以$M_{1}M_{3}=2OC$,因为$\angle A_{10}OM_{3}=67.5^{\circ}-45^{\circ}=22.5^{\circ}$,$\angle M_{3}A_{10}O = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,所以$\angle A_{10}OM_{3}=\angle M_{3}A_{10}O$,所以$A_{10}M_{3}=OM_{3}=\sqrt{2}OC$,所以$A_{10}C = OC+\sqrt{2}OC$,所以$A_{1}A_{10}=2A_{10}C = 2OC+2\sqrt{2}OC=(1+\sqrt{2})\cdot2OC$,所以$\frac{A_{1}A_{10}}{M_{1}M_{3}}=\frac{(1+\sqrt{2})\cdot2OC}{2OC}=1+\sqrt{2}$。
答案:$1+\sqrt{2}$ 解析:如图,过O作$OC\perp A_{1}A_{10}$,由题意知$\angle M_{1}OM_{3}=\frac{360^{\circ}}{8}\times2 = 90^{\circ}$,$\angle A_{1}OA_{10}=\frac{360^{\circ}}{24}\times9 = 135^{\circ}$,因为$OA_{10}=OA_{1}$,$OM_{3}=OM_{1}$,所以$\angle COM_{3}=\frac{90^{\circ}}{2}=45^{\circ}$,$\angle COA_{10}=\frac{135^{\circ}}{2}=67.5^{\circ}$,所以$\angle COM_{3}=\angle OM_{3}C = 45^{\circ}$,所以$CM_{3}=OC$,$OM_{3}=\sqrt{2}OC$,所以$M_{1}M_{3}=2OC$,因为$\angle A_{10}OM_{3}=67.5^{\circ}-45^{\circ}=22.5^{\circ}$,$\angle M_{3}A_{10}O = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,所以$\angle A_{10}OM_{3}=\angle M_{3}A_{10}O$,所以$A_{10}M_{3}=OM_{3}=\sqrt{2}OC$,所以$A_{10}C = OC+\sqrt{2}OC$,所以$A_{1}A_{10}=2A_{10}C = 2OC+2\sqrt{2}OC=(1+\sqrt{2})\cdot2OC$,所以$\frac{A_{1}A_{10}}{M_{1}M_{3}}=\frac{(1+\sqrt{2})\cdot2OC}{2OC}=1+\sqrt{2}$。

16.推理能力 某学习小组在探索“各内角都相等的圆内接多边形是不是正多边形”时,进行了如下讨论:
甲同学:“这种多边形不一定是正多边形,如圆内接矩形.”
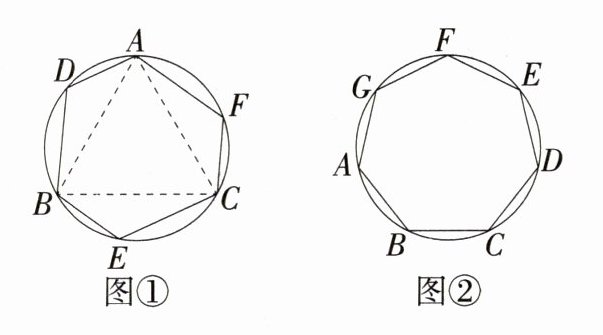
乙同学:“我发现圆内接多边形的边数是6时,它也不一定是正多边形,如图①,△ABC是正三角形,$\overset{\frown}{AD}=\overset{\frown}{BE}=\overset{\frown}{CF}$,可证明六边形ADBECF的各内角相等,但它不是正六边形.”
丙同学:“我能证明边数是5时,它是正多边形,我想边数是7时,它可能也是正多边形.”
(1)请你证明乙同学构造的六边形各内角相等.
(2)请你证明各内角都相等的圆内接七边形ABCDEFG(如图②)是正七边形.
(3)根据以上探索过程,提出你的猜想(不必证明).
甲同学:“这种多边形不一定是正多边形,如圆内接矩形.”
乙同学:“我发现圆内接多边形的边数是6时,它也不一定是正多边形,如图①,△ABC是正三角形,$\overset{\frown}{AD}=\overset{\frown}{BE}=\overset{\frown}{CF}$,可证明六边形ADBECF的各内角相等,但它不是正六边形.”
丙同学:“我能证明边数是5时,它是正多边形,我想边数是7时,它可能也是正多边形.”
(1)请你证明乙同学构造的六边形各内角相等.
(2)请你证明各内角都相等的圆内接七边形ABCDEFG(如图②)是正七边形.
(3)根据以上探索过程,提出你的猜想(不必证明).

答案:
解析:
(1)证明:由题图①知$\angle AFC$所对的弧是$\overset{\frown}{ABC}$,因为$\overset{\frown}{CF}=\overset{\frown}{DA}$,所以$\overset{\frown}{DEF}=\overset{\frown}{DBC}+\overset{\frown}{FC}=\overset{\frown}{DBC}+\overset{\frown}{AD}=\overset{\frown}{ABC}$,所以$\angle AFC=\angle DAF$。同理可证$\angle BDA=\angle DBE=\angle BEC=\angle ECF=\angle AFC$。故乙同学构造的六边形各内角相等。
(2)证明:因为$\angle A$所对的弧是$\overset{\frown}{BEG}$,$\angle B$所对的弧是$\overset{\frown}{CEA}$,$\angle A=\angle B$,所以$\overset{\frown}{BEG}=\overset{\frown}{CEA}$,所以$\overset{\frown}{BC}=\overset{\frown}{AG}$,同理可证得$\overset{\frown}{BA}=\overset{\frown}{CD}=\overset{\frown}{EF}=\overset{\frown}{AG}=\overset{\frown}{DE}=\overset{\frown}{FG}$,所以$BA = CD = EF = AG = BC = DE = FG$,所以各内角都相等的圆内接七边形ABCDEFG是正七边形。
(3)猜想:当边数是3,5,7,9,…时,各内角都相等的圆内接多边形是正多边形。当边数是4,6,8,10,…时,各内角都相等的圆内接多边形不一定是正多边形。
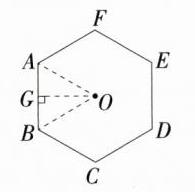
1.(2024四川泸州龙马潭二模)一个正六边形的边长为6,则它的边心距是( )
A.3
B.3$\sqrt{2}$
C.3$\sqrt{3}$
D.12
A.3
B.3$\sqrt{2}$
C.3$\sqrt{3}$
D.12
答案:
C:如图,正六边形的中心是O,过O作$OG\perp AB$于G,则$\angle AOB=\frac{360^{\circ}}{6}=60^{\circ}$,因为$AB = 6$,$OA = OB$,所以$\triangle OAB$为等边三角形,所以$AG=\frac{1}{2}AB = 3$,$OA = AB = 6$,所以$OG=\sqrt{AO^{2}-AG^{2}}=3\sqrt{3}$,即边心距是$3\sqrt{3}$。故选C。
C:如图,正六边形的中心是O,过O作$OG\perp AB$于G,则$\angle AOB=\frac{360^{\circ}}{6}=60^{\circ}$,因为$AB = 6$,$OA = OB$,所以$\triangle OAB$为等边三角形,所以$AG=\frac{1}{2}AB = 3$,$OA = AB = 6$,所以$OG=\sqrt{AO^{2}-AG^{2}}=3\sqrt{3}$,即边心距是$3\sqrt{3}$。故选C。

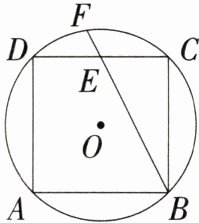
2.(2024福建南安模拟)如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为2$\sqrt{2}$,则EF的长度为( )
A.$\frac{2\sqrt{5}}{5}$
B.$\sqrt{2}$
C.1
D.$\frac{\sqrt{3}}{3}$

A.$\frac{2\sqrt{5}}{5}$
B.$\sqrt{2}$
C.1
D.$\frac{\sqrt{3}}{3}$
答案:
A:如图,连接OC,OE,DF,因为正方形ABCD内接于$\odot O$,点E是CD的中点,所以$\angle OCE=\frac{1}{2}\angle BCD = 45^{\circ}$,$OE\perp CD$,所以在$Rt\triangle OCE$中,$OE = CE = DE=\frac{\sqrt{2}}{2}OC = 2$。在$Rt\triangle BCE$中,$BC = CD = 2CE = 4$,所以$BE=\sqrt{BC^{2}+CE^{2}}=2\sqrt{5}$,因为$\angle FDC=\angle FBC$,$\angle DFE=\angle DCB$,所以$\triangle DEF\sim\triangle BEC$,所以$\frac{EF}{EC}=\frac{DE}{BE}$,即$DE\cdot EC=BE\cdot EF$,所以$2\times2 = 2\sqrt{5}\cdot EF$,所以$EF=\frac{2\sqrt{5}}{5}$。故选A。
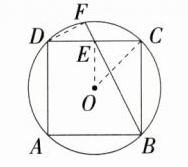
A:如图,连接OC,OE,DF,因为正方形ABCD内接于$\odot O$,点E是CD的中点,所以$\angle OCE=\frac{1}{2}\angle BCD = 45^{\circ}$,$OE\perp CD$,所以在$Rt\triangle OCE$中,$OE = CE = DE=\frac{\sqrt{2}}{2}OC = 2$。在$Rt\triangle BCE$中,$BC = CD = 2CE = 4$,所以$BE=\sqrt{BC^{2}+CE^{2}}=2\sqrt{5}$,因为$\angle FDC=\angle FBC$,$\angle DFE=\angle DCB$,所以$\triangle DEF\sim\triangle BEC$,所以$\frac{EF}{EC}=\frac{DE}{BE}$,即$DE\cdot EC=BE\cdot EF$,所以$2\times2 = 2\sqrt{5}\cdot EF$,所以$EF=\frac{2\sqrt{5}}{5}$。故选A。

3.(2023广西浦北期末)已知正三角形ABC的边心距为$\sqrt{3}$ cm,则正三角形的边长为_______cm.
答案:
答案:6 解析:如图所示,$\odot O$为$\triangle ABC$的外接圆,在正三角形ABC中,$OD\perp BC$,由题意可得,$OD=\sqrt{3}cm$,连接BO,易知$\angle OBD = 30^{\circ}$,所以$BD=\frac{OD}{\tan30^{\circ}}=3cm$,所以$BC = 2BD = 2\times3 = 6(cm)$。
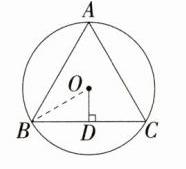
答案:6 解析:如图所示,$\odot O$为$\triangle ABC$的外接圆,在正三角形ABC中,$OD\perp BC$,由题意可得,$OD=\sqrt{3}cm$,连接BO,易知$\angle OBD = 30^{\circ}$,所以$BD=\frac{OD}{\tan30^{\circ}}=3cm$,所以$BC = 2BD = 2\times3 = 6(cm)$。

查看更多完整答案,请扫码查看


