《2025年5年中考3年模拟九年级数学下册沪科版》

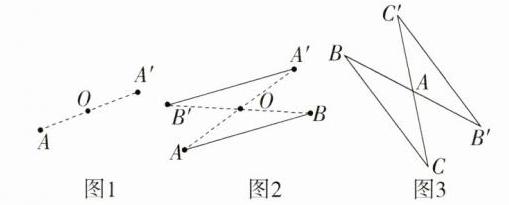
1.(2024山东招远期末)如图，$\triangle ABC$与$\triangle A'B'C'$关于点$O$成中心对称，则下列结论不一定成立的是(M9224002) （ ）


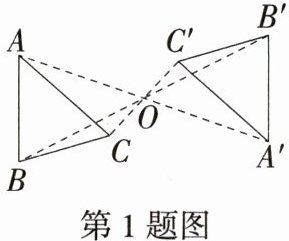
A.点$A$与点$A'$是对应点
B.$AO = A'O$
C.$\angle AOB = \angle A'OB'$
D.$\angle ACB = \angle C'A'B'$

答案： D

∵ △ABC与△A'B'C'关于点O成中心对称，
∴ 点A与点A'是对应点，AO = A'O，∠AOB = ∠A'OB'，
∴ A，B，C中结论都成立，不合题意.
∵ ∠ACB与∠C'A'B'不是对应角，
∴ ∠ACB = ∠C'A'B'不一定成立. 故选D.

2.新独家原创 如图，点$A$、点$A'$关于点$O$对称，点$B$、点$B'$关于点$O$对称，若$\angle OAB = 90^{\circ}$，$\angle OB'A' = 30^{\circ}$，$OA = 1$，则$BB'$的长为________.(M9224002)

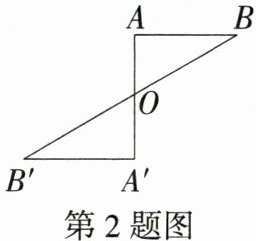
答案： 答案 4 解析 由点A、点A'关于点O对称，点B、点B'关于点O对称，可知OA = OA'，OB = OB'，B，O，B'共线. 易证△ABO ≌ △A'B'O，
∴ ∠ABO = ∠OB'A' = 30°，
∵ ∠OAB = 90°，OA = 1，
∴ OB = 2OA = 2，
∴ BB' = 2OB = 4.

3.(1)如图1，作出点$A$关于点$O$成中心对称的点$A'$.
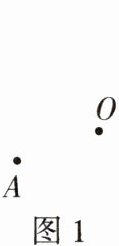
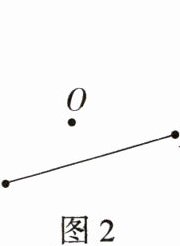
(2)如图2，作出线段$AB$关于点$O$成中心对称的线段$A'B'$.
(3)如图3，作出$\triangle ABC$关于点$A$成中心对称的$\triangle AB'C'$.
(4)在(3)作出的图形中，请说明点$C$，$A$，$C'$的位置关系.

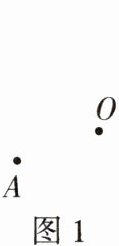
答案：
解析 （1）如图1，A'即为点A关于点O成中心对称的点. （2）如图2，A'B'即为线段AB关于点O成中心对称的线段. （3）如图3，△AB'C'即为△ABC关于点A成中心对称的图形. 

（4）点C，A，C'在同一条直线上，且点C与点C'到点A的距离相等.

4.情境题·现实生活 (2024安徽潜山开学测)下列交通标志中，是中心对称图形的是(M9224004) （ ）

答案： A 绕某一个定点旋转180°后能与自身重合的只有A中的图形，故选A. 方法归纳 一般地，如果倒看看到的图形与正看看到的图形一样，那么这个图形是中心对称图形.

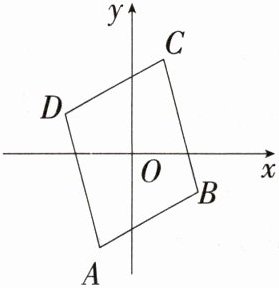
5.(2023浙江温州实验中学期中)如图，在平面直角坐标系中，$\square ABCD$的对称中心是坐标原点，顶点$A$的坐标是$(-1,-3)$，则顶点$C$的坐标是________.(M9224003)

答案： 答案 （1，3） 解析
∵ 平行四边形ABCD的对称中心是坐标原点，且点A的坐标是（-1，-3），
∴ 点C的坐标是（1，3）.

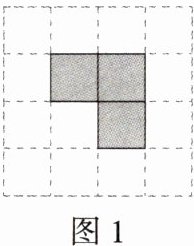
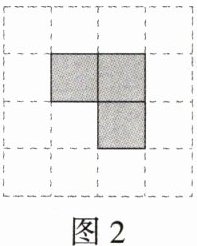
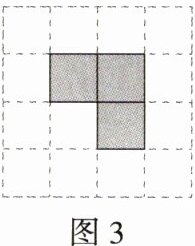
6.(2024安徽淮南龙湖中学期中)在由小正方形组成的$4\times4$的网格中，$3$个阴影小正方形组成如图所示的图形，按下列要求在各网格图中补上一个阴影小正方形.
(1)使图1中的阴影小正方形组成轴对称图形但不是中心对称图形.
(2)使图2中的阴影小正方形组成中心对称图形但不是轴对称图形.
(3)使图3中的阴影小正方形组成的图形既是轴对称图形又是中心对称图形.

答案：
解析 （1）如图所示.（答案不唯一）

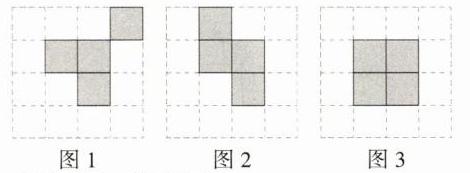
（2）如图所示.（答案不唯一） （3）如图所示.