第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024广西柳州柳南铁五中学期中)如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD = 110°,则∠DCE的大小是( )
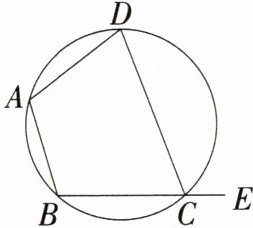
A.70°
B.105°
C.110°
D.120°

A.70°
B.105°
C.110°
D.120°
答案:
C 因为四边形ABCD是圆内接四边形,所以∠DCE = ∠BAD = 110°,故选C。
2.四边形ABCD内接于⊙O,且∠A = ∠C,∠B = ∠D,则四边形ABCD是(M9224007) ( )
A.平行四边形
B.矩形
C.菱形
D.正方形
A.平行四边形
B.矩形
C.菱形
D.正方形
答案:
B 因为四边形ABCD内接于⊙O,所以∠A + ∠C = 180°,∠B + ∠D = 180°。又∠A = ∠C,∠B = ∠D,所以∠A = ∠B = ∠C = ∠D = 90°,所以四边形ABCD是矩形。
3.新独家原创 如图,四边形ABOC内接于⊙E,以O为原点建立平面直角坐标系,点B、D的坐标分别为(-$\sqrt{3}$,0),(0,1),若∠C = 110°,则∠ABD的度数为_________.(M9224007)


答案:
答案 40°
解析 因为∠BOD = 90°,所以BD是直径。因为点B、D的坐标分别为(-√3, 0),(0, 1),所以OB = √3,OD = 1。在Rt△BOD中,tan∠OBD = $\frac{OD}{OB}=\frac{\sqrt{3}}{3}$,所以∠OBD = 30°。因为∠C = 110°,∠C + ∠ABO = 180°,所以∠ABO = 180° - 110° = 70°,所以∠ABD = 70° - 30° = 40°。
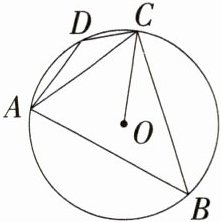
4.(2024安徽滁州定远一中开学测)如图,四边形ABCD内接于⊙O,OC = 4,AC = 4$\sqrt{2}$.(M9224007)
(1)求点O到AC的距离.
(2)求∠ADC的度数.
(1)求点O到AC的距离.
(2)求∠ADC的度数.

答案:
解析
(1) 如图,作OM⊥AC于M,因为AC = 4√2,所以AM = CM = 2√2。因为OC = 4,所以OM = $\sqrt{OC^{2}-MC^{2}} = 2\sqrt{2}$。
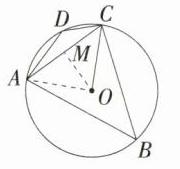
(2) 如图,连接OA,因为OM = MC,∠OMC = 90°,所以∠MOC = ∠MCO = 45°,因为OA = OC,所以∠OAM = 45°,所以∠AOC = 90°,所以∠B = 45°,因为∠D + ∠B = 180°,所以∠D = 135°。
解析
(1) 如图,作OM⊥AC于M,因为AC = 4√2,所以AM = CM = 2√2。因为OC = 4,所以OM = $\sqrt{OC^{2}-MC^{2}} = 2\sqrt{2}$。

(2) 如图,连接OA,因为OM = MC,∠OMC = 90°,所以∠MOC = ∠MCO = 45°,因为OA = OC,所以∠OAM = 45°,所以∠AOC = 90°,所以∠B = 45°,因为∠D + ∠B = 180°,所以∠D = 135°。
5.(2024四川宜宾中考,9,★★☆)如图,△ABC内接于⊙O,BC为⊙O的直径,AD平分∠BAC交⊙O于D,则$\frac{AB + AC}{AD}$的值为 ( )
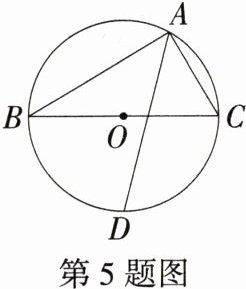
A.$\sqrt{2}$
B.$\sqrt{3}$
C.2$\sqrt{2}$
D.2$\sqrt{3}$

A.$\sqrt{2}$
B.$\sqrt{3}$
C.2$\sqrt{2}$
D.2$\sqrt{3}$
答案:
A 如图,连接BD、CD,因为BC是⊙O的直径,所以∠BAC = ∠BDC = 90°。因为AD平分∠BAC,所以∠BAD = ∠CAD,所以$\overset{\frown}{BD}=\overset{\frown}{DC}$,所以BD = CD。在四边形ABDC中,∠BAC = ∠BDC = 90°,∠ACD + ∠ABD = 180°,将△ADC绕D点逆时针旋转90°,设A旋转后的对应点为A',易证A,B,A'三点共线,CD旋转至BD处,AD旋转至A'D处,如图所示,可知AB + AC = AB + A'B = AA'。由旋转可知∠A'DB = ∠ADC,A'D = AD,所以∠A'DA = ∠A'DB + ∠BDA = ∠ADC + ∠BDA = ∠BDC = 90°,所以在等腰直角三角形A'DA中,sin A' = sin 45° = $\frac{AD}{AA'}=\frac{\sqrt{2}}{2}$,所以$\frac{AB + AC}{AD}=\frac{AA'}{AD}=\sqrt{2}$,故选A。
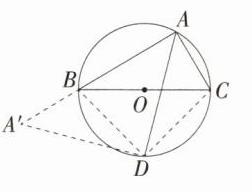
A 如图,连接BD、CD,因为BC是⊙O的直径,所以∠BAC = ∠BDC = 90°。因为AD平分∠BAC,所以∠BAD = ∠CAD,所以$\overset{\frown}{BD}=\overset{\frown}{DC}$,所以BD = CD。在四边形ABDC中,∠BAC = ∠BDC = 90°,∠ACD + ∠ABD = 180°,将△ADC绕D点逆时针旋转90°,设A旋转后的对应点为A',易证A,B,A'三点共线,CD旋转至BD处,AD旋转至A'D处,如图所示,可知AB + AC = AB + A'B = AA'。由旋转可知∠A'DB = ∠ADC,A'D = AD,所以∠A'DA = ∠A'DB + ∠BDA = ∠ADC + ∠BDA = ∠BDC = 90°,所以在等腰直角三角形A'DA中,sin A' = sin 45° = $\frac{AD}{AA'}=\frac{\sqrt{2}}{2}$,所以$\frac{AB + AC}{AD}=\frac{AA'}{AD}=\sqrt{2}$,故选A。

6.(2024山东滨州中考,14,★★☆)如图,四边形ABCD内接于⊙O,若四边形OABC是菱形,则∠D = _________°.


答案:
答案 60
解析 设∠D = x°,因为四边形ABCD内接于⊙O,所以∠B + ∠D = 180°。因为四边形OABC是菱形,所以∠AOC = ∠B。又∠AOC = 2∠D = 2x°,所以2x + x = 180,解得x = 60,即∠D = 60°。
7.(2024安徽合肥长丰一模,20,★★☆)如图,四边形ABCD内接于⊙O,∠BAD = 90°,BC = CD,过点C作CE,使得CD = CE,且E在AD的延长线上.
(1)求证:AB = AE.
(2)若AD = DE = 2,求CD的长.
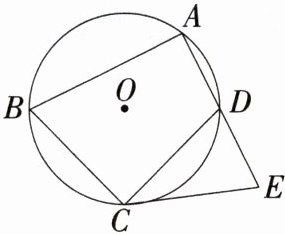
(1)求证:AB = AE.
(2)若AD = DE = 2,求CD的长.

答案:
解析
(1) **证明**:如图1,连接AC。因为BC = CD,所以$\overset{\frown}{BC}=\overset{\frown}{CD}$,所以∠BAC = ∠EAC。因为CD = CE,所以∠E = ∠CDE,BC = CE。因为∠B + ∠ADC = 180°,∠CDE + ∠ADC = 180°,所以∠B = ∠CDE,所以∠B = ∠E。在△ABC与△AEC中,$\begin{cases}∠BAC = ∠EAC \\∠B = ∠E \\BC = EC\end{cases}$,所以△ABC≌△AEC(AAS),所以AB = AE。
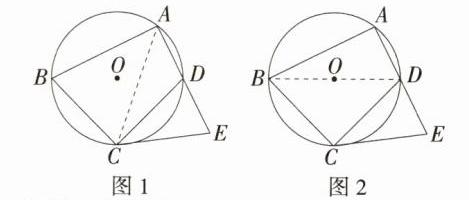
(2) 如图2,连接BD。因为∠BAD = 90°,所以BD是⊙O的直径,所以∠BCD = 90°。由
(1)可得AB = AE。因为AD = DE = 2,所以AB = AE = AD + DE = 4。在Rt△ABD中,BD = $\sqrt{AB^{2}+AD^{2}} = 2\sqrt{5}$。在Rt△BCD中,CD = BC = $\frac{\sqrt{2}}{2}BD=\sqrt{10}$。
解析
(1) **证明**:如图1,连接AC。因为BC = CD,所以$\overset{\frown}{BC}=\overset{\frown}{CD}$,所以∠BAC = ∠EAC。因为CD = CE,所以∠E = ∠CDE,BC = CE。因为∠B + ∠ADC = 180°,∠CDE + ∠ADC = 180°,所以∠B = ∠CDE,所以∠B = ∠E。在△ABC与△AEC中,$\begin{cases}∠BAC = ∠EAC \\∠B = ∠E \\BC = EC\end{cases}$,所以△ABC≌△AEC(AAS),所以AB = AE。

(2) 如图2,连接BD。因为∠BAD = 90°,所以BD是⊙O的直径,所以∠BCD = 90°。由
(1)可得AB = AE。因为AD = DE = 2,所以AB = AE = AD + DE = 4。在Rt△ABD中,BD = $\sqrt{AB^{2}+AD^{2}} = 2\sqrt{5}$。在Rt△BCD中,CD = BC = $\frac{\sqrt{2}}{2}BD=\sqrt{10}$。
查看更多完整答案,请扫码查看


