第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
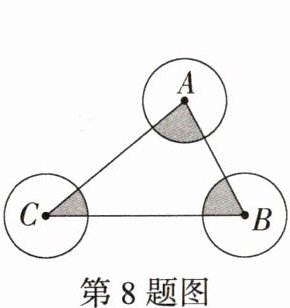
8.教材变式·P57T5 如图,⊙A,⊙B,⊙C的半径都是2,则图中三个扇形(即阴影部分)的面积之和是 ( )
A.2π
B.π
C.$\frac{1}{2}\pi$
D.6π

A.2π
B.π
C.$\frac{1}{2}\pi$
D.6π
答案:
A:$\because$三角形的内角和等于$180^{\circ}$,$\therefore$三个扇形的圆心角度数之和等于$180^{\circ}$,又$\because$三个扇形的半径都是$2$,$\therefore$三个扇形的面积之和为$\frac{180\pi\times2^{2}}{360}=2\pi$,故选A。
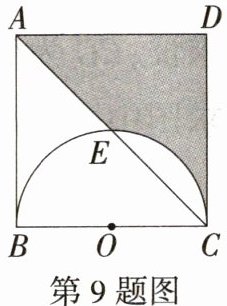
9.一题多解 (2024四川岳池三模)如图,正方形ABCD的边长为2,以BC为直径的半圆与对角线AC相交于点E,则图中阴影部分的面积为(M9224013) ( )
A.$\frac{5}{2}+\frac{\pi}{4}$
B.$\frac{3}{2}-\frac{\pi}{4}$
C.$\frac{5}{2}-\frac{\pi}{2}$
D.$\frac{5}{2}-\frac{\pi}{4}$

A.$\frac{5}{2}+\frac{\pi}{4}$
B.$\frac{3}{2}-\frac{\pi}{4}$
C.$\frac{5}{2}-\frac{\pi}{2}$
D.$\frac{5}{2}-\frac{\pi}{4}$
答案:
D: 【解法一】如图,连接$OE$。由题意知$OE = OC = 1$。$\because S_{\triangle ADC}=\frac{1}{2}AD\cdot CD=\frac{1}{2}\times2\times2 = 2$,$S_{扇形COE}=\frac{1}{4}\pi\times1^{2}=\frac{\pi}{4}$,$S_{\triangle COE}=\frac{1}{2}\times1\times1=\frac{1}{2}$,$\therefore$阴影部分的面积为$2 - (\frac{\pi}{4}-\frac{1}{2})=\frac{5}{2}-\frac{\pi}{4}$。故选D。 【解法二】如图,连接$OE$。由题意知$OE = OC = 1$,$\therefore S_{阴影}=S_{正方形ABCD}-S_{扇形COE}-S_{四边形ABOE}=2^{2}-\frac{1}{4}\pi\times1^{2}-\frac{1}{2}\times(1 + 2)\times1=\frac{5}{2}-\frac{\pi}{4}$。故选D。
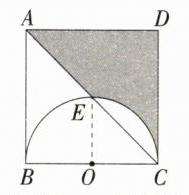
D: 【解法一】如图,连接$OE$。由题意知$OE = OC = 1$。$\because S_{\triangle ADC}=\frac{1}{2}AD\cdot CD=\frac{1}{2}\times2\times2 = 2$,$S_{扇形COE}=\frac{1}{4}\pi\times1^{2}=\frac{\pi}{4}$,$S_{\triangle COE}=\frac{1}{2}\times1\times1=\frac{1}{2}$,$\therefore$阴影部分的面积为$2 - (\frac{\pi}{4}-\frac{1}{2})=\frac{5}{2}-\frac{\pi}{4}$。故选D。 【解法二】如图,连接$OE$。由题意知$OE = OC = 1$,$\therefore S_{阴影}=S_{正方形ABCD}-S_{扇形COE}-S_{四边形ABOE}=2^{2}-\frac{1}{4}\pi\times1^{2}-\frac{1}{2}\times(1 + 2)\times1=\frac{5}{2}-\frac{\pi}{4}$。故选D。

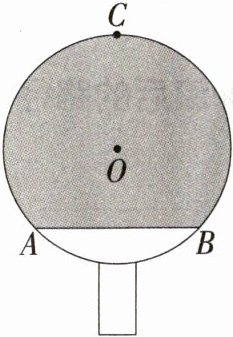
10.跨体育与健康·乒乓球拍 和差法求面积 我国的国球是乒乓球,世界上乒乓球拍的拍形大体上可以归为三类:圆形、方形和异形,绝大多数的横板与中国式的直板都是圆形的.如图所示的是李明同学自制的一块乒乓球拍,⊙O的半径为8 cm,$\overset{\frown}{AB}$的长为4π cm,弓形ACB(阴影部分)粘贴胶皮,则胶皮的面积为________cm².

答案:
答案:$(32 + 48\pi)$ 解析:如图,连接$OA$、$OB$,设$\angle AOB$的度数为$n^{\circ}$,$\because\overset{\frown}{AB}$的长为$4\pi\ cm$,$OB = 8\ cm$,$\therefore\frac{n\pi\times8}{180}=4\pi$,$\therefore n = 90$,$\therefore\angle AOB = 90^{\circ}$,$\therefore S_{\triangle AOB}=\frac{1}{2}\times8\times8 = 32(cm^{2})$,$\overset{\frown}{ACB}$的度数为$270^{\circ}$,$\therefore\overset{\frown}{ACB}$与$OA$、$OB$围成的扇形的面积$=\frac{270\times\pi\times8^{2}}{360}=48\pi(cm^{2})$,则胶皮的面积为$(32 + 48\pi)cm^{2}$。

答案:$(32 + 48\pi)$ 解析:如图,连接$OA$、$OB$,设$\angle AOB$的度数为$n^{\circ}$,$\because\overset{\frown}{AB}$的长为$4\pi\ cm$,$OB = 8\ cm$,$\therefore\frac{n\pi\times8}{180}=4\pi$,$\therefore n = 90$,$\therefore\angle AOB = 90^{\circ}$,$\therefore S_{\triangle AOB}=\frac{1}{2}\times8\times8 = 32(cm^{2})$,$\overset{\frown}{ACB}$的度数为$270^{\circ}$,$\therefore\overset{\frown}{ACB}$与$OA$、$OB$围成的扇形的面积$=\frac{270\times\pi\times8^{2}}{360}=48\pi(cm^{2})$,则胶皮的面积为$(32 + 48\pi)cm^{2}$。

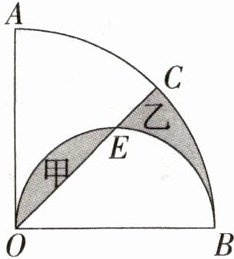
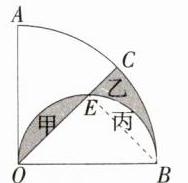
11.割补法求面积 如图,在扇形AOB中,∠AOB = 90°,∠COB = 45°,在半圆OEB中,OB = 10,求图中阴影部分的面积.(M9224013)

答案:
解析:如图,连接$BE$。$\because OB$为半圆$OEB$的直径,$\therefore\angle OEB = 90^{\circ}$,$\because\angle EOB = 45^{\circ}$,$\therefore\angle OBE = 45^{\circ}$,$\therefore OE = BE$,$\therefore S_{甲}=S_{丙}$,$\therefore S_{阴影}=S_{甲}+S_{乙}=S_{丙}+S_{乙}=S_{扇形BOC}-S_{\triangle OEB}$,$\because OB = 10$,$\therefore OE = BE = 5\sqrt{2}$,$\therefore S_{阴影}=\frac{45\pi\times10^{2}}{360}-\frac{1}{2}\times5\sqrt{2}\times5\sqrt{2}=\frac{25}{2}\pi - 25$。
解析:如图,连接$BE$。$\because OB$为半圆$OEB$的直径,$\therefore\angle OEB = 90^{\circ}$,$\because\angle EOB = 45^{\circ}$,$\therefore\angle OBE = 45^{\circ}$,$\therefore OE = BE$,$\therefore S_{甲}=S_{丙}$,$\therefore S_{阴影}=S_{甲}+S_{乙}=S_{丙}+S_{乙}=S_{扇形BOC}-S_{\triangle OEB}$,$\because OB = 10$,$\therefore OE = BE = 5\sqrt{2}$,$\therefore S_{阴影}=\frac{45\pi\times10^{2}}{360}-\frac{1}{2}\times5\sqrt{2}\times5\sqrt{2}=\frac{25}{2}\pi - 25$。

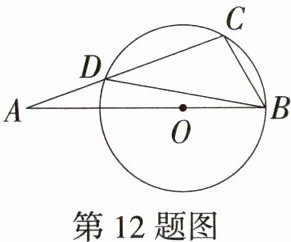
12.(2024安徽合肥瑶海三模,7,★★☆)如图,△ABC的顶点B,C落在⊙O上,AB经过圆心O,AC与⊙O相交于点D,已知∠A = 20°,∠CBD = 50°,BC = 2,则$\overset{\frown}{CD}$的长为 ( )
A.$\frac{5\pi}{9}$
B.$\frac{10\pi}{9}$
C.π
D.$\frac{20\pi}{9}$

A.$\frac{5\pi}{9}$
B.$\frac{10\pi}{9}$
C.π
D.$\frac{20\pi}{9}$
答案:
B:连接$OC$,$OD$,$\because\angle CBD = 50^{\circ}$,$\therefore\angle COD = 100^{\circ}$。$\because OC = OD$,$\therefore\angle ODC=\angle OCD = 40^{\circ}$,$\therefore\angle DOA=\angle ODC-\angle A = 20^{\circ}$,$\therefore\angle BOC = 180^{\circ}-100^{\circ}-20^{\circ}=60^{\circ}$。$\because OC = OB$,$\therefore\triangle OBC$是等边三角形,$\therefore OC = BC = 2$,$\therefore\overset{\frown}{CD}$的长$=\frac{100\pi\times2}{180}=\frac{10\pi}{9}$。故选B。

B:连接$OC$,$OD$,$\because\angle CBD = 50^{\circ}$,$\therefore\angle COD = 100^{\circ}$。$\because OC = OD$,$\therefore\angle ODC=\angle OCD = 40^{\circ}$,$\therefore\angle DOA=\angle ODC-\angle A = 20^{\circ}$,$\therefore\angle BOC = 180^{\circ}-100^{\circ}-20^{\circ}=60^{\circ}$。$\because OC = OB$,$\therefore\triangle OBC$是等边三角形,$\therefore OC = BC = 2$,$\therefore\overset{\frown}{CD}$的长$=\frac{100\pi\times2}{180}=\frac{10\pi}{9}$。故选B。

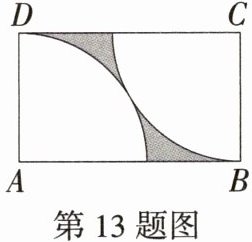
13.(2024重庆中考A卷,8,★★☆)如图,在矩形ABCD中,分别以点A和C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD = 4,则图中阴影部分的面积为 ( )
A.32 - 8π
B.16$\sqrt{3}$ - 4π
C.32 - 4π
D.16$\sqrt{3}$ - 8π

A.32 - 8π
B.16$\sqrt{3}$ - 4π
C.32 - 4π
D.16$\sqrt{3}$ - 8π
答案:
D:如图,连接$AC$。$\because$两弧有且仅有一个公共点,$AD = 4$,$\therefore AC = 2AD = 8$,$\therefore$在$Rt\triangle ADC$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$,$\therefore S_{矩形ABCD}=AD\cdot CD = 16\sqrt{3}$,$\because$两个扇形均为$\frac{1}{4}$圆,而且它们的半径相等,$\therefore$两个扇形面积之和为$\frac{1}{2}$圆,即$S_{两个扇形}=\frac{1}{2}\pi AD^{2}=8\pi$,$\therefore S_{阴影}=S_{矩形ABCD}-S_{两个扇形}=16\sqrt{3}-8\pi$。故选D。
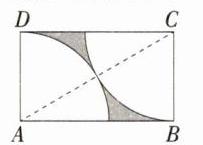
D:如图,连接$AC$。$\because$两弧有且仅有一个公共点,$AD = 4$,$\therefore AC = 2AD = 8$,$\therefore$在$Rt\triangle ADC$中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$,$\therefore S_{矩形ABCD}=AD\cdot CD = 16\sqrt{3}$,$\because$两个扇形均为$\frac{1}{4}$圆,而且它们的半径相等,$\therefore$两个扇形面积之和为$\frac{1}{2}$圆,即$S_{两个扇形}=\frac{1}{2}\pi AD^{2}=8\pi$,$\therefore S_{阴影}=S_{矩形ABCD}-S_{两个扇形}=16\sqrt{3}-8\pi$。故选D。

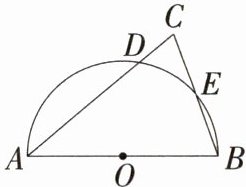
14.(2024四川广安中考,9,★★☆)如图,在等腰三角形ABC中,AB = AC = 10,∠C = 70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则$\overset{\frown}{DE}$的长度为(M9224013) ( )
A.$\frac{\pi}{9}$
B.$\frac{5\pi}{9}$
C.$\frac{10\pi}{9}$
D.$\frac{25\pi}{9}$

A.$\frac{\pi}{9}$
B.$\frac{5\pi}{9}$
C.$\frac{10\pi}{9}$
D.$\frac{25\pi}{9}$
答案:
C:如图,连接$OD$,$OE$,$\because AB = AC$,$\therefore\angle ABC=\angle C = 70^{\circ}$,$\because OE = OB$,$\therefore\angle OEB=\angle ABC = 70^{\circ}$,$\therefore\angle OEB=\angle C = 70^{\circ}$,$\therefore OE// AC$,在$\triangle ABC$中,$\angle A+\angle ABC+\angle C = 180^{\circ}$,$\therefore\angle A = 180^{\circ}-\angle ABC-\angle C = 180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$,$\because OA = OD=\frac{1}{2}AB = 5$,$OE// AC$,$\therefore\angle A=\angle ADO = 40^{\circ}=\angle DOE$,$\therefore\overset{\frown}{DE}$的长度为$\frac{40\pi\times5}{180}=\frac{10\pi}{9}$,故选C。

C:如图,连接$OD$,$OE$,$\because AB = AC$,$\therefore\angle ABC=\angle C = 70^{\circ}$,$\because OE = OB$,$\therefore\angle OEB=\angle ABC = 70^{\circ}$,$\therefore\angle OEB=\angle C = 70^{\circ}$,$\therefore OE// AC$,在$\triangle ABC$中,$\angle A+\angle ABC+\angle C = 180^{\circ}$,$\therefore\angle A = 180^{\circ}-\angle ABC-\angle C = 180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$,$\because OA = OD=\frac{1}{2}AB = 5$,$OE// AC$,$\therefore\angle A=\angle ADO = 40^{\circ}=\angle DOE$,$\therefore\overset{\frown}{DE}$的长度为$\frac{40\pi\times5}{180}=\frac{10\pi}{9}$,故选C。

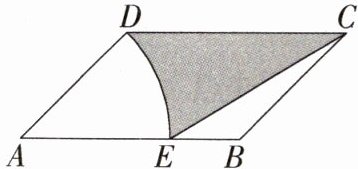
15.和差法求面积 (2022广西贵港中考,17,★★☆)如图,在□ABCD中,AD = $\frac{2}{3}$AB,∠BAD = 45°,以点A为圆心,AD长为半径画弧交AB于点E,连接CE,若AB = 3$\sqrt{2}$,则图中阴影部分的面积是________.

答案:
答案:$5\sqrt{2}-\pi$ 解析:如图,过点$D$作$DF\perp AB$于点$F$,$\because AD=\frac{2}{3}AB$,$AB = 3\sqrt{2}$,$\therefore AD=\frac{2}{3}\times3\sqrt{2}=2\sqrt{2}$,$\because\angle BAD = 45^{\circ}$,$\therefore DF = AD\cdot\sin45^{\circ}=2\sqrt{2}\times\frac{\sqrt{2}}{2}=2$,$\because AE = AD = 2\sqrt{2}$,$\therefore EB = AB - AE=\sqrt{2}$,$\therefore S_{阴影}=S_{\square ABCD}-S_{扇形DAE}-S_{\triangle EBC}=3\sqrt{2}\times2-\frac{45\pi\times(2\sqrt{2})^{2}}{360}-\frac{1}{2}\times\sqrt{2}\times2=5\sqrt{2}-\pi$。
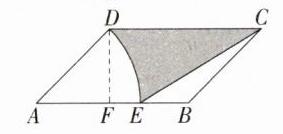
答案:$5\sqrt{2}-\pi$ 解析:如图,过点$D$作$DF\perp AB$于点$F$,$\because AD=\frac{2}{3}AB$,$AB = 3\sqrt{2}$,$\therefore AD=\frac{2}{3}\times3\sqrt{2}=2\sqrt{2}$,$\because\angle BAD = 45^{\circ}$,$\therefore DF = AD\cdot\sin45^{\circ}=2\sqrt{2}\times\frac{\sqrt{2}}{2}=2$,$\because AE = AD = 2\sqrt{2}$,$\therefore EB = AB - AE=\sqrt{2}$,$\therefore S_{阴影}=S_{\square ABCD}-S_{扇形DAE}-S_{\triangle EBC}=3\sqrt{2}\times2-\frac{45\pi\times(2\sqrt{2})^{2}}{360}-\frac{1}{2}\times\sqrt{2}\times2=5\sqrt{2}-\pi$。

查看更多完整答案,请扫码查看


