第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,如果OE = OF,那么下列结论不一定正确的是 ( )
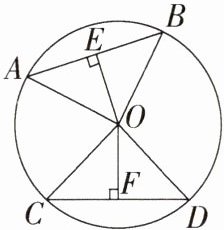
A.∠AOB = ∠COD
B.AB = CD
C.∠AOC = ∠BOD
D.$\overset{\frown}{AB}=\overset{\frown}{CD}$

A.∠AOB = ∠COD
B.AB = CD
C.∠AOC = ∠BOD
D.$\overset{\frown}{AB}=\overset{\frown}{CD}$
答案:
C 由OE = OF,OE⊥AB,OF⊥CD,可得AB = CD,∠AOB = ∠COD,$\overset{\frown}{AB}=\overset{\frown}{CD}$,但∠AOC与∠BOD不一定相等,故选C.
2.一题多解 如图,四边形ABCD的顶点都在⊙O上,AB是直径,且AB//CD,若∠D = 120°,AD = 2 cm,则CD = ________ cm.(M9224005)
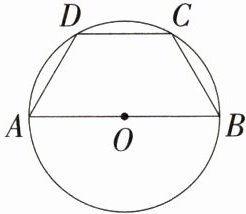

答案:
答案 2 解析 【解法一】如图①,连接OD,OC.
∵AB//CD,
∴∠A + ∠ADC = 180°. 又
∵∠ADC = 120°,
∴∠A = 180° - 120° = 60°,
∵OA = OD,
∴△AOD是等边三角形,
∴∠ADO = 60°,
∴∠ODC = 60°. 又OC = OD,
∴△COD是等边三角形,
∴CD = OD = AD = 2 cm.【解法二】如图②,连接OD,过O作OE⊥AD,OF⊥CD,垂足分别为E,F.
∵AB//CD,
∴∠A + ∠ADC = 180°. 又
∵∠ADC = 120°,
∴∠A = 180° - 120° = 60°,
∵OA = OD,
∴∠ADO = 60°,
∴∠ODC = 60°,
∴OE = OD·sin 60° = OF,
∴CD = AD = 2 cm.
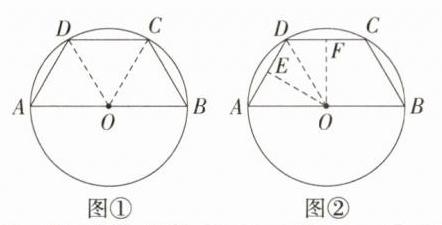
答案 2 解析 【解法一】如图①,连接OD,OC.
∵AB//CD,
∴∠A + ∠ADC = 180°. 又
∵∠ADC = 120°,
∴∠A = 180° - 120° = 60°,
∵OA = OD,
∴△AOD是等边三角形,
∴∠ADO = 60°,
∴∠ODC = 60°. 又OC = OD,
∴△COD是等边三角形,
∴CD = OD = AD = 2 cm.【解法二】如图②,连接OD,过O作OE⊥AD,OF⊥CD,垂足分别为E,F.
∵AB//CD,
∴∠A + ∠ADC = 180°. 又
∵∠ADC = 120°,
∴∠A = 180° - 120° = 60°,
∵OA = OD,
∴∠ADO = 60°,
∴∠ODC = 60°,
∴OE = OD·sin 60° = OF,
∴CD = AD = 2 cm.

3.(2024江苏南通通州期中)如图,在⊙O中,弦AB,CD相交于点E,AD = BC.(M9224005)
(1)比较$\overset{\frown}{AB}$与$\overset{\frown}{CD}$的长度,并证明你的结论.
(2)求证:AE = CE.
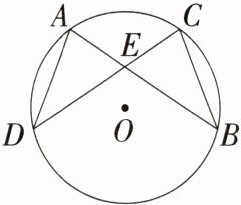
(1)比较$\overset{\frown}{AB}$与$\overset{\frown}{CD}$的长度,并证明你的结论.
(2)求证:AE = CE.

答案:
解析
(1)$\overset{\frown}{AB}$与$\overset{\frown}{CD}$的长度相等. 证明:
∵AD = BC,
∴$\overset{\frown}{AD}=\overset{\frown}{BC}$,
∴$\overset{\frown}{AD}+\overset{\frown}{AC}=\overset{\frown}{BC}+\overset{\frown}{AC}$,
∴$\overset{\frown}{CD}=\overset{\frown}{AB}$.
(2)证明:连接AC(图略), 由
(1)知$\overset{\frown}{CD}=\overset{\frown}{AB}$,
∴AB = CD, 在△ADC和△CBA中,$\begin{cases}AC = CA,\\CD = AB,\\AD = CB,\end{cases}$
∴△ADC≌△CBA(SSS),
∴∠ACD = ∠CAB,
∴AE = CE. ·方法归纳 证明弧相等,常通过说明这两条弧所对的圆心角相等,或所对的弦相等进行证明.
(1)$\overset{\frown}{AB}$与$\overset{\frown}{CD}$的长度相等. 证明:
∵AD = BC,
∴$\overset{\frown}{AD}=\overset{\frown}{BC}$,
∴$\overset{\frown}{AD}+\overset{\frown}{AC}=\overset{\frown}{BC}+\overset{\frown}{AC}$,
∴$\overset{\frown}{CD}=\overset{\frown}{AB}$.
(2)证明:连接AC(图略), 由
(1)知$\overset{\frown}{CD}=\overset{\frown}{AB}$,
∴AB = CD, 在△ADC和△CBA中,$\begin{cases}AC = CA,\\CD = AB,\\AD = CB,\end{cases}$
∴△ADC≌△CBA(SSS),
∴∠ACD = ∠CAB,
∴AE = CE. ·方法归纳 证明弧相等,常通过说明这两条弧所对的圆心角相等,或所对的弦相等进行证明.
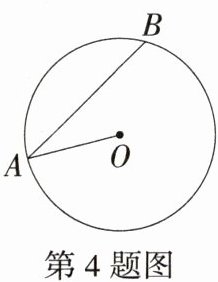
4.(2024甘肃武威凉州二模)如图,在⊙O中,∠A = 30°,则劣弧$\overset{\frown}{AB}$的度数是 ( )
A.30°
B.60°
C.90°
D.120°

A.30°
B.60°
C.90°
D.120°
答案:
D 连接OB(图略),
∵OA = OB,
∴∠B = ∠A = 30°,
∴∠AOB = 180° - 30° - 30° = 120°,
∴劣弧$\overset{\frown}{AB}$的度数为120°. 故选D.
∵OA = OB,
∴∠B = ∠A = 30°,
∴∠AOB = 180° - 30° - 30° = 120°,
∴劣弧$\overset{\frown}{AB}$的度数为120°. 故选D.
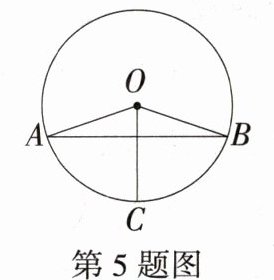
5.如图,半径OC⊥AB,$\overset{\frown}{BC}$的度数为70°,连接OA,OB,则∠AOC = ( )
A.20°
B.35°
C.55°
D.70°

A.20°
B.35°
C.55°
D.70°
答案:
D
∵$\overset{\frown}{BC}$的度数为70°,
∴∠BOC = 70°,
∵OC⊥AB,
∴$\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴∠AOC = ∠BOC = 70°. 故选D.
∵$\overset{\frown}{BC}$的度数为70°,
∴∠BOC = 70°,
∵OC⊥AB,
∴$\overset{\frown}{AC}=\overset{\frown}{BC}$,
∴∠AOC = ∠BOC = 70°. 故选D.
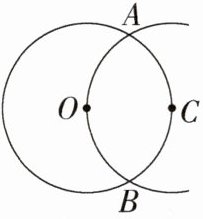
6.如图,点C是⊙O上的点,以点C为圆心,⊙O的半径为半径作弧交⊙O于点A、B,则$\overset{\frown}{ACB}$的度数为________.

答案:
答案 120°
解析 连接OA、OB、OC、AC、BC(图略),由题意可知CA = OC = OA,
∴△AOC是等边三角形,
∴∠AOC = 60°,同理∠BOC = 60°,则∠AOB = 120°,
∴$\overset{\frown}{ACB}$的度数为120°.
∴△AOC是等边三角形,
∴∠AOC = 60°,同理∠BOC = 60°,则∠AOB = 120°,
∴$\overset{\frown}{ACB}$的度数为120°.
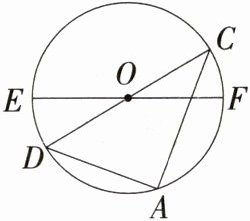
7.(2024安徽亳州二模,7,★★☆)如图,EF,CD是⊙O的两条直径,点A是劣弧$\overset{\frown}{DF}$的中点.若∠COF = 32°,则∠ADC的度数是 ( )
A.47°
B.74°
C.53°
D.63°

A.47°
B.74°
C.53°
D.63°
答案:
C 连接OA,如图.
∵∠COF = 32°,
∴∠DOF = 180° - 32° = 148°,
∵点A是劣弧$\overset{\frown}{DF}$的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{AF}$,则∠AOD = ∠AOF = $\frac{1}{2}$∠DOF = 74°.
∵OD = OA,
∴∠ADC = $\frac{180° - 74°}{2}$ = 53°,故选C
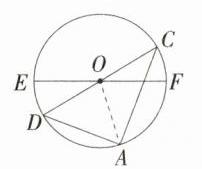
C 连接OA,如图.
∵∠COF = 32°,
∴∠DOF = 180° - 32° = 148°,
∵点A是劣弧$\overset{\frown}{DF}$的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{AF}$,则∠AOD = ∠AOF = $\frac{1}{2}$∠DOF = 74°.
∵OD = OA,
∴∠ADC = $\frac{180° - 74°}{2}$ = 53°,故选C

8.(2023安徽合肥庐阳一模,13,★★☆)如图,在△ABC中,∠B = 70°,⊙O截三边所得的弦长DE = FG = HI,则∠AOC = ________度.


答案:
答案 125 解析 过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE = FG = HI,
∴OM = OK = OP,
∴AO平分∠BAC,CO平分∠ACB,
∴∠OAC = $\frac{1}{2}$∠BAC,∠OCA = $\frac{1}{2}$∠BCA,
∵∠B = 70°,
∴∠BAC + ∠BCA = 180° - ∠B = 110°,
∴∠OAC + ∠OCA = $\frac{1}{2}$(∠BAC + ∠ACB) = $\frac{1}{2}$×110° = 55°,
∴∠AOC = 180° - (∠OAC + ∠OCA) = 180° - 55° = 125°

答案 125 解析 过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE = FG = HI,
∴OM = OK = OP,
∴AO平分∠BAC,CO平分∠ACB,
∴∠OAC = $\frac{1}{2}$∠BAC,∠OCA = $\frac{1}{2}$∠BCA,
∵∠B = 70°,
∴∠BAC + ∠BCA = 180° - ∠B = 110°,
∴∠OAC + ∠OCA = $\frac{1}{2}$(∠BAC + ∠ACB) = $\frac{1}{2}$×110° = 55°,
∴∠AOC = 180° - (∠OAC + ∠OCA) = 180° - 55° = 125°

查看更多完整答案,请扫码查看


