《2025年5年中考3年模拟九年级数学下册沪科版》

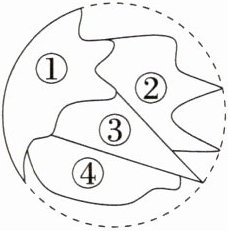
9.情境题.现实生活(2024安徽庐江四中月考,3,)小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是　　　　　　　　　　　　　　　(　　　)
　　　　　　　
A.①　　
　B.②　　
　C.③　　
　D.④

答案： A：碎片①含一段完整的弧，可在这段弧上任作两条弦，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径的长，所以带碎片①去商店可配到与原来大小一样的圆形镜子。故选A。

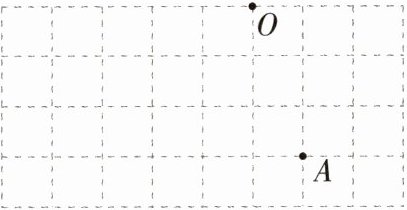
10.(2024安徽合肥十校联考,6,)如图所示的是由小正方形组成的网格,A、O在网格中小正方形的顶点处,每个小正方形的边长为1,在此网格中找两个格点(即小正方形的顶点)B、C,使O为△ABC的外心,则BC的长度可能是(M9224008)　　　　　　　　　　　　　(　　　)
　

A.3$\sqrt{2}$　
　B.2$\sqrt{5}$　　
　C.4　　　
　D.$\sqrt{17}$

答案：
B：
∵O为△ABC的外心，
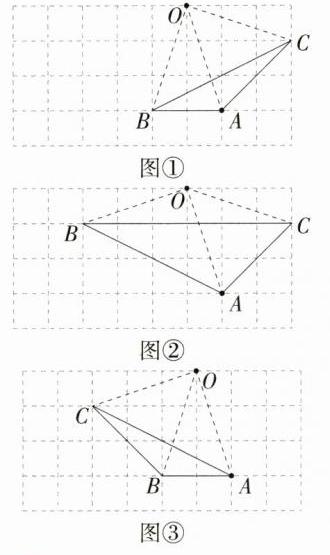
∴OA = OB = OC = $\sqrt{1^{2}+3^{2}}=\sqrt{10}$，分以下三种情况： 如图①，BC = $\sqrt{2^{2}+4^{2}} = 2\sqrt{5}$； 如图②，BC = 6； 如图③，BC = $\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$。故选B。

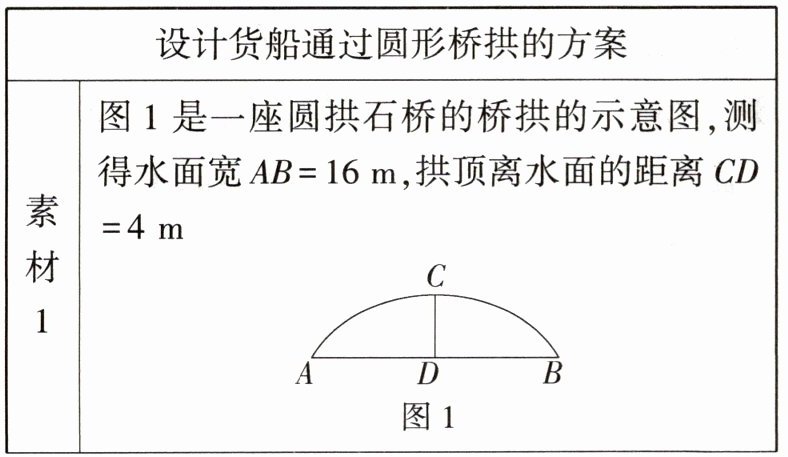
11.抽象能力)新考向.项目式学习试题(2024广西柳州城中期中)根据素材解决问题.

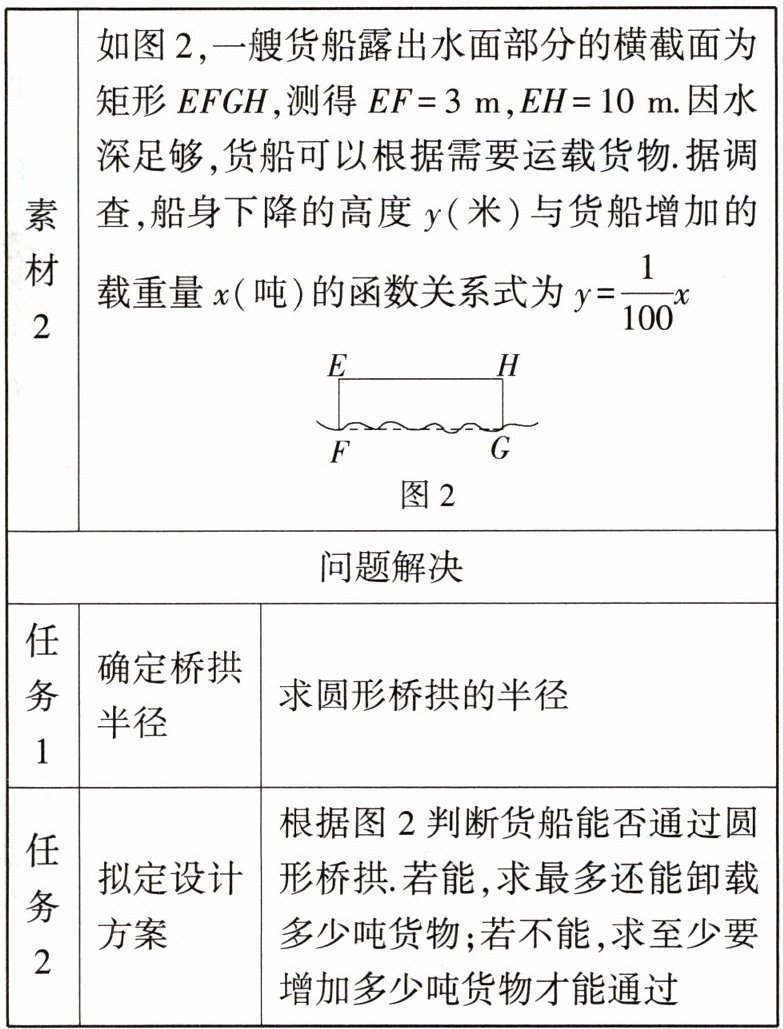
答案：
解析：任务1：设圆心为点O，连接AO，OD，易知O，D，C三点共线，如图。

设桥拱的半径为r m，则OD = (r - 4)m，
∵OC⊥AB，
∴AD = BD = $\frac{1}{2}$AB = 8 m.
∵OD² + AD² = OA²，
∴(r - 4)² + 8² = r²，
∴r = 10，
∴圆形桥拱的半径为10 m。 任务2：货船不能通过圆形桥拱，至少要增加(900 - 500$\sqrt{3}$)吨货物才能通过。 理由：当EH是⊙O的弦时，设EH与OC的交点为M，连接OE，如图，

 
∵四边形EFGH为矩形，
∴EH//FG.
∵OC⊥AB，
∴OM⊥EH，
∴EM = $\frac{1}{2}$EH = 5 m，
∴OM = $\sqrt{OE^{2}-EM^{2}} = 5\sqrt{3}$ m.
∵OC = 10 m，CD = 4 m，
∴OD = 6 m，
∴DM = (5$\sqrt{3}$ - 6)m ＜ 3 m，
∴货船不能通过圆形桥拱，
∴船露出水面部分下降的高度至少为3 - (5$\sqrt{3}$ - 6) = (9 - 5$\sqrt{3}$)m. 将y = 9 - 5$\sqrt{3}$代入y = $\frac{1}{100}$x，得x = 100×(9 - 5$\sqrt{3}$) = 900 - 500$\sqrt{3}$，
∴至少要增加(900 - 500$\sqrt{3}$)吨货物才能通过。