第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 跨语文·诗词鉴赏 用数学的方式理解“当窗理云鬓,对镜帖花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是(M9224001) ( )
A. 平移和旋转
B. 对称和旋转
C. 对称和平移
D. 旋转和平移
A. 平移和旋转
B. 对称和旋转
C. 对称和平移
D. 旋转和平移
答案:
B “当窗理云鬓,对镜帖花黄”蕴含的图形运动是对称;“坐地日行八万里”蕴含的图形运动是旋转. 故选B.
2. (2023甘肃兰州树人中学期中)如图,小明坐在秋千上,秋千旋转了76°,小明的位置也从点A运动到了点A',则旋转中心是点________,旋转角是∠________ = ________°. (M9224001)


答案:
答案:$O$;$A'OA$;$76$
解析:$\because$小明的位置绕定点$O$从点$A$运动到了点$A'$,$\therefore$旋转中心是点$O$,点$A$和点$A'$是对应点,旋转角是$\angle A'OA = 76^{\circ}$.
3. 易错题 教材变式·P11T10 在平面直角坐标系中,将抛物线y = x² + 2025绕原点按逆时针方向旋转180°,则这时抛物线对应的函数表达式为 ( )
A. y = -x² + 2025
B. y = x² - 2025
C. y = -x² - 2025
D. y = x² + 2025
A. y = -x² + 2025
B. y = x² - 2025
C. y = -x² - 2025
D. y = x² + 2025
答案:
C 抛物线$y = x^{2}+2025$开口向上,顶点位于$y$轴正半轴且距离原点$2025$个单位长度,将其绕原点按逆时针方向旋转$180^{\circ}$后,抛物线开口向下,顶点位于$y$轴负半轴且距离原点$2025$个单位长度,所以旋转后的抛物线对应的函数表达式为$y = -x^{2}-2025$,故选C.
4. (2024安徽宿州宿城一中期中)如图,把△ABC绕点A逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是(M9224001) ( )
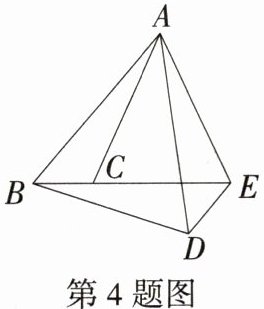
A. ∠CAE = ∠BED
B. AB = AE
C. ∠ACE = ∠ADE
D. CE = BD

A. ∠CAE = ∠BED
B. AB = AE
C. ∠ACE = ∠ADE
D. CE = BD
答案:
A 设$AD$与$BE$的交点为$O$(图略),$\because$把$\triangle ABC$以点$A$为中心逆时针旋转得到$\triangle ADE$,$\therefore \angle ABC=\angle ADE$,$\angle BAD = \angle CAE$. 又$\because \angle AOB=\angle DOE$,$\therefore \angle BED=\angle BAD=\angle CAE$. 故选A.
5. (2024安徽天长月考)如图,△AOB绕点O逆时针旋转55°得到△COD,若∠A = 100°,∠D = 50°,则∠BOC的度数是________°. (M9224001)
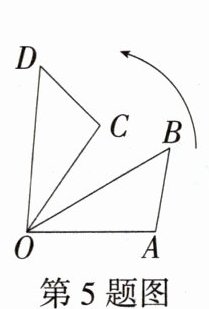

答案:
答案:$25$
解析:$\because \triangle AOB$绕点$O$逆时针旋转$55^{\circ}$得到$\triangle COD$,$\therefore \angle BOD = 55^{\circ}$,$\angle C=\angle A = 100^{\circ}$. 又$\because \angle D = 50^{\circ}$,$\therefore \angle COD = 30^{\circ}$,$\therefore \angle BOC=\angle BOD-\angle COD = 55^{\circ}-30^{\circ}=25^{\circ}$.
6. 新独家原创 如图,△ABC中,AB = AC,点P是△ABC内一点,∠BAP = 45°,将△ABP绕点A逆时针旋转后与△ACQ重合,且AQ//BC,连接PQ.若AP = 1,则PQ = ________. (M9224001)


答案:
答案:$\sqrt{2}$
解析:$\because \triangle ACQ$是由$\triangle ABP$绕点$A$逆时针旋转得到的,$\therefore \angle CAQ=\angle BAP = 45^{\circ}$. 又$AQ// BC$,$\therefore \angle ACB=\angle CAQ = 45^{\circ}$. $\because AB = AC$,$\therefore \angle ABC=\angle ACB = 45^{\circ}$,$\therefore \angle BAC = 90^{\circ}$. 由旋转的性质,得$\angle PAQ=\angle BAC = 90^{\circ}$,$AQ = AP = 1$,$\therefore PQ=\sqrt{1^{2}+1^{2}}=\sqrt{2}$.
7. (2024广西浦北期中)如图,在△ABC中,AB = BC,∠ABC = 120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°能与△ABE的边BE重合,点F是ED与AB的交点. (M9224001)
(1)求证:AE = CD.
(2)若∠DBC = 45°,求∠BFE的度数.
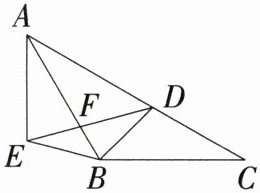
(1)求证:AE = CD.
(2)若∠DBC = 45°,求∠BFE的度数.

答案:
解析:
(1)证明:$\because$线段$BD$绕着点$B$按逆时针方向旋转$120^{\circ}$能与$\triangle ABE$的边$BE$重合,$\therefore BD = BE$,$\angle EBD = 120^{\circ}$. $\because \angle ABC = 120^{\circ}$,$\therefore \angle ABD+\angle DBC=\angle ABD+\angle ABE = 120^{\circ}$,$\therefore \angle DBC=\angle ABE$,$\because AB = BC$,$\therefore \triangle ABE\cong\triangle CBD(SAS)$,$\therefore AE = CD$.
(2)由(1)可知$\angle ABE=\angle DBC = 45^{\circ}$,$BD = BE$,$\angle EBD = 120^{\circ}$,$\therefore \angle BED=\angle BDE=\frac{1}{2}\times(180^{\circ}-120^{\circ}) = 30^{\circ}$,$\therefore \angle BFE = 180^{\circ}-\angle BED-\angle ABE = 180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$.
查看更多完整答案,请扫码查看


