第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024黑龙江牡丹江中考)下列图形既是轴对称图形,又是中心对称图形的是 ( )
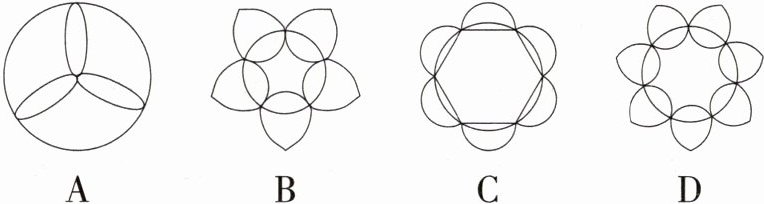
A. B. C. D.

A. B. C. D.
答案:
C:只有 C 选项中的图形绕一点旋转 180°后能与本身重合,并且至少能够找到一条直线,使得图形沿着该直线折叠,直线两旁的部分能够完全重合,即 C 中的图形既是中心对称图形,又是轴对称图形,故选 C。
2.下列语句中,是必然事件的是 ( )
A.已知∠A、∠B是锐角,则sin A = cos B
B.有一边和一角对应相等的两个三角形相似
C.抛物线y = ax²(a ≠ 0)是中心对称图形
D.垂直于弦的直径平分弦,并且平分弦所对的两条弧
A.已知∠A、∠B是锐角,则sin A = cos B
B.有一边和一角对应相等的两个三角形相似
C.抛物线y = ax²(a ≠ 0)是中心对称图形
D.垂直于弦的直径平分弦,并且平分弦所对的两条弧
答案:
D:当∠A + ∠B = 90°时,sin A = cos B,由于锐角∠A 和∠B 的和不一定是 90°,故 A 是随机事件;两边成比例且夹角相等的两个三角形相似,故 B 是随机事件;抛物线 y = ax²(a ≠ 0)是轴对称图形,不是中心对称图形,故 C 是不可能事件;由垂径定理知 D 是必然事件,故选 D。
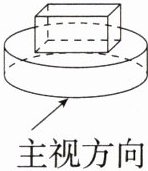
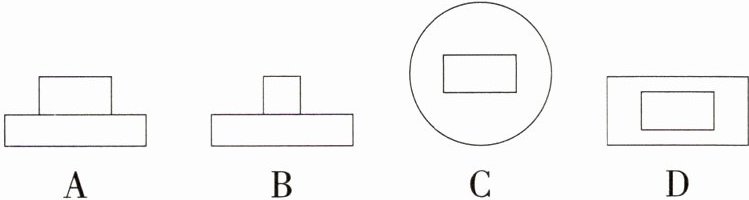
3.(2024福建中考)如图所示的是由长方体和圆柱组成的几何体,其俯视图是 ( )


答案:
C:这个几何体的俯视图是内部有一个矩形的圆,故选 C。
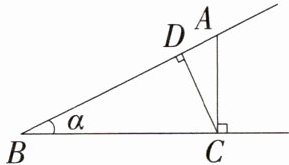
4.(2024安徽临泉期末)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cos α的值,错误的是 ( )
A.$\frac{BD}{BC}$
B.$\frac{BC}{AB}$
C.$\frac{AD}{AC}$
D.$\frac{CD}{AC}$

A.$\frac{BD}{BC}$
B.$\frac{BC}{AB}$
C.$\frac{AD}{AC}$
D.$\frac{CD}{AC}$
答案:
C:因为 AC ⊥ BC,CD ⊥ AB,所以∠α + ∠BCD = ∠ACD + ∠BCD,所以∠α = ∠ACD,所以 cos α = cos ∠ACD = $\frac{BD}{BC}=\frac{BC}{AB}=\frac{CD}{AC}$,只有选项 C 错误,符合题意,故选 C。
5.(2024安徽肥东期末)如图,C是线段AB的黄金分割点,AC>BC,则结论中正确的是 ( )

A.AC² + BC² = AB²
B.BC ≈ 0.618AB
C.AC = $\frac{\sqrt{5}-1}{2}$BC
D.BC : AC = AC : AB

A.AC² + BC² = AB²
B.BC ≈ 0.618AB
C.AC = $\frac{\sqrt{5}-1}{2}$BC
D.BC : AC = AC : AB
答案:
D:因为 C 是线段 AB 的黄金分割点,AC > BC,所以$\frac{AC}{AB}=\frac{BC}{AC}=\frac{\sqrt{5}-1}{2}\approx0.618$,所以 AC² = AB·BC,BC ≈ 0.618AC,AC = $\frac{\sqrt{5}-1}{2}AB$,只有 D 中结论正确,故选 D。
6.(2024安徽蚌埠期末)如图,AB是⊙O的直径,分别以点O和点B为圆心,大于$\frac{1}{2}$OB的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN与⊙O相交于C,D两点,若AB = 4,则CD的长为 ( )
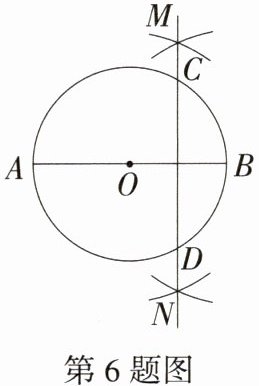
A.4$\sqrt{3}$
B.4
C.2$\sqrt{3}$
D.$\sqrt{3}$

A.4$\sqrt{3}$
B.4
C.2$\sqrt{3}$
D.$\sqrt{3}$
答案:
C:如图,连接 OC,设 AB 和 CD 交于点 P,由作图可知 CD 垂直平分 OB,因为 AB = 4,所以 OP = $\frac{1}{2}OB=\frac{1}{4}AB = 1$,OC = $\frac{1}{2}AB = 2$,所以 CP = $\sqrt{OC^{2}-OP^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,因为 CD ⊥ OB,所以 CD = 2CP = 2$\sqrt{3}$,故选 C。
C:如图,连接 OC,设 AB 和 CD 交于点 P,由作图可知 CD 垂直平分 OB,因为 AB = 4,所以 OP = $\frac{1}{2}OB=\frac{1}{4}AB = 1$,OC = $\frac{1}{2}AB = 2$,所以 CP = $\sqrt{OC^{2}-OP^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,因为 CD ⊥ OB,所以 CD = 2CP = 2$\sqrt{3}$,故选 C。

7.新独家原创 如图,已知⊙O是正方形ABCD的外接圆,F是BC的中点,AF的延长线交⊙O于点E,若AE的长是$\frac{12\sqrt{5}}{5}$,则正方形ABCD的边长是 ( )
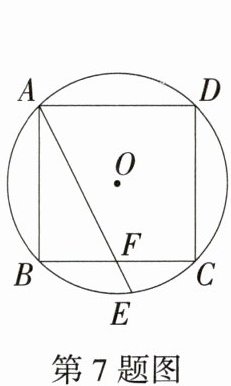
A.5
B.4
C.3
D.2

A.5
B.4
C.3
D.2
答案:
B:连接 CE(图略),因为∠AFB = ∠CFE,∠BAF = ∠ECF,所以△ABF∽△CEF,所以$\frac{AF}{CF}=\frac{BF}{EF}$。设 BF = x,则 CF = x,AB = 2x,所以 AF = $\sqrt{5}x$,EF = $\frac{12\sqrt{5}}{5}-\sqrt{5}x$,所以$\frac{\sqrt{5}x}{x}=\frac{x}{\frac{12\sqrt{5}}{5}-\sqrt{5}x}$,解得 x = 2,所以 AB = 2x = 4,故选 B。
8.一个木模(图①)的上部是圆柱,下部是底面为等边三角形的直棱柱,它的主视图和俯视图如图②所示,圆柱的底面圆是直棱柱的底面等边三角形的内切圆.若底面等边三角形的边长是2,则主视图中AB的长等于 ( )
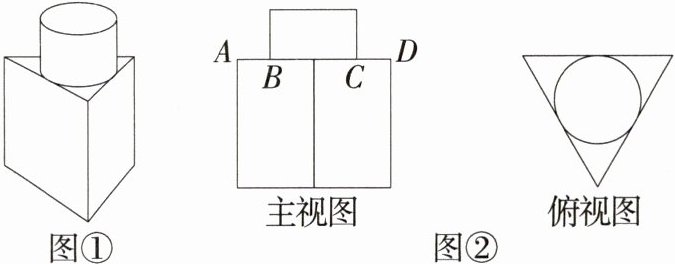
A.$\frac{2\sqrt{3}}{3}$
B.$\frac{1}{2}$
C.1 - $\frac{\sqrt{3}}{3}$
D.$\frac{2\sqrt{3}}{3}$ - 1

A.$\frac{2\sqrt{3}}{3}$
B.$\frac{1}{2}$
C.1 - $\frac{\sqrt{3}}{3}$
D.$\frac{2\sqrt{3}}{3}$ - 1
答案:
C:如图,设△EFG 的内切圆的圆心为 O,半径为 r。因为底面等边三角形的边长是 2,所以 EF = 2,连接 GO 并延长交 EF 于 H,易知 GH = $\sqrt{3}$,GH ⊥ EF,OH = r。连接 OE,OF,因为 S△EFG = S△OEG + S△OFG + S△EOF,所以$\frac{1}{2}×2×\sqrt{3}=\frac{1}{2}×(2 + 2 + 2)·r$,所以 r = $\frac{\sqrt{3}}{3}$,所以内切圆的直径 = $\frac{2\sqrt{3}}{3}$,所以主视图中 AB 的长 = $\frac{1}{2}×(2-\frac{2\sqrt{3}}{3})=1-\frac{\sqrt{3}}{3}$,故选 C。
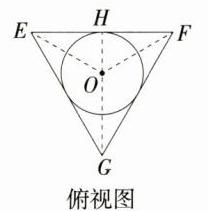
C:如图,设△EFG 的内切圆的圆心为 O,半径为 r。因为底面等边三角形的边长是 2,所以 EF = 2,连接 GO 并延长交 EF 于 H,易知 GH = $\sqrt{3}$,GH ⊥ EF,OH = r。连接 OE,OF,因为 S△EFG = S△OEG + S△OFG + S△EOF,所以$\frac{1}{2}×2×\sqrt{3}=\frac{1}{2}×(2 + 2 + 2)·r$,所以 r = $\frac{\sqrt{3}}{3}$,所以内切圆的直径 = $\frac{2\sqrt{3}}{3}$,所以主视图中 AB 的长 = $\frac{1}{2}×(2-\frac{2\sqrt{3}}{3})=1-\frac{\sqrt{3}}{3}$,故选 C。

查看更多完整答案,请扫码查看


