《2025年5年中考3年模拟九年级数学下册沪科版》

8. 情境题·现实生活 (2024安徽合肥期末改编)垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.下列垃圾分类的图标中,旋转对称图形是 ( )

答案： A 选项A中的图形绕一点旋转一定的角度$\theta(0^{\circ}＜\theta＜360^{\circ})$后能与原图形重合，是旋转对称图形. 故选A.

9. 安徽常考·网格作图题 (2024广西柳州一模)如图,在平面直角坐标系xOy中,△ABC的三个顶点分别为A(-3,4),B(-5,1),C(-1,2).
(1)若△A₁B₁C₁与△ABC关于x轴对称,请写出点A₁、B₁的坐标.
(2)画出△ABC绕原点逆时针旋转90°后的△A₂B₂C₂,并写出点C₂的坐标.

答案：
解析： （1）点$A_1$、$B_1$的坐标分别为$(-3,-4)$，$(-5,-1)$. （2）如图，$\triangle A_2B_2C_2$即为所求. 点$C_2$的坐标为$(-2,-1)$.

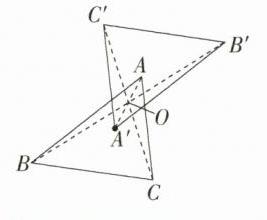
10. 如图,已知△ABC,点A'是点A以点O为旋转中心旋转180°后的对应点,试找出旋转中心O,画出△ABC绕点O旋转180°后得到的△A'B'C'.

答案：
解析：如图，连接$AA'$，取$AA'$的中点，该点即为旋转中心$O$. 连接$BO$并延长至$B'$，使$OB = OB'$，连接$CO$并延长至$C'$，使$OC = OC'$，再顺次连接点$A'$，$B'$，$C'$，则$\triangle A'B'C'$即为所求.

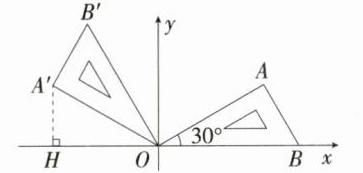
11. 新考向·代数推理 (2024河北保定月考,16,★★☆)将含有30°角的直角三角尺OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上.若OA = 4,将三角尺OAB绕原点O逆时针旋转,每秒旋转60°,则第2024秒时,点A的对应点A'的坐标为 ( )

A. (-2√3,2)
B. (-2√3,-2)
C. (2√3,-2)
D. (2√3,2)

答案：
A 根据题意可知三角尺$OAB$的位置$6$个一循环. $\because 2024 = 337\times6 + 2$，$\therefore$第$2024$秒时，直角三角尺$OAB$旋转到如图所示的位置，过点$A'$作$A'H\perp x$轴，此时$\angle A'OH = 30^{\circ}$，$OA' = OA = 4$，$\therefore A'H=\frac{1}{2}OA' = 2$，$\therefore OH=\sqrt{OA'^{2}-A'H^{2}} = 2\sqrt{3}$，$\therefore$点$A'$的坐标为$(-2\sqrt{3},2)$. 故选A.

12. (2024天津中考,11,★★☆)如图,△ABC中,∠B = 30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论一定正确的是(M9224001) ( )

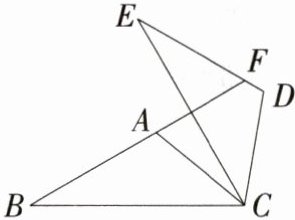
A. ∠ACB = ∠ACD
B. AC//DE
C. AB = EF
D. BF⊥CE

答案：
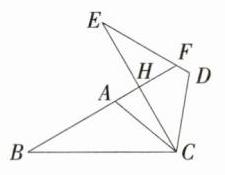
D 设$BF$与$CE$相交于一点$H$，如图. $\because$将$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，$\therefore \angle BCE=\angle ACD = 60^{\circ}$，$\because \angle B = 30^{\circ}$，$\therefore$在$\triangle BHC$中，$\angle BHC = 180^{\circ}-\angle BCE-\angle B = 90^{\circ}$，$\therefore BF\perp CE$，故D选项正确，符合题意；设$\angle ACH = x^{\circ}$，$\therefore \angle ACB = 60^{\circ}-x^{\circ}$，$\because \angle B = 30^{\circ}$，$\therefore \angle EDC=\angle BAC = 180^{\circ}-30^{\circ}-(60^{\circ}-x^{\circ}) = 90^{\circ}+x^{\circ}$，$\therefore \angle EDC+\angle ACD = 90^{\circ}+x^{\circ}+60^{\circ}=150^{\circ}+x^{\circ}$，$\because x^{\circ}$不一定等于$30^{\circ}$，$\therefore \angle EDC+\angle ACD$不一定等于$180^{\circ}$，$\therefore AC// DE$不一定成立，故B选项不正确，不符合题意；$\because \angle ACB = 60^{\circ}-x^{\circ}$，$\angle ACD = 60^{\circ}$，$x^{\circ}$不一定等于$0^{\circ}$，$\therefore \angle ACB=\angle ACD$不一定成立，故A选项不正确，不符合题意；$\because$将$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，$\therefore AB = ED = EF + FD$，$\therefore$只有当点$D$、$F$重合时，$AB = EF$，故C选项不正确，不符合题意. 故选D.

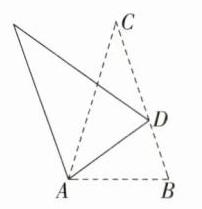
13. (2023上海中考,17,★★☆)如图,在△ABC中,∠C = 35°,将△ABC绕着点A旋转α(0° ＜ α ＜ 180°),旋转后的点B落在BC上,点B的对应点为D,连接AD,AD是∠BAC的平分线,则α = ________.

答案：
答案：$(\frac{110}{3})^{\circ}$ 解析：如图，$\because \angle BAD=\alpha$，$AD$是$\angle BAC$的平分线，$\therefore \angle CAD=\angle BAD=\alpha$. $\because \angle ADB=\angle C+\angle CAD = 35^{\circ}+\alpha$，$AB = AD$，$\therefore \angle B=\angle ADB = 35^{\circ}+\alpha$. 在$\triangle ABC$中，$\angle C+\angle CAB+\angle B = 180^{\circ}$，$\therefore 35^{\circ}+2\alpha+35^{\circ}+\alpha = 180^{\circ}$，解得$\alpha = (\frac{110}{3})^{\circ}$.