第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
22.(新考向·开放型试题)(8分)数学课上,李老师在黑板上写了如下内容:
如图,△ABC内接于⊙O,AB为⊙O的直径,AC的长为4,CD为⊙O的切线,过点O作OD⊥AB,交CD于点D,与AC交于点E.
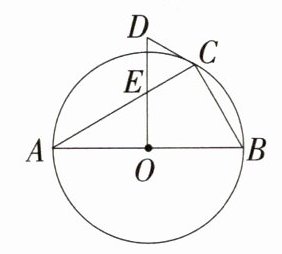
李老师要求添加条件后,编成一道题目,并解答.
(1)在黑板内容中添加条件BC = 2,求AB的长,请你解答.
(2)以下是小明和小超的对话:
小明:我添加的条件是AO = 5,这样就可以求出BC的长了.
小超:你的太简单了,我添加的条件是∠A = 30°,连接OC,就可以证明△ABC与△ODC相似.
李老师:我们这节课侧重学习的是与切线性质有关的知识,小超的证明的结论涉及了切线性质的知识,而小明的没有涉及切线性质的知识,请你解答小超提出来的问题.
如图,△ABC内接于⊙O,AB为⊙O的直径,AC的长为4,CD为⊙O的切线,过点O作OD⊥AB,交CD于点D,与AC交于点E.

李老师要求添加条件后,编成一道题目,并解答.
(1)在黑板内容中添加条件BC = 2,求AB的长,请你解答.
(2)以下是小明和小超的对话:
小明:我添加的条件是AO = 5,这样就可以求出BC的长了.
小超:你的太简单了,我添加的条件是∠A = 30°,连接OC,就可以证明△ABC与△ODC相似.
李老师:我们这节课侧重学习的是与切线性质有关的知识,小超的证明的结论涉及了切线性质的知识,而小明的没有涉及切线性质的知识,请你解答小超提出来的问题.
答案:
解析 (1)
∵AB为⊙O的直径,
∴∠ACB = 90°。
∵AC = 4,BC = 2,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。 (2)如图,连接OC。
∵∠A = 30°,
∴∠COB = 60°。
∵OD⊥AB,
∴∠DOC = 30°,
∴∠A = ∠DOC。
∵CD为⊙O的切线,
∴∠OCD = 90°,
∵AB为⊙O的直径,
∴∠ACB = 90°,
∴∠ACB = ∠OCD,
∴△ABC∽△ODC
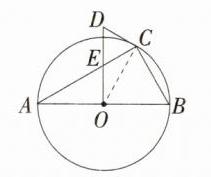
解析 (1)
∵AB为⊙O的直径,
∴∠ACB = 90°。
∵AC = 4,BC = 2,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。 (2)如图,连接OC。
∵∠A = 30°,
∴∠COB = 60°。
∵OD⊥AB,
∴∠DOC = 30°,
∴∠A = ∠DOC。
∵CD为⊙O的切线,
∴∠OCD = 90°,
∵AB为⊙O的直径,
∴∠ACB = 90°,
∴∠ACB = ∠OCD,
∴△ABC∽△ODC

23.(新考向·阅读理解试题)(2023山东济宁学院附中期末)(8分)
【阅读】
辅助线是几何解题中沟通条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
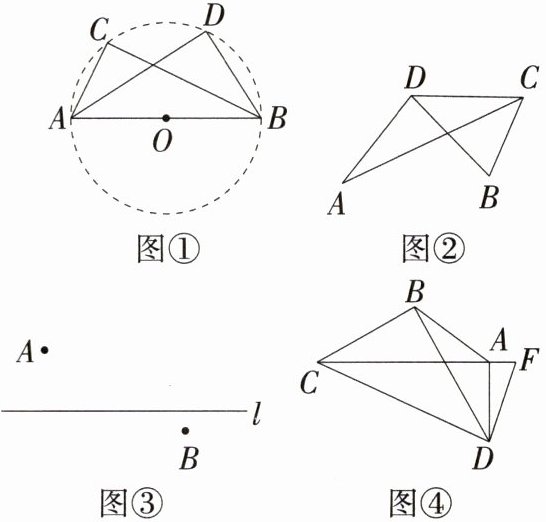
性质:如图①,若∠ACB = ∠ADB = 90°,则点D在经过A,B,C三点的圆上.
【问题解决】
运用上述材料中的信息解决以下问题:
(1)如图②,已知DA = DB = DC.求证:∠ADB = 2∠ACB.
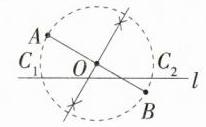
(2)如图③,点A,B位于直线l两侧.用尺规在直线l上作出点C,使得∠ACB = 90°.(保留作图痕迹,不用写法)
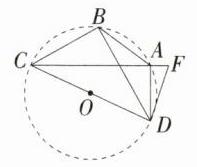
(3)如图④,在四边形ABCD中,∠CAD = 90°,CB⊥DB,点F在CA的延长线上,连接DF,∠ADF = ∠ABD.求证:DF是△ACD外接圆的切线.
【阅读】
辅助线是几何解题中沟通条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
性质:如图①,若∠ACB = ∠ADB = 90°,则点D在经过A,B,C三点的圆上.
【问题解决】
运用上述材料中的信息解决以下问题:
(1)如图②,已知DA = DB = DC.求证:∠ADB = 2∠ACB.
(2)如图③,点A,B位于直线l两侧.用尺规在直线l上作出点C,使得∠ACB = 90°.(保留作图痕迹,不用写法)
(3)如图④,在四边形ABCD中,∠CAD = 90°,CB⊥DB,点F在CA的延长线上,连接DF,∠ADF = ∠ABD.求证:DF是△ACD外接圆的切线.

答案:
解析 (1)证明:如图,由DA = DB = DC,可知点A,B,C在以D为圆心,DA长为半径的圆上,
∴∠ADB = 2∠ACB
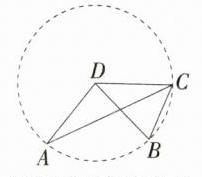
(2)如图,C₁,C₂就是要求所作的点。
(3)证明:如图,以CD的中点O为圆心,CD为直径作⊙O,则⊙O是△ACD的外接圆。 由∠DAC = ∠DBC = 90°,得点B在△ACD的外接圆上,
∴∠ACD = ∠ABD。
∵∠ADF = ∠ABD,
∴∠ACD = ∠ADF。
∵∠ACD + ∠ADC = 90°,
∴∠ADF + ∠ADC = 90°。
∴∠CDF = 90°,即CD⊥DF。
∴DF是△ACD外接圆的切线。
解析 (1)证明:如图,由DA = DB = DC,可知点A,B,C在以D为圆心,DA长为半径的圆上,
∴∠ADB = 2∠ACB

(2)如图,C₁,C₂就是要求所作的点。

(3)证明:如图,以CD的中点O为圆心,CD为直径作⊙O,则⊙O是△ACD的外接圆。 由∠DAC = ∠DBC = 90°,得点B在△ACD的外接圆上,
∴∠ACD = ∠ABD。

∵∠ADF = ∠ABD,
∴∠ACD = ∠ADF。
∵∠ACD + ∠ADC = 90°,
∴∠ADF + ∠ADC = 90°。
∴∠CDF = 90°,即CD⊥DF。
∴DF是△ACD外接圆的切线。
查看更多完整答案,请扫码查看


