第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
22.[答案含评分细则](2024广西南宁三美学校三模)(8分)美丽邕城四季常青,这与南宁市重视城市绿化密不可分,市区很多公园、广场都安装有绿地喷淋系统.现准备在某草坪上安装一个自动喷水装置,其示意图如图1,喷水装置喷射出来的水流可以近似地看成抛物线,点A、M在抛物线上,A为出水口,M为水流与地面的交点.如图2,水流距离地面的高度y(单位:m)与水流距离出水口的水平距离x(单位:m)之间具有函数关系y = -$\frac{1}{3}$(x - 1)² + $\frac{3}{4}$.
(1)自动喷水装置喷水口距离地面的高度OA = _______m.
(2)如图1,该自动喷水装置能旋转240°,它的喷灌区域是一个扇形,求它能喷灌的草坪面积(结果保留π).
(3)如图3,若喷水口正后方1米处有一条人行步道l,为保障行人安全,水流不能喷溅到步道上,请通过计算说明喷水装置安装位置是否合理.
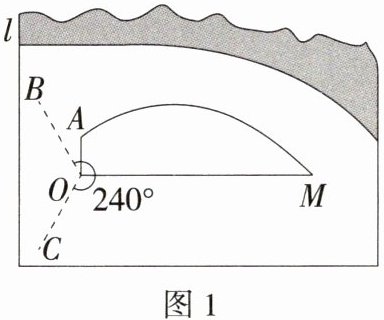
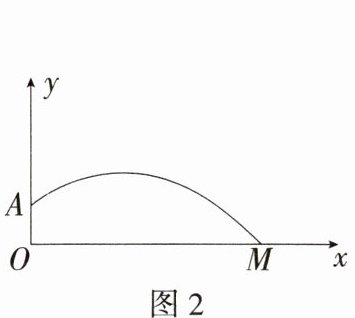
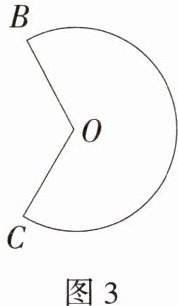
(1)自动喷水装置喷水口距离地面的高度OA = _______m.
(2)如图1,该自动喷水装置能旋转240°,它的喷灌区域是一个扇形,求它能喷灌的草坪面积(结果保留π).
(3)如图3,若喷水口正后方1米处有一条人行步道l,为保障行人安全,水流不能喷溅到步道上,请通过计算说明喷水装置安装位置是否合理.


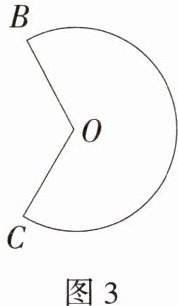
答案:
解析:
(1)$\frac{5}{12}$。
(2)当 y = 0 时,-$\frac{1}{3}(x - 1)^{2}+\frac{3}{4}=0$,解得 x = $\frac{5}{2}$或 x = -$\frac{1}{2}$(舍去),所以$\frac{240×2.5^{2}π}{360}=\frac{25}{6}π$(m²)。 答:它能喷灌的草坪面积为$\frac{25}{6}π$ m²。
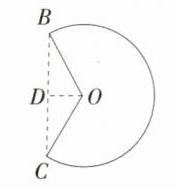
(3)如图,连接 BC,过 O 作 OD ⊥ BC 于点 D,则 BD = CD,∠BOD = ∠COD = $\frac{360° - 240°}{2}=60°$,在 Rt△OBD 中,cos∠BOD = $\frac{OD}{OB}$,所以 OD = OB·cos∠BOD = $\frac{5}{2}×\frac{1}{2}=1.25$(m)> 1 m,所以喷水装置安装位置不合理。
解析:
(1)$\frac{5}{12}$。
(2)当 y = 0 时,-$\frac{1}{3}(x - 1)^{2}+\frac{3}{4}=0$,解得 x = $\frac{5}{2}$或 x = -$\frac{1}{2}$(舍去),所以$\frac{240×2.5^{2}π}{360}=\frac{25}{6}π$(m²)。 答:它能喷灌的草坪面积为$\frac{25}{6}π$ m²。
(3)如图,连接 BC,过 O 作 OD ⊥ BC 于点 D,则 BD = CD,∠BOD = ∠COD = $\frac{360° - 240°}{2}=60°$,在 Rt△OBD 中,cos∠BOD = $\frac{OD}{OB}$,所以 OD = OB·cos∠BOD = $\frac{5}{2}×\frac{1}{2}=1.25$(m)> 1 m,所以喷水装置安装位置不合理。

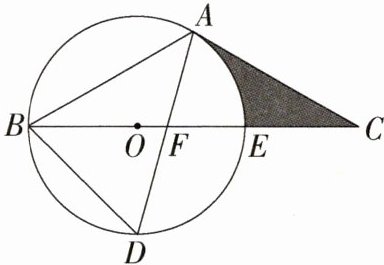
23.[答案含评分细则](10分)如图,以△ABC的BC边上一点O为圆心的圆经过A、B两点,且与BC边交于点E,D为$\overset{\frown}{BDE}$的中点,连接AD交BC于点F,若AC = FC.
(1)求证:AC是⊙O的切线.
(2)若BF = 8,DF = 2$\sqrt{10}$,求⊙O的半径.
(3)若∠ADB = 60°,BD = 1,求阴影部分的面积.(结果保留π)
(1)求证:AC是⊙O的切线.
(2)若BF = 8,DF = 2$\sqrt{10}$,求⊙O的半径.
(3)若∠ADB = 60°,BD = 1,求阴影部分的面积.(结果保留π)

答案:
解析:
(1)证明:连接 OA、OD,如图, 因为 D 为$\overset{\frown}{BDE}$的中点,所以 OD ⊥ BE,所以∠ODF + ∠OFD = 90°。 因为 CA = CF,所以∠CAF = ∠CFA。又∠CFA = ∠OFD,所以∠OFD = ∠CAF。所以∠ODF + ∠CAF = 90°。 因为 OA = OD,所以∠ODA = ∠OAD,所以∠OAD + ∠CAF = 90°,即∠OAC = 90°,所以 OA ⊥ AC,又 OA 是半径,所以 AC 是⊙O 的切线。
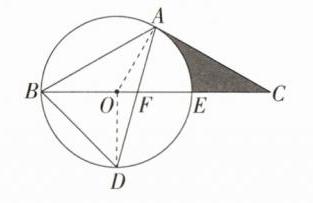
(2)设⊙O 的半径为 r,则 OF = 8 - r,在 Rt△ODF 中,DF = 2$\sqrt{10}$,所以(8 - r)² + r² = (2$\sqrt{10}$)²,解得 r₁ = 6,r₂ = 2(舍去),所以⊙O 的半径为 6。
(3)因为∠BOD = 90°,OB = OD,所以△BOD 为等腰直角三角形,因为 BD = 1,所以 OB = $\frac{\sqrt{2}}{2}BD=\frac{\sqrt{2}}{2}$,所以 OA = $\frac{\sqrt{2}}{2}$,因为∠ADB = 60°,所以∠AOB = 2∠ADB = 120°,所以∠AOE = 60°,在 Rt△OAC 中,AC = $\sqrt{3}OA=\frac{\sqrt{6}}{2}$,所以阴影部分的面积 = $\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{6}}{2}-\frac{60·π·(\frac{\sqrt{2}}{2})^{2}}{360}=\frac{3\sqrt{3}-π}{12}$。
解析:
(1)证明:连接 OA、OD,如图, 因为 D 为$\overset{\frown}{BDE}$的中点,所以 OD ⊥ BE,所以∠ODF + ∠OFD = 90°。 因为 CA = CF,所以∠CAF = ∠CFA。又∠CFA = ∠OFD,所以∠OFD = ∠CAF。所以∠ODF + ∠CAF = 90°。 因为 OA = OD,所以∠ODA = ∠OAD,所以∠OAD + ∠CAF = 90°,即∠OAC = 90°,所以 OA ⊥ AC,又 OA 是半径,所以 AC 是⊙O 的切线。

(2)设⊙O 的半径为 r,则 OF = 8 - r,在 Rt△ODF 中,DF = 2$\sqrt{10}$,所以(8 - r)² + r² = (2$\sqrt{10}$)²,解得 r₁ = 6,r₂ = 2(舍去),所以⊙O 的半径为 6。
(3)因为∠BOD = 90°,OB = OD,所以△BOD 为等腰直角三角形,因为 BD = 1,所以 OB = $\frac{\sqrt{2}}{2}BD=\frac{\sqrt{2}}{2}$,所以 OA = $\frac{\sqrt{2}}{2}$,因为∠ADB = 60°,所以∠AOB = 2∠ADB = 120°,所以∠AOE = 60°,在 Rt△OAC 中,AC = $\sqrt{3}OA=\frac{\sqrt{6}}{2}$,所以阴影部分的面积 = $\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{6}}{2}-\frac{60·π·(\frac{\sqrt{2}}{2})^{2}}{360}=\frac{3\sqrt{3}-π}{12}$。
查看更多完整答案,请扫码查看


