《2025年5年中考3年模拟九年级数学下册沪科版》

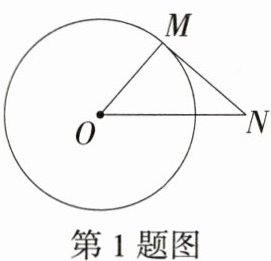
1.(2024安徽合肥包河期末)如图，MN是⊙O的切线，M是切点，连接OM、ON.若∠N = 36°，则∠MON的度数为 ( )

A.44°
B.64°
C.36°
D.54°

答案： D：因为MN是⊙O的切线，M是切点，所以半径OM⊥MN，即∠OMN = 90°。又因为∠N = 36°，所以∠MON = 90° - ∠N = 54°，故选D。

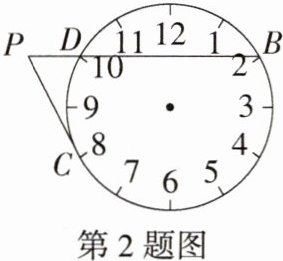
2.[新考法](2023河北衡水桃城中学期末)如图所示的是一个钟表表盘，连接整点2时与整点10时的B、D两点并延长，交过整点8时的C点的切线于点P，若PC = 2，则表盘的半径长为(M9224009) ( )

A.3
B.$\sqrt{3}$
C.2$\sqrt{3}$
D.3$\sqrt{3}$

答案：
B：本题利用钟表考查切线的性质。设钟表表盘的中心为点O，连接BC，OD，由题意得点O在BC上，易知∠DOC = 2×30° = 60°，所以∠DBC = $\frac{1}{2}$∠DOC = 30°。因为PC与⊙O相切于点C，所以∠BCP = 90°，则BC = $\frac{CP}{\tan30^{\circ}}=\frac{2}{\frac{\sqrt{3}}{3}} = 2\sqrt{3}$，所以表盘的半径长为$\sqrt{3}$，故选B。

3.[易错题](2023浙江宁波期末)点P为⊙O外一点，直线PO与⊙O的两个公共点为A、B，过点P作⊙O的切线，点C为切点，连接AC.若∠CPO = 50°，则∠CAB的度数为________.

答案：
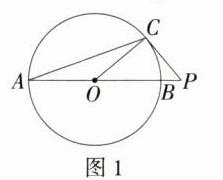
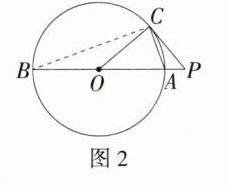
答案：20°或70° 解析：如图1，因为PC是⊙O的切线，C为切点，所以OC⊥PC，即∠OCP = 90°。因为∠CPO = 50°，所以∠COP = 40°。又因为OC = OA，所以∠CAB = ∠ACO = $\frac{1}{2}$∠COP = 20°。 如图2，连接BC，易知∠CBA = 20°，因为AB是⊙O的直径，所以∠ACB = 90°，所以∠CAB = 70°。综上，∠CAB的度数为20°或70°。

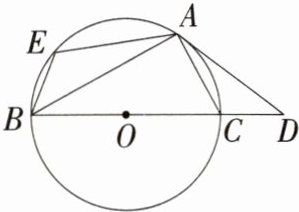
4.(2024安徽太和期末)如图，BC是⊙O的直径，点A在⊙O上，AD与⊙O相切于点A，交BC的延长线于点D，E是$\overset{\frown}{AB}$上一点，连接AB，AC，AE，BE.(M9224009)
(1)若∠AEB = 110°，求∠D的度数.
(2)求证：∠CAD = ∠ABC.

答案：
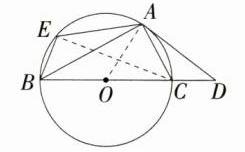
解析： （1）连接CE，OA，如图。因为BC是⊙O的直径，所以∠BEC = 90°。因为∠AEB = 110°，所以∠AEC = 110° - 90° = 20°，所以∠AOD = 2∠AEC = 40°。因为AD与⊙O相切于A，所以OA⊥AD，即∠OAD = 90°，所以∠D = 90° - ∠AOD = 50°。 （2）证明：因为BC是⊙O的直径，所以∠BAC = 90°，又∠OAD = 90°，所以∠BAO + ∠OAC = ∠CAD + ∠OAC = 90°，所以∠CAD = ∠BAO，因为OA = OB，所以∠BAO = ∠ABC，所以∠CAD = ∠ABC。

5.(2023河北晋州期末)如图所示，△POM中，点M在⊙O上，点P在⊙O外，OP交⊙O于点N，以下条件不能判定PM是⊙O的切线的是 (M9224009) ( )

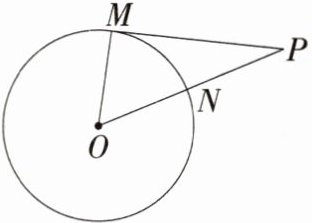
A.∠O + ∠P = 90°
B.∠O + ∠P = ∠OMP
C.OM² + PM² = OP²
D.点N是OP的中点

答案： D：由∠O + ∠P = 90°，∠O + ∠P = ∠OMP，OM² + PM² = OP²都可以得到∠OMP = 90°，进而证出PM是⊙O的切线。由点N是OP的中点，不能得到∠OMP = 90°，不能说明PM是⊙O的切线，故选D。

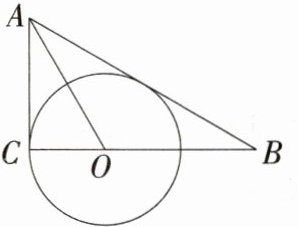
6.[新独家原创]如图，在Rt△ABC中，∠ACB = 90°，O是BC边上的一点，以O点为圆心，OC为半径作⊙O，若要判定AB是⊙O的切线，则可以补充的一个条件是__________.

答案： 答案：AO平分∠BAC（答案不唯一） 解析：添加AO平分∠BAC，作OD⊥AB于点D，由∠ACO = 90°，易知OD = OC，所以AB是⊙O的切线。

7.[新考向·尺规作图 一题多解](2024陕西西安高新一中一模)如图，已知P是⊙O外一点.请利用尺规过点P作⊙O的一条切线.
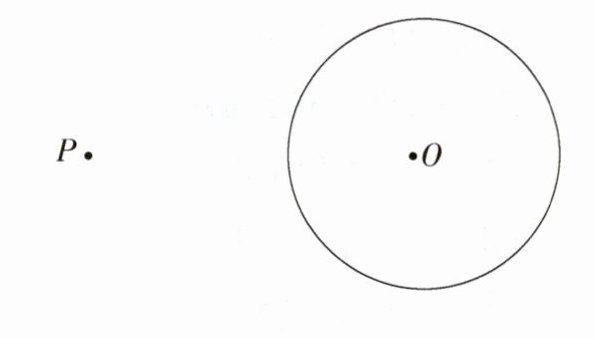
(保留作图的痕迹，写出必要的文字说明). (M9224010)

答案：
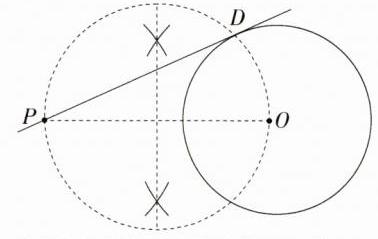
解析： 【解法一】如图，连接OP，以OP为直径作圆交⊙O于D，作直线PD，直线PD即为所求。

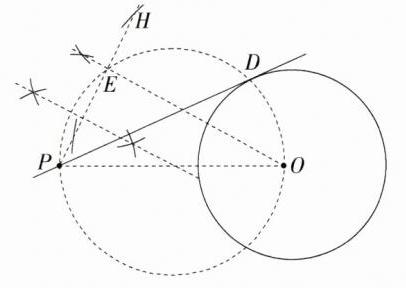
【解法二】如图，连接OP，作射线PH，作OE⊥PH于E，作△POE的外接圆交⊙O于D，作直线PD，直线PD即为所求。