《2025年5年中考3年模拟九年级数学下册沪科版》

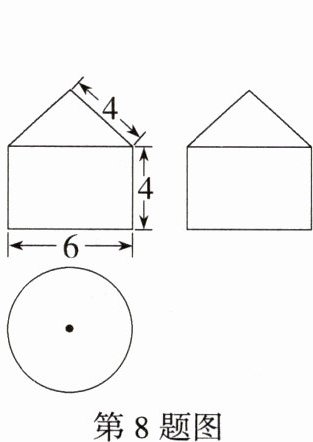
8.(2023山东济宁中考,8,★★☆)一个几何体的三视图如图，则这个几何体的表面积是 ( )

A.39π
B.45π
C.48π
D.54π

答案： 答案：B 解析：由三视图可知，该几何体是由一个圆锥和一个圆柱组成的，其中圆柱底面圆的直径为6，高为4，圆锥底面圆的直径为6，母线长为4，所以该几何体的表面积为π×$(\frac{6}{2})^{2}$ + 6π×4 + $\frac{1}{2}$×6π×4 = 45π，故选B。

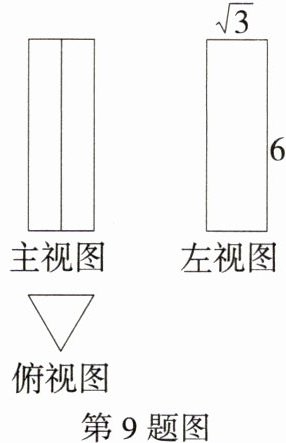
9.(2024重庆南岸期末,15,★★☆)如图所示的是一个几何体的三视图，其中俯视图为正三角形，则该几何体的侧面积为_______.

答案： 答案：36 解析：由三视图知该几何体是一个三棱柱，且该三棱柱的高为6，底面是一个高为$\sqrt{3}$的正三角形，易知该三棱柱的底面正三角形的边长为2，
∴该几何体的侧面积是(2 + 2 + 2)×6 = 36， 故答案为36。

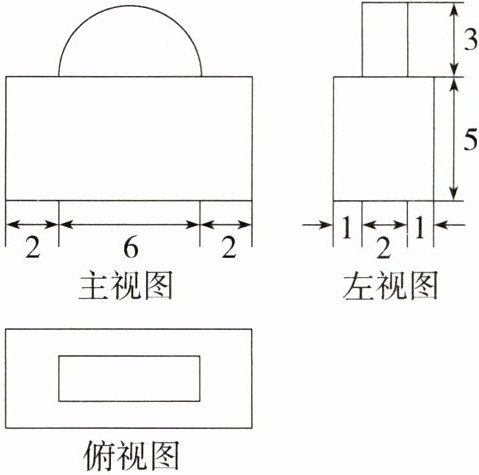
10.(2022安徽滁州定远育才实验学校月考,17,★★☆)一个几何体的三视图如图所示，求该几何体的体积.

答案： 解析：根据三视图可知该几何体由一个长方体和一个半圆柱组成，长方体的长、宽、高分别为10、4、5，半圆柱的高为2，底面半圆的半径为3，
∴长方体的体积为10×4×5 = 200， 半圆柱的体积为$\frac{1}{2}$×π×$3^{2}$×2 = 9π，
∴该几何体的体积为200 + 9π。

11.空间观念 如图，一透明的敞口正方体容器ABCD - A'B'C'D'中装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α(∠CBE = α).(M9225004)
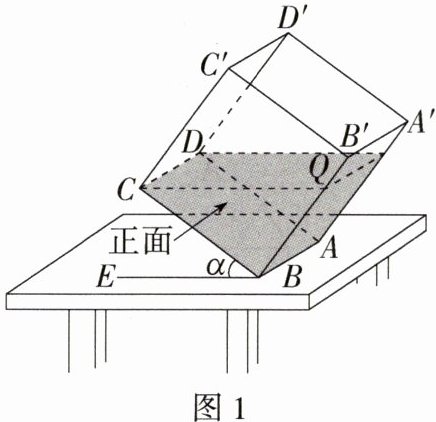
探究：如图1，液面刚好过棱CD，并与棱BB'交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示.
解决问题：
(1)CQ与BE的位置关系是_______，BQ的长是_______dm.
(2)求液体的体积(提示：V液 = S△BCQ×高AB).
(3)求液面到桌面的高度和倾斜角α的度数(sin 37°≈$\frac{3}{5}$，tan 37°≈$\frac{3}{4}$).

答案： 解析： （1）平行；3。 （2）$V_{液}$ = $\frac{1}{2}$×3×4×4 = 24（$dm^{3}$）。 （3）过点B作BF⊥CQ，垂足为F（图略）。
∵$S_{\triangle BCQ}$ = $\frac{1}{2}$×3×4 = $\frac{1}{2}$×5×BF，
∴BF = $\frac{12}{5}$ dm，
∴液面到桌面的高度是$\frac{12}{5}$ dm。 由（1）可知CQ//BE，
∴α = ∠BCQ。
∵在Rt△BCQ中，tan∠BCQ = $\frac{BQ}{BC}$ = $\frac{3}{4}$，
∴α = ∠BCQ≈37°。