第94页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
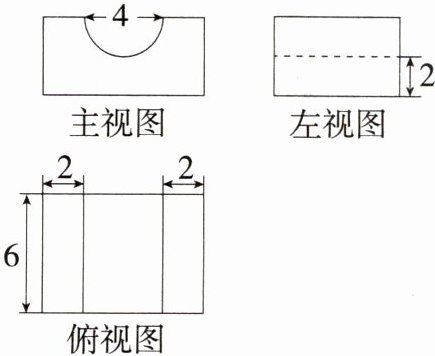
16.[答案含评分细则](2024山东烟台福山期末)(6分)某几何体的三视图如图所示,其中主视图中半圆的半径为2.请求出该几何体的体积V和表面积S.

答案:
解析:由三视图可知,该几何体是一个长、宽、高分别为 8、6、4 的长方体中挖去一个直径为 4 的半圆柱,
S = 6×4×2 + 6×8 + 6×2×2 + (8×4-$\frac{1}{2}π×2^{2}$)×2 + π×4×$\frac{1}{2}×6 = 48 + 48 + 24 + 64 - 4π + 12π = 184 + 8π$,
V = 8×6×4-$\frac{1}{2}π×2^{2}×6 = 192 - 12π$。
17.[答案含评分细则]安徽常考·网格作图题(2024安徽安庆四中二模)(6分)如图,在平面直角坐标系中,网格的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点分别为A(1,2),B(3,1),C(2,3),先以原点O为位似中心在第三象限内画一个△A₁B₁C₁,使它与△ABC位似,且相似比为2 : 1,然后再把△ABC绕原点O逆时针旋转90°得到△A₂B₂C₂.
(1)画出△A₁B₁C₁.
(2)画出△A₂B₂C₂.
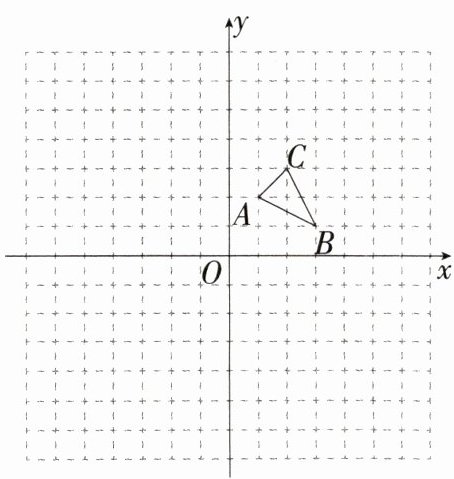
(1)画出△A₁B₁C₁.
(2)画出△A₂B₂C₂.

答案:
解析:
(1)如图,△A₁B₁C₁ 即为所作。
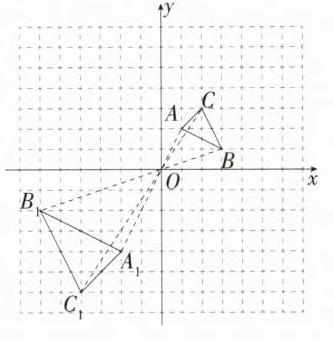
(2)如图,△A₂B₂C₂ 即为所作。
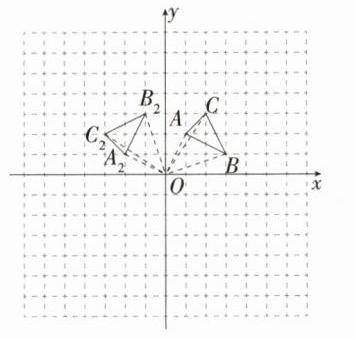
解析:
(1)如图,△A₁B₁C₁ 即为所作。

(2)如图,△A₂B₂C₂ 即为所作。

18.[答案含评分细则](2024安徽合肥包河期末)(6分)如图,一次函数y = kx + b的图象交y轴于点C(0,2),与反比例函数y = $\frac{m}{x}$的图象交于A,B两点,且A点坐标为(-3,-1).
(1)确定上述反比例函数和一次函数的表达式.
(2)直接写出不等式kx + b < $\frac{m}{x}$的解集.
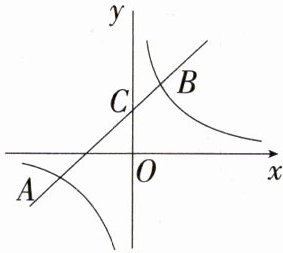
(1)确定上述反比例函数和一次函数的表达式.
(2)直接写出不等式kx + b < $\frac{m}{x}$的解集.

答案:
解析:
(1)因为 A(-3,-1)在反比例函数 y = $\frac{m}{x}$的图象上,所以 m = 3,所以 y = $\frac{3}{x}$。 因为 A(-3,-1),C(0,2)在直线 y = kx + b 上,所以$\begin{cases}-3k + b = -1\\b = 2\end{cases}$,解得$\begin{cases}k = 1\\b = 2\end{cases}$,所以 y = x + 2。
(2)x < -3 或 0 < x < 1。
(1)因为 A(-3,-1)在反比例函数 y = $\frac{m}{x}$的图象上,所以 m = 3,所以 y = $\frac{3}{x}$。 因为 A(-3,-1),C(0,2)在直线 y = kx + b 上,所以$\begin{cases}-3k + b = -1\\b = 2\end{cases}$,解得$\begin{cases}k = 1\\b = 2\end{cases}$,所以 y = x + 2。
(2)x < -3 或 0 < x < 1。
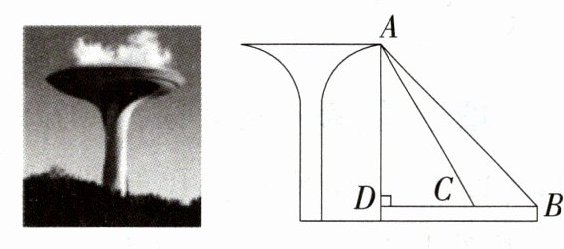
19.[答案含评分细则](2024安徽无为三模)(7分)合肥园博园由原骆岗机场改建而成,原机场信号塔改建成了七彩蘑菇塔.在综合实践活动课中,某小组的同学决定利用测角仪测量这座七彩蘑菇塔的高度(测角仪高度为1米).他们的操作方法如下:如图,在B处测得塔顶A的仰角为45°,然后向塔基方向直行22.5米到达C处,此时测得塔顶A的仰角为58°.请帮助他们计算出塔的高度.(参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)

答案:
解析:由题意得 BC = 22.5 米,AD ⊥ DB,设 DC = x 米,则 BD = BC + DC = (22.5 + x)米,
在 Rt△ACD 中,∠ACD = 58°,所以 AD = CD·tan 58°≈1.6x(米),
在 Rt△ABD 中,∠ABD = 45°,所以 AD = BD = (22.5 + x)米,
所以 1.6x = 22.5 + x,解得 x = 37.5,所以 AD = 22.5 + 37.5 = 60(米),
因为测角仪的高度为 1 米,所以塔的高度为 61 米。
答:塔的高度为 61 米。
查看更多完整答案,请扫码查看


