第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
7.(2024安徽宿州宿城一中期末,5,★☆☆)物体正投影的形状、大小与它相对于投影面的位置有关.一个正方形纸板的正投影不可能是( )
A.一条线段
B.一个与原正方形全等的正方形
C.一个邻边不等的平行四边形
D.一个等腰梯形
A.一条线段
B.一个与原正方形全等的正方形
C.一个邻边不等的平行四边形
D.一个等腰梯形
答案:
D:当正方形纸板所在平面与光线平行时,得到的正投影是一条线段;当正方形纸板所在平面与光线垂直时,得到一个与该正方形纸板大小一样的正方形;当正方形纸板所在平面与光线不垂直也不平行时,得到一个平行四边形(邻边可以不等)。正方形纸板的正投影不可能是等腰梯形。故选D。
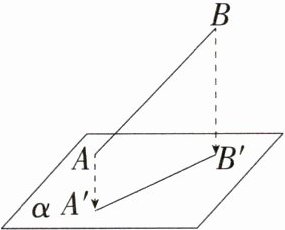
8.(2024山东莱西期中,15,★☆☆)如图,一条线段AB在平面α内的正投影为A'B',AB = 2$\sqrt{2}$,A'B' = $\sqrt{6}$,则∠B的度数为________.

答案:
答案:$60^{\circ}$ 解析:如图,过$A$作$AC\perp BB'$,交$BB'$于$C$点。 $\because AB$在平面$\alpha$内的正投影为$A'B'$, $\therefore\angle AA'B'=\angle BB'A' = 90^{\circ}$, $\therefore$四边形$AA'B'C$是矩形,$\therefore AC = A'B'=\sqrt{6}$, $\therefore\sin B=\frac{AC}{AB}=\frac{\sqrt{6}}{2\sqrt{2}}=\frac{\sqrt{3}}{2}$,$\therefore\angle B = 60^{\circ}$。
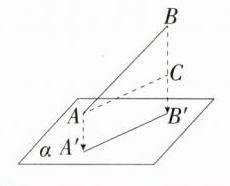
答案:$60^{\circ}$ 解析:如图,过$A$作$AC\perp BB'$,交$BB'$于$C$点。 $\because AB$在平面$\alpha$内的正投影为$A'B'$, $\therefore\angle AA'B'=\angle BB'A' = 90^{\circ}$, $\therefore$四边形$AA'B'C$是矩形,$\therefore AC = A'B'=\sqrt{6}$, $\therefore\sin B=\frac{AC}{AB}=\frac{\sqrt{6}}{2\sqrt{2}}=\frac{\sqrt{3}}{2}$,$\therefore\angle B = 60^{\circ}$。

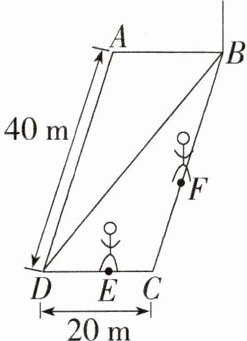
9.应用意识 (2024福建泉州期末)甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为( )
A.4 m
B.8 m
C.12 m
D.16 m

A.4 m
B.8 m
C.12 m
D.16 m
答案:
B:连接$EF$,如图, 由题可知$EF// BD$,$\therefore\triangle CEF\sim\triangle CDB$, $\therefore\frac{CE}{CD}=\frac{CF}{CB}$, $\because$两人同时从点$B$出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍, $\therefore BC + CE = 2BF = 40 + CE$,$\therefore BF=\frac{1}{2}(40 + CE)=20+\frac{1}{2}CE$,$\therefore CF = 40 - 20-\frac{1}{2}CE = 20-\frac{1}{2}CE$,$\therefore\frac{CE}{20}=\frac{20-\frac{1}{2}CE}{40}$,$\therefore CE = 8\text{ m}$,故选B。
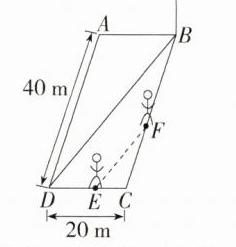
B:连接$EF$,如图, 由题可知$EF// BD$,$\therefore\triangle CEF\sim\triangle CDB$, $\therefore\frac{CE}{CD}=\frac{CF}{CB}$, $\because$两人同时从点$B$出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍, $\therefore BC + CE = 2BF = 40 + CE$,$\therefore BF=\frac{1}{2}(40 + CE)=20+\frac{1}{2}CE$,$\therefore CF = 40 - 20-\frac{1}{2}CE = 20-\frac{1}{2}CE$,$\therefore\frac{CE}{20}=\frac{20-\frac{1}{2}CE}{40}$,$\therefore CE = 8\text{ m}$,故选B。

10.创新意识 学习投影后,小明、小颖利用灯光下自己影子的长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB = 4.5 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
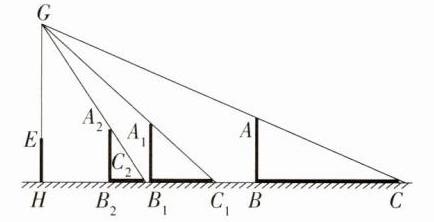
(3)如果小明沿线段BH向小颖走去,当小明走到BH的中点B₁处时,其影子为B₁C₁;当小明继续走剩下路程的$\frac{1}{3}$到B₂处时,其影子为B₂C₂;当小明继续走剩下路程的$\frac{1}{4}$到B₃处时,其影子为B₃C₃;…….按此规律继续走下去,当小明走剩下路程的$\frac{1}{n + 1}$到Bₙ处时,其影子BₙCₙ的长为________m.(用含n的代数式表示)
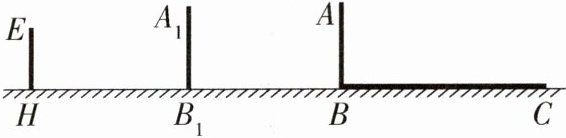
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
(3)如果小明沿线段BH向小颖走去,当小明走到BH的中点B₁处时,其影子为B₁C₁;当小明继续走剩下路程的$\frac{1}{3}$到B₂处时,其影子为B₂C₂;当小明继续走剩下路程的$\frac{1}{4}$到B₃处时,其影子为B₃C₃;…….按此规律继续走下去,当小明走剩下路程的$\frac{1}{n + 1}$到Bₙ处时,其影子BₙCₙ的长为________m.(用含n的代数式表示)

答案:
解析:
(1)如图所示。
(2)根据题意,得$\triangle ABC\sim\triangle GHC$,$\therefore\frac{AB}{GH}=\frac{BC}{HC}$, $\therefore\frac{1.6}{GH}=\frac{3}{4.5 + 3}$,$\therefore GH = 4\text{ m}$。 答:路灯灯泡的垂直高度$GH$是4 m。
(3)$\frac{3}{n + 1}$。 详解:如图,易知$\triangle A_1B_1C_1\sim\triangle GHC_1$, $\therefore\frac{A_1B_1}{GH}=\frac{B_1C_1}{HC_1}$,即$\frac{1.6}{4}=\frac{B_1C_1}{B_1C_1 + 2.25}$,$\therefore B_1C_1 = 1.5\text{ m}$。 同理$\frac{A_2B_2}{GH}=\frac{B_2C_2}{HC_2}$,即$\frac{1.6}{4}=\frac{B_2C_2}{B_2C_2 + 1.5}$,$\therefore B_2C_2 = 1\text{ m}$, $\therefore\frac{1.6}{4}=\frac{B_nC_n}{B_nC_n+\frac{1}{n + 1}\times4.5}$,$\therefore B_nC_n=\frac{3}{n + 1}\text{ m}$。
解析:
(1)如图所示。
(2)根据题意,得$\triangle ABC\sim\triangle GHC$,$\therefore\frac{AB}{GH}=\frac{BC}{HC}$, $\therefore\frac{1.6}{GH}=\frac{3}{4.5 + 3}$,$\therefore GH = 4\text{ m}$。 答:路灯灯泡的垂直高度$GH$是4 m。
(3)$\frac{3}{n + 1}$。 详解:如图,易知$\triangle A_1B_1C_1\sim\triangle GHC_1$, $\therefore\frac{A_1B_1}{GH}=\frac{B_1C_1}{HC_1}$,即$\frac{1.6}{4}=\frac{B_1C_1}{B_1C_1 + 2.25}$,$\therefore B_1C_1 = 1.5\text{ m}$。 同理$\frac{A_2B_2}{GH}=\frac{B_2C_2}{HC_2}$,即$\frac{1.6}{4}=\frac{B_2C_2}{B_2C_2 + 1.5}$,$\therefore B_2C_2 = 1\text{ m}$, $\therefore\frac{1.6}{4}=\frac{B_nC_n}{B_nC_n+\frac{1}{n + 1}\times4.5}$,$\therefore B_nC_n=\frac{3}{n + 1}\text{ m}$。

查看更多完整答案,请扫码查看


