《2025年5年中考3年模拟九年级数学下册沪科版》

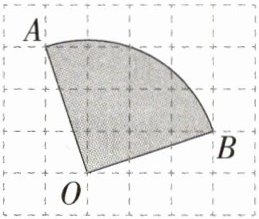
8.（2022江苏苏州中考）如图，在由小正方形组成的5×6的长方形网格飞镖游戏板中，每块小正方形除颜色外都相同，小正方形的顶点称为格点，扇形AOB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的（击中扇形的边界或没有击中游戏板，则重投1次），任意投掷飞镖1次，飞镖击中扇形AOB（阴影部分）的概率是（ ）

A.$\frac{\pi}{12}$
B.$\frac{\pi}{24}$
C.$\frac{\sqrt{10}\pi}{60}$
D.$\frac{\sqrt{5}\pi}{60}$

答案： A.设每块小正方形的边长均为1，由题图可知，飞镖游戏板总面积为5×6 = 30，OB = $\sqrt{3^{2}+1^{2}}=\sqrt{10}$，
∴阴影部分面积为$\frac{90\cdot\pi\times(\sqrt{10})^{2}}{360}=\frac{5\pi}{2}$，
∴飞镖击中扇形AOB（阴影部分）的概率是$\frac{\frac{5\pi}{2}}{30}=\frac{\pi}{12}$，故选A。

9.地中海贫血症（简称“地贫”）是一种隐性遗传病，我国长江以南为高发区.若夫妇双方均为地贫基因携带者，则子代的遗传概率情况：$\frac{1}{2}$为轻型地贫，$\frac{1}{4}$为健康，$\frac{1}{4}$为重型地贫.若夫（XY）妇（XX）双方均为地贫基因携带者，则他们生一个健康女孩的概率是（ ）
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{3}{8}$
D.$\frac{1}{8}$

答案： D.性别遗传情况如下表： | | X | Y | | ---- | ---- | ---- | | X | XX | XY | | X | XX | XY | 从性别遗传情况可知，夫妇生一个女孩的概率是$\frac{2}{4}=\frac{1}{2}$。已知夫妇双方均为地贫基因携带者，子代健康的概率为$\frac{1}{4}$，则他们生一个健康女孩的概率是$\frac{1}{2}\times\frac{1}{4}=\frac{1}{8}$。故选D。

10.2024年元旦期间，某超市为了增加销售额，举办了“购物抽奖”活动：凡购物达到200元即可抽奖1次，达到400元可抽奖2次，……，依此类推.抽奖方式：在不透明的箱子中有四个相同的小球，四个小球上分别写有对应奖品的价值为10元、15元、20元和“谢谢惠顾”的字样，抽奖1次，随机从四个小球抽取一个；抽奖2次时，记录第1次抽奖的结果后放回箱子中摇匀再进行第2次抽取，…….小明和妈妈一共购买了420元的物品，则小明和妈妈获得奖品总价值不低于30元的概率为（ ）
A.$\frac{1}{6}$
B.$\frac{1}{4}$
C.$\frac{3}{8}$
D.$\frac{1}{2}$

答案： C.因为小明和妈妈一共购买了420元的物品，所以他们获得了两次抽奖的机会，两次抽奖获得奖品总价值的情况如下： | | 10 | 15 | 20 | 谢谢惠顾 | | ---- | ---- | ---- | ---- | ---- | | 10 | 20 | 25 | 30 | 10 | | 15 | 25 | 30 | 35 | 15 | | 20 | 30 | 35 | 40 | 20 | | 谢谢惠顾 | 10 | 15 | 20 | 0 | 由表格可得，共有16种等可能出现的结果，其中小明和妈妈获得奖品总价值不低于30元的情况有6种，
∴小明和妈妈获得奖品总价值不低于30元的概率 = $\frac{6}{16}=\frac{3}{8}$，故选C。

11.跨化学·燃烧 （2023广东惠州惠东期末）“氢气在氧气中燃烧生成水”，这是________事件.（填“随机”“不可能”或“必然”）

答案： 必然 **解析** “氢气在氧气中燃烧生成水”一定会发生，这是必然事件。

12.（2024江苏盐城盐都三模）事件A发生的概率为$\frac{1}{20}$，大量重复做这种试验，估计事件A平均每100次发生的次数是________.

答案： 5 **解析** 事件A发生的概率为$\frac{1}{20}$，大量重复做这种试验，估计事件A平均每100次发生的次数为100×$\frac{1}{20}$ = 5。

13.新考法 （2023安徽蚌埠禹会模拟）已知一包糖果共有5种颜色（糖果只有颜色差别），如图所示的是各颜色糖果所占百分比的统计图，则在这包糖果中任意取一粒，取出糖果的颜色为绿色或棕色的概率是________.

答案： $\frac{1}{2}$ **解析** 本题通过扇形统计图知识考查概率，题目新颖。棕色所占的百分比为1 - 20% - 15% - 30% - 15% = 1 - 80% = 20%，所以P（取出糖果的颜色为绿色或棕色） = 30% + 20% = 50% = $\frac{1}{2}$。

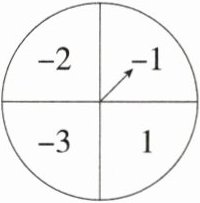
14.（2024河南三门峡二模）如图所示的是数学活动课上制作的一个转盘，盘面被分成四个相等的扇形区域，并分别标有数-3，-2，-1，1.若转动转盘两次，每次转盘停止后指针所指区域的数分别记为m，n（指针恰好在分界线上时，需重新转动转盘），则直线y = mx + n不经过第四象限的概率是__________.

答案： $\frac{1}{16}$ **解析** 列表如下： | | -3 | -2 | -1 | 1 | | ---- | ---- | ---- | ---- | ---- | | -3 | (-3,-3) | (-3,-2) | (-3,-1) | (-3,1) | | -2 | (-2,-3) | (-2,-2) | (-2,-1) | (-2,1) | | -1 | (-1,-3) | (-1,-2) | (-1,-1) | (-1,1) | | 1 | (1,-3) | (1,-2) | (1,-1) | (1,1) | 共有16种等可能的结果，其中直线y = mx + n不经过第四象限的结果有(1,1)，共1种，
∴直线y = mx + n不经过第四象限的概率是$\frac{1}{16}$。