第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9.(2024四川德阳中考,8,★☆☆)已知,正六边形ABC - DEF的面积为6$\sqrt{3}$,则正六边形的边长为(M9224012)( )
A.1
B.$\sqrt{3}$
C.2
D.4
A.1
B.$\sqrt{3}$
C.2
D.4
答案:
C:如图,连接OA,OB,过点O作$OM\perp AB$,垂足为点M,因为六边形ABCDEF是正六边形,所以$\angle AOB=\frac{360^{\circ}}{6}=60^{\circ}$,因为$OA = OB$,所以$\triangle AOB$是正三角形,所以$OA = OB = AB$,设$AB = x$,则$OA = OB = x$,所以$S_{正六边形}=6S_{\triangle AOB}=6\sqrt{3}$,所以$6\times\frac{1}{2}\times x\times\frac{\sqrt{3}}{2}x = 6\sqrt{3}$,解得$x = 2$或$x = - 2$(舍去),即正六边形的边长为2。故选C。
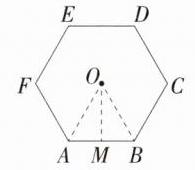
C:如图,连接OA,OB,过点O作$OM\perp AB$,垂足为点M,因为六边形ABCDEF是正六边形,所以$\angle AOB=\frac{360^{\circ}}{6}=60^{\circ}$,因为$OA = OB$,所以$\triangle AOB$是正三角形,所以$OA = OB = AB$,设$AB = x$,则$OA = OB = x$,所以$S_{正六边形}=6S_{\triangle AOB}=6\sqrt{3}$,所以$6\times\frac{1}{2}\times x\times\frac{\sqrt{3}}{2}x = 6\sqrt{3}$,解得$x = 2$或$x = - 2$(舍去),即正六边形的边长为2。故选C。

10.跨化学·苯环 (2024安徽合肥蜀山二模,5,★☆☆)苯(分子式为C₆H₆)的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子组成了一个完美的正六边形(如图1),图2是其平面示意图,点O为正六边形ABCDEF的中心,则∠CBF - ∠COD的度数为(M9224012)( )


A.30°
B.45°
C.60°
D.90°


A.30°
B.45°
C.60°
D.90°
答案:
A:因为六边形ABCDEF是正六边形,所以$\angle A=\angle ABC=\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$,因为$AB = AF$,所以$\angle ABF=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}$,所以$\angle CBF=\angle ABC-\angle ABF = 120^{\circ}-30^{\circ}=90^{\circ}$,因为$\angle COD=\frac{1}{6}\times360^{\circ}=60^{\circ}$,所以$\angle CBF-\angle COD=90^{\circ}-60^{\circ}=30^{\circ}$。故选A。
11.情境题·数学文化 (2023福建中考,10,★☆☆)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,⊙O的半径为1,运用“割圆术”以圆内接正六边形的面积近似估计⊙O的面积,可得π的估计值为$\frac{3\sqrt{3}}{2}$,若用圆内接正十二边形作近似估计,可得π的估计值为( )
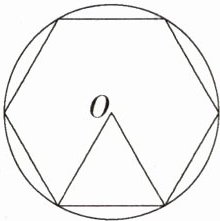
A.$\sqrt{3}$
B.2$\sqrt{2}$
C.3
D.2$\sqrt{3}$

A.$\sqrt{3}$
B.2$\sqrt{2}$
C.3
D.2$\sqrt{3}$
答案:
C:如图,AB是正十二边形的一条边,点O是正十二边形的中心,过A作$AM\perp OB$于M,在正十二边形中,$\angle AOB = 360^{\circ}\div12 = 30^{\circ}$,所以$AM=\frac{1}{2}OA=\frac{1}{2}$,所以$S_{\triangle AOB}=\frac{1}{2}OB\cdot AM=\frac{1}{2}\times1\times\frac{1}{2}=\frac{1}{4}$,所以正十二边形的面积为$12\times\frac{1}{4}=3$,所以$3 = 1^{2}\times\pi$,所以$\pi = 3$,所以$\pi$的估计值为3。故选C。
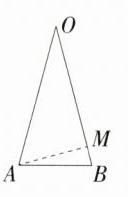
C:如图,AB是正十二边形的一条边,点O是正十二边形的中心,过A作$AM\perp OB$于M,在正十二边形中,$\angle AOB = 360^{\circ}\div12 = 30^{\circ}$,所以$AM=\frac{1}{2}OA=\frac{1}{2}$,所以$S_{\triangle AOB}=\frac{1}{2}OB\cdot AM=\frac{1}{2}\times1\times\frac{1}{2}=\frac{1}{4}$,所以正十二边形的面积为$12\times\frac{1}{4}=3$,所以$3 = 1^{2}\times\pi$,所以$\pi = 3$,所以$\pi$的估计值为3。故选C。

12.(2021内蒙古赤峰中考,17,★☆☆)如图,在拧开一个边长为a的正六边形螺帽时,扳手的开口宽度b = 20 mm,则边长a =_______mm.
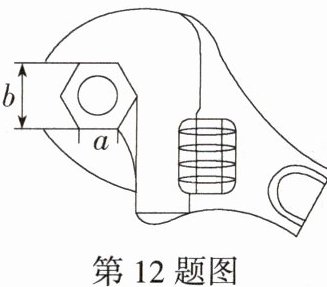

答案:
答案:$\frac{20\sqrt{3}}{3}$ 解析:如图,设正六边形的中心为O,连接OC、OD,过O作$OH\perp CD$于H,则$\angle COD=\frac{360^{\circ}}{6}=60^{\circ}$,所以$\angle COH=\frac{1}{2}\angle COD = 30^{\circ}$,因为$OC = OD$,所以$\triangle OCD$是等边三角形,因为$OH\perp CD$,所以$CH = DH=\frac{1}{2}CD=\frac{a}{2}mm$,易知$OH=\frac{b}{2}=10mm$,所以$CH = 10\times\tan30^{\circ}=\frac{10\sqrt{3}}{3}mm$,所以$a = 2CH=\frac{20\sqrt{3}}{3}mm$。
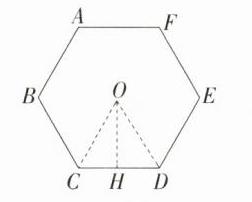
答案:$\frac{20\sqrt{3}}{3}$ 解析:如图,设正六边形的中心为O,连接OC、OD,过O作$OH\perp CD$于H,则$\angle COD=\frac{360^{\circ}}{6}=60^{\circ}$,所以$\angle COH=\frac{1}{2}\angle COD = 30^{\circ}$,因为$OC = OD$,所以$\triangle OCD$是等边三角形,因为$OH\perp CD$,所以$CH = DH=\frac{1}{2}CD=\frac{a}{2}mm$,易知$OH=\frac{b}{2}=10mm$,所以$CH = 10\times\tan30^{\circ}=\frac{10\sqrt{3}}{3}mm$,所以$a = 2CH=\frac{20\sqrt{3}}{3}mm$。

13.(2024四川宜宾中考,15,★☆☆)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长是_______.


答案:
答案:$2\sqrt{5}+2$ 解析:连接BE交AC于O,如图。因为五边形ABCDE是正五边形,所以$\angle CBA=\angle BAE=(5 - 2)\times180^{\circ}\div5 = 108^{\circ}$,$BC = AB = AE$,所以$\angle BCA=\angle BAC=\angle ABE=\angle AEB=(180^{\circ}-108^{\circ})\div2 = 36^{\circ}$,所以$\angle CBO=\angle ABC-\angle ABE = 108^{\circ}-36^{\circ}=72^{\circ}$,所以$\angle BOC = 180^{\circ}-\angle CBO-\angle BCA = 180^{\circ}-72^{\circ}-36^{\circ}=72^{\circ}$,所以$\angle CBO=\angle BOC$,所以$CO = BC = 4$,因为$\angle BAO=\angle CAB$,$\angle ABO = 36^{\circ}=\angle ACB$,所以$\triangle ABO\sim\triangle ACB$,所以$\frac{AB}{AC}=\frac{AO}{AB}$,即$\frac{4}{AC}=\frac{AC - 4}{4}$,解得$AC = 2\sqrt{5}+2$或$AC = 2 - 2\sqrt{5}$(舍去),经检验,$AC = 2\sqrt{5}+2$符合题意。
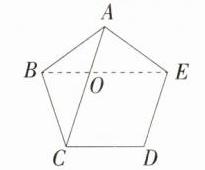
答案:$2\sqrt{5}+2$ 解析:连接BE交AC于O,如图。因为五边形ABCDE是正五边形,所以$\angle CBA=\angle BAE=(5 - 2)\times180^{\circ}\div5 = 108^{\circ}$,$BC = AB = AE$,所以$\angle BCA=\angle BAC=\angle ABE=\angle AEB=(180^{\circ}-108^{\circ})\div2 = 36^{\circ}$,所以$\angle CBO=\angle ABC-\angle ABE = 108^{\circ}-36^{\circ}=72^{\circ}$,所以$\angle BOC = 180^{\circ}-\angle CBO-\angle BCA = 180^{\circ}-72^{\circ}-36^{\circ}=72^{\circ}$,所以$\angle CBO=\angle BOC$,所以$CO = BC = 4$,因为$\angle BAO=\angle CAB$,$\angle ABO = 36^{\circ}=\angle ACB$,所以$\triangle ABO\sim\triangle ACB$,所以$\frac{AB}{AC}=\frac{AO}{AB}$,即$\frac{4}{AC}=\frac{AC - 4}{4}$,解得$AC = 2\sqrt{5}+2$或$AC = 2 - 2\sqrt{5}$(舍去),经检验,$AC = 2\sqrt{5}+2$符合题意。

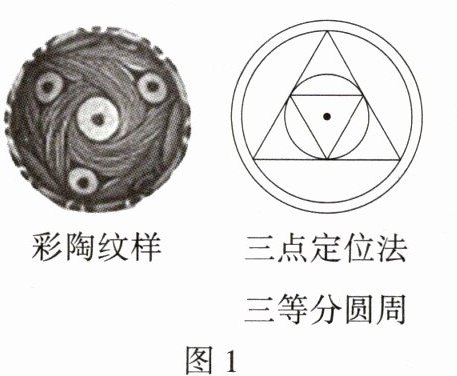
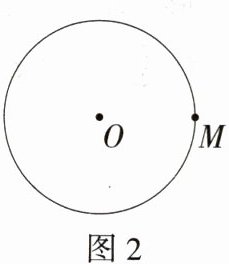
14.跨历史·彩陶 (2024甘肃中考,20,★☆☆)马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.图1中的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知⊙O和圆上一点M.作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法).
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2 cm,则△ABC的周长为_______cm.
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法).
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2 cm,则△ABC的周长为_______cm.


答案:
解析: (1)如图,点A,B,C即为所求。 (2)如图,连接OA,OB,设CM交AB于点E。因为$\overset{\frown}{AB}=\overset{\frown}{AC}=\overset{\frown}{BC}$,所以$AB = CB = AC$,$\angle AOB = 120^{\circ}$,因为CM为直径,所以$\overset{\frown}{CAM}=\overset{\frown}{CBM}$,所以$\overset{\frown}{CAM}-\overset{\frown}{AC}=\overset{\frown}{CBM}-\overset{\frown}{BC}$,即$\overset{\frown}{AM}=\overset{\frown}{BM}$,所以$\angle AOM=\angle BOM = 60^{\circ}$,$OE\perp AB$,所以$AE = EB = AO\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}(cm)$,所以$AB = 2\sqrt{3}cm$,所以$\triangle ABC$的周长为$6\sqrt{3}cm$。故填$6\sqrt{3}$。
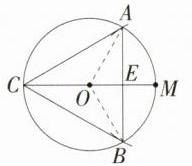
解析: (1)如图,点A,B,C即为所求。 (2)如图,连接OA,OB,设CM交AB于点E。因为$\overset{\frown}{AB}=\overset{\frown}{AC}=\overset{\frown}{BC}$,所以$AB = CB = AC$,$\angle AOB = 120^{\circ}$,因为CM为直径,所以$\overset{\frown}{CAM}=\overset{\frown}{CBM}$,所以$\overset{\frown}{CAM}-\overset{\frown}{AC}=\overset{\frown}{CBM}-\overset{\frown}{BC}$,即$\overset{\frown}{AM}=\overset{\frown}{BM}$,所以$\angle AOM=\angle BOM = 60^{\circ}$,$OE\perp AB$,所以$AE = EB = AO\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}(cm)$,所以$AB = 2\sqrt{3}cm$,所以$\triangle ABC$的周长为$6\sqrt{3}cm$。故填$6\sqrt{3}$。

查看更多完整答案,请扫码查看


