《2025年5年中考3年模拟九年级数学下册沪科版》

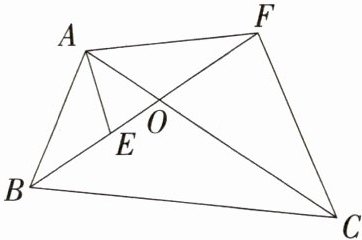
20.[答案含评分细则](2024安徽临泉期末)(7分)如图，已知∠BAC = ∠EAF，∠ABE = ∠ACF，B，E，F三点共线，线段EF与AC交于点O.
(1)求证：△ABE∽△ACF.
(2)若AB = 3，CF = 4，△AOB的面积为9，求△COF的面积.

答案： 解析：
(1)证明：因为∠BAC = ∠EAF，所以∠BAE = ∠CAF，又因为∠ABE = ∠ACF，所以△ABE∽△ACF。
(2)因为∠ABE = ∠ACF，∠AOB = ∠COF，所以△AOB∽△FOC，所以 S△AOB : S△FOC = ($\frac{AB}{CF}$)² = $\frac{9}{16}$，因为 S△AOB = 9，所以 S△FOC = 16。

21.[答案含评分细则](2024安徽和县期末)(8分)国际数学家大会是由国际数学联盟主办的国际数学界规模最大也是最重要的会议，每四年举行一次，被誉为“数学界的奥林匹克盛会”.李颖和汪洋两人想通过玩游戏的方式，了解关于国际数学家大会的一些常识，他们在一个不透明的袋子里装了四个分别标有A、B、C、D的小球，这些小球除所标字母不同外其他都相同，汪洋先从四个小球中随机摸出一个，李颖再从剩下的三个小球中随机摸出一个，然后两人各自回答自己所摸小球上字母对应的问题.
(1)汪洋随机摸出的一个小球是小球A的概率为_______.
(2)请用列表或画树状图的方法求两人摸到的小球恰好标有A、B的概率.

答案：
解析：
(1)$\frac{1}{4}$。
(2)画树状图如图

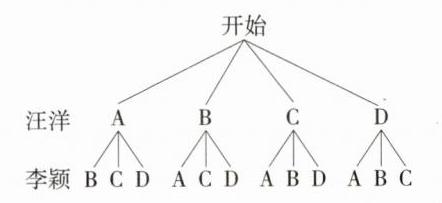
 由树状图可知，共有 12 种等可能的结果，其中两人摸到的小球恰好标有 A、B 的情况有 2 种，所以所求概率为$\frac{2}{12}=\frac{1}{6}$。