第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024广东兴宁月考)已知圆锥的母线长为10,侧面展开图面积为60π,则该圆锥的底面圆的半径长等于 ( )
A.4
B.6
C.8
D.12
A.4
B.6
C.8
D.12
答案:
B 设圆锥的底面半径为R,则圆锥的底面周长 = 2πR,圆锥的侧面展开图的面积 = $\frac{1}{2}$×2πR×10 = 60π,
∴ R = 6. 故选B.
∴ R = 6. 故选B.
2.一题多解(2024广西河池三模)如图,要用一个扇形纸片围成一个圆锥的侧面(接缝处忽略不计),若该圆锥的底面圆周长为8π cm,侧面积为72π cm²,则这个扇形的圆心角的度数是 (M9224013) ( )

A.70°
B.80°
C.90°
D.100°

A.70°
B.80°
C.90°
D.100°
答案:
B 设圆锥的母线长为l,底面圆半径为r,侧面展开图的扇形圆心角为θ°.\n【解法一】 由2πr = 8π,得r = 4. 由π×4l = 72π,得l = 18. 由$\frac{θ\cdot π\cdot 18}{180}$ = 8π,得θ = 80.\n【解法二】 由2πr = 8π,得r = 4. 由$\frac{θ\cdot π\cdot l}{180}$ = 8π,得l = $\frac{1440}{θ}$.
∵ π×4×l = 72π,
∴ $\frac{1440×4π}{θ}$ = 72π,
∴ θ = 80. 故选B.
∵ π×4×l = 72π,
∴ $\frac{1440×4π}{θ}$ = 72π,
∴ θ = 80. 故选B.
3.易错题 如图,已知圆柱体底面圆的半径为$\frac{2}{\pi}$,高为2,AB、CD分别是两底面圆的直径.若一只蚂蚁从A点出发,沿圆柱表面爬行到C点,则蚂蚁爬行的最短距离是________.(结果保留根号)
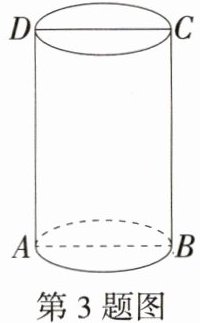

答案:
答案 $2\sqrt{2}$ 解析 如图,沿AD将该圆柱的侧面剪开并展平,则点C落在点C'的位置,由题意知AD = 2,DC' = $\frac{1}{2}$×2π×$\frac{2}{π}$ = 2. 易知蚂蚁爬行的最短距离为AC'的长,AC' = $\sqrt{AD^{2}+DC'^{2}}$ = $\sqrt{2^{2}+2^{2}}$ = $2\sqrt{2}$.
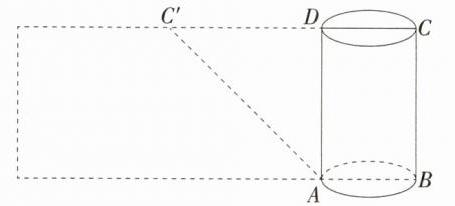
答案 $2\sqrt{2}$ 解析 如图,沿AD将该圆柱的侧面剪开并展平,则点C落在点C'的位置,由题意知AD = 2,DC' = $\frac{1}{2}$×2π×$\frac{2}{π}$ = 2. 易知蚂蚁爬行的最短距离为AC'的长,AC' = $\sqrt{AD^{2}+DC'^{2}}$ = $\sqrt{2^{2}+2^{2}}$ = $2\sqrt{2}$.

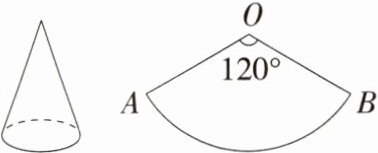
4.如图,已知一个圆锥的侧面展开图是一个半径为9 cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径.
(2)圆锥的全面积.
(1)圆锥的底面半径.
(2)圆锥的全面积.

答案:
解析 \n(1)设该圆锥的底面半径为r cm,根据题意,得2πr = $\frac{120π×9}{180}$,解得r = 3,即该圆锥的底面半径为3 cm.\n(2)
∵ 该圆锥的侧面积 = $\frac{120π×9^{2}}{360}$ = 27π(cm²),圆锥的底面积 = π·3² = 9π(cm²),
∴ 圆锥的全面积为27π + 9π = 36π(cm²).
∵ 该圆锥的侧面积 = $\frac{120π×9^{2}}{360}$ = 27π(cm²),圆锥的底面积 = π·3² = 9π(cm²),
∴ 圆锥的全面积为27π + 9π = 36π(cm²).
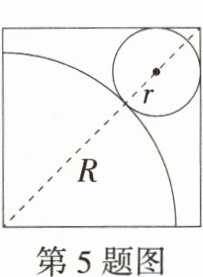
5.(2024广西南宁三中月考,11,★★☆)如图所示,在正方形铁皮上剪下一个圆和一个扇形,使之恰好围成一个圆锥,已知圆的半径为r,扇形的半径为R,则R、r之间的关系为 ( )
A.R = 2r
B.R = $\frac{9}{4}$r
C.R = 3r
D.R = 4r

A.R = 2r
B.R = $\frac{9}{4}$r
C.R = 3r
D.R = 4r
答案:
D 由题意知,扇形的弧长 = $\frac{90πR}{180}$ = $\frac{πR}{2}$,圆的周长为2πr,
∴ $\frac{πR}{2}$ = 2πr,
∴ R = 4r,故选D.
∴ $\frac{πR}{2}$ = 2πr,
∴ R = 4r,故选D.
6.(2023内蒙古赤峰中考,13,★★☆)某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为20π cm,母线AB长为30 cm.为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是 ( )
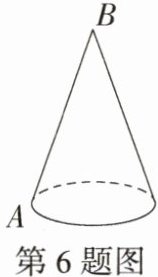
A.30 cm
B.30$\sqrt{3}$ cm
C.60 cm
D.20π cm

A.30 cm
B.30$\sqrt{3}$ cm
C.60 cm
D.20π cm
答案:
B
∵ 圆锥的底面圆周长为20π cm,
∴ 圆锥侧面展开图的扇形的弧长为20π cm,设扇形的圆心角为n°,
∴ $\frac{nπ×30}{180}$ = 20π,解得n = 120,
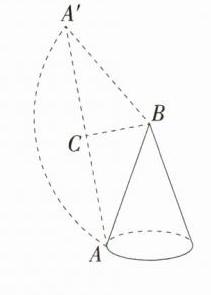
∴ ∠ABA' = 120°,如图,连接AA',过B作BC⊥AA'于点C,
∴ ∠BAA' = 30°,
∴ AC = AB·cos 30° = 30×$\frac{\sqrt{3}}{2}$ = $15\sqrt{3}$(cm),
∴ AA' = 2AC = $30\sqrt{3}$ cm,
∴ 这条彩带的最短长度是$30\sqrt{3}$ cm. 故选B.
B
∵ 圆锥的底面圆周长为20π cm,
∴ 圆锥侧面展开图的扇形的弧长为20π cm,设扇形的圆心角为n°,
∴ $\frac{nπ×30}{180}$ = 20π,解得n = 120,
∴ ∠ABA' = 120°,如图,连接AA',过B作BC⊥AA'于点C,
∴ ∠BAA' = 30°,
∴ AC = AB·cos 30° = 30×$\frac{\sqrt{3}}{2}$ = $15\sqrt{3}$(cm),
∴ AA' = 2AC = $30\sqrt{3}$ cm,
∴ 这条彩带的最短长度是$30\sqrt{3}$ cm. 故选B.

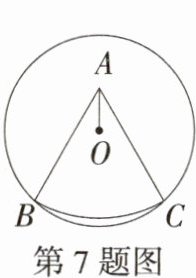
7.(2024安徽马鞍山七中二模,13,★★☆)如图,从一块半径是$\sqrt{13}$ cm的圆形铁皮上剪下一个圆心角(∠BAC)为60°的扇形,将剪下的扇形围成一个圆锥的侧面,若OA = 2 cm,则圆锥的高是________.

答案:
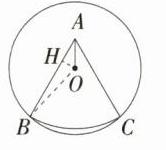
答案 $\frac{\sqrt{105}}{2}$ cm 解析 如图,连接OB,过点O作OH⊥AB于H. 由对称性可知,∠OAH = $\frac{1}{2}$∠BAC = 30°,
∵ ∠AHO = 90°,AO = 2 cm,
∴ OH = $\frac{1}{2}$OA = 1 cm,
∴ AH = $\sqrt{3}$OH = $\sqrt{3}$ cm,
∴ BH = $\sqrt{OB^{2}-OH^{2}}$ = $\sqrt{13 - 1}$ = $2\sqrt{3}$(cm),
∴ AB = $3\sqrt{3}$ cm,
∴ $\overset{\frown}{BC}$的长 = $\frac{60π\cdot 3\sqrt{3}}{180}$ = $\sqrt{3}$π(cm),设圆锥的底面圆的半径为R cm,则2πR = $\sqrt{3}$π,
∴ R = $\frac{\sqrt{3}}{2}$,
∴ 圆锥的高 = $\sqrt{(3\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}$ = $\frac{\sqrt{105}}{2}$(cm).
答案 $\frac{\sqrt{105}}{2}$ cm 解析 如图,连接OB,过点O作OH⊥AB于H. 由对称性可知,∠OAH = $\frac{1}{2}$∠BAC = 30°,
∵ ∠AHO = 90°,AO = 2 cm,
∴ OH = $\frac{1}{2}$OA = 1 cm,
∴ AH = $\sqrt{3}$OH = $\sqrt{3}$ cm,
∴ BH = $\sqrt{OB^{2}-OH^{2}}$ = $\sqrt{13 - 1}$ = $2\sqrt{3}$(cm),
∴ AB = $3\sqrt{3}$ cm,
∴ $\overset{\frown}{BC}$的长 = $\frac{60π\cdot 3\sqrt{3}}{180}$ = $\sqrt{3}$π(cm),设圆锥的底面圆的半径为R cm,则2πR = $\sqrt{3}$π,
∴ R = $\frac{\sqrt{3}}{2}$,
∴ 圆锥的高 = $\sqrt{(3\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}$ = $\frac{\sqrt{105}}{2}$(cm).

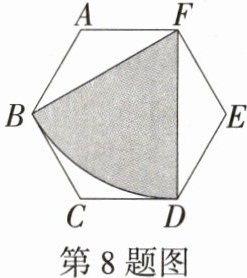
8.(2024山东烟台中考,14,★★☆)如图,在边长为6的正六边形ABCDEF中,以点F为圆心,FB的长为半径作$\overset{\frown}{BD}$,剪下图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为________.(M9224013)

答案:
答案 $\sqrt{3}$ 解析 如图,过点A作AM⊥BF,垂足为M,则BM = FM,
∵ 六边形ABCDEF是正六边形,
∴ ∠BAF = ∠E = $\frac{(6 - 2)×180°}{6}$ = 120°,AB = AF = EF = DE = 6,
∴ ∠ABF = ∠AFB = ∠DFE = $\frac{180° - 120°}{2}$ = 30°,
∴ ∠BFD = 120° - 30° - 30° = 60°,在Rt△ABM中,AB = 6,∠ABM = 30°,
∴ BM = $\frac{\sqrt{3}}{2}$AB = $3\sqrt{3}$,
∴ BF = 2BM = $6\sqrt{3}$,设这个圆锥的底面半径为r,由题意可得,2πr = $\frac{60π×6\sqrt{3}}{180}$,解得r = $\sqrt{3}$.
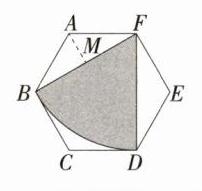
答案 $\sqrt{3}$ 解析 如图,过点A作AM⊥BF,垂足为M,则BM = FM,
∵ 六边形ABCDEF是正六边形,
∴ ∠BAF = ∠E = $\frac{(6 - 2)×180°}{6}$ = 120°,AB = AF = EF = DE = 6,
∴ ∠ABF = ∠AFB = ∠DFE = $\frac{180° - 120°}{2}$ = 30°,
∴ ∠BFD = 120° - 30° - 30° = 60°,在Rt△ABM中,AB = 6,∠ABM = 30°,
∴ BM = $\frac{\sqrt{3}}{2}$AB = $3\sqrt{3}$,
∴ BF = 2BM = $6\sqrt{3}$,设这个圆锥的底面半径为r,由题意可得,2πr = $\frac{60π×6\sqrt{3}}{180}$,解得r = $\sqrt{3}$.

查看更多完整答案,请扫码查看


