第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
7.(2023山东烟台中考,8,★★☆)如图,在正方形中,阴影部分是以正方形的顶点及其对称中心为圆心,以正方形边长的一半为半径作弧形成的封闭图形.一个小球在该正方形内自由滚动,小球随机地停在正方形内的某一点上.若小球停在阴影部分的概率为P1,停在空白部分的概率为P2,则P1与P2的大小关系为 ( )
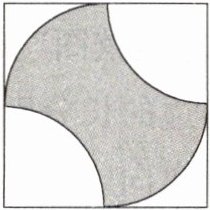
A.P1<P2
B.P1=P2
C.P1>P2
D.无法判断

A.P1<P2
B.P1=P2
C.P1>P2
D.无法判断
答案:
7 B 如图,设正方形的边长为2a,则空白部分的面积为$2\times\frac{1}{4}\times\pi\cdot a^{2}+2(a^{2}-\frac{1}{4}\times\pi\cdot a^{2})=\frac{1}{2}\pi a^{2}+2a^{2}-\frac{1}{2}\pi a^{2}=2a^{2}$,则阴影部分的面积为$(2a)^{2}-2a^{2}=4a^{2}-2a^{2}=2a^{2}$,所以阴影部分的面积 = 空白部分的面积,所以$P_{1}=P_{2}$,故选B。
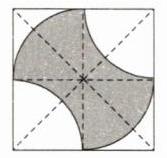
7 B 如图,设正方形的边长为2a,则空白部分的面积为$2\times\frac{1}{4}\times\pi\cdot a^{2}+2(a^{2}-\frac{1}{4}\times\pi\cdot a^{2})=\frac{1}{2}\pi a^{2}+2a^{2}-\frac{1}{2}\pi a^{2}=2a^{2}$,则阴影部分的面积为$(2a)^{2}-2a^{2}=4a^{2}-2a^{2}=2a^{2}$,所以阴影部分的面积 = 空白部分的面积,所以$P_{1}=P_{2}$,故选B。

8.(2024山东威海中考,6,★★☆)如图,在扇形AOB中,∠AOB = 90°,点C是AO的中点.过点C作CE⊥AO交$\overset{\frown}{AB}$于点E,过点E作ED⊥OB,垂足为点D.在扇形内随机选取一点P,则点P落在阴影部分的概率是 ( )
A. $\frac{1}{4}$ B. $\frac{1}{3}$ C. $\frac{1}{2}$ D. $\frac{2}{3}$
A
C E
O D B
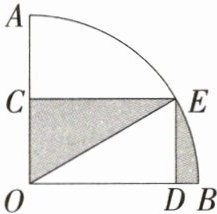
A. $\frac{1}{4}$ B. $\frac{1}{3}$ C. $\frac{1}{2}$ D. $\frac{2}{3}$
A
C E
O D B

答案:
8 B 设⊙O的半径为r,
∵CE⊥AO,
∴∠OCE = 90°。
∵点C是AO的中点,
∴$OC=\frac{1}{2}OA=\frac{1}{2}OE$。在Rt△OCE中,
∵$\cos\angle COE=\frac{OC}{OE}=\frac{1}{2}$,
∴∠COE = 60°,
∴∠BOE = ∠AOB - ∠COE = 30°。
∵ED⊥OB,
∴∠ODE = 90°。
∵∠COD = ∠OCE = 90°,
∴四边形OCED为矩形,
∴$S_{\triangle OCE}=S_{\triangle ODE}$,
∴阴影部分的面积=$S_{扇形BOE}=\frac{30\times\pi\times r^{2}}{360}$,
∴点P落在阴影部分的概率=$\frac{S_{扇形BOE}}{S_{扇形AOB}}=\frac{\frac{30\times\pi\times r^{2}}{360}}{\frac{90\times\pi\times r^{2}}{360}}=\frac{1}{3}$。故选B。
∵CE⊥AO,
∴∠OCE = 90°。
∵点C是AO的中点,
∴$OC=\frac{1}{2}OA=\frac{1}{2}OE$。在Rt△OCE中,
∵$\cos\angle COE=\frac{OC}{OE}=\frac{1}{2}$,
∴∠COE = 60°,
∴∠BOE = ∠AOB - ∠COE = 30°。
∵ED⊥OB,
∴∠ODE = 90°。
∵∠COD = ∠OCE = 90°,
∴四边形OCED为矩形,
∴$S_{\triangle OCE}=S_{\triangle ODE}$,
∴阴影部分的面积=$S_{扇形BOE}=\frac{30\times\pi\times r^{2}}{360}$,
∴点P落在阴影部分的概率=$\frac{S_{扇形BOE}}{S_{扇形AOB}}=\frac{\frac{30\times\pi\times r^{2}}{360}}{\frac{90\times\pi\times r^{2}}{360}}=\frac{1}{3}$。故选B。
9.(2024四川成都天府七中月考,21,★★☆)如图,在☉O的内接正方形ABCD中,AB = 2,以点A为圆心,AD长为半径画弧,得到$\overset{\frown}{BD}$,现假设可以在☉O中随意取点,每个点被取到的机会是相等的,则这个点在阴影区域的概率是________.
D
A O C
B
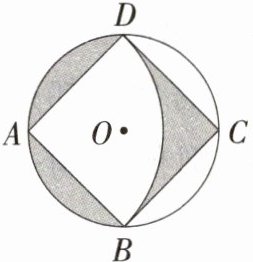
D
A O C
B

答案:
答案 $\frac{1}{\pi}$ 解析 如图,连接BD,
∵∠BAD = 90°,
∴BD是⊙O的直径,
∵AB = 2 = AD,
∴$BD=\sqrt{2}AB = 2\sqrt{2}$,
∴⊙O的半径为$\sqrt{2}$,
∴$S_{\odot O}=(\sqrt{2})^{2}\cdot\pi = 2\pi$,$S_{阴影部分}=S_{半圆O}-S_{弓形BD}=\frac{1}{2}\pi\times(\sqrt{2})^{2}-(\frac{90\times\pi\times2^{2}}{360}-\frac{1}{2}\times2\times2)=\pi - (\pi - 2)=2$,
∴这个点在阴影区域的概率是$\frac{2}{2\pi}=\frac{1}{\pi}$。

答案 $\frac{1}{\pi}$ 解析 如图,连接BD,
∵∠BAD = 90°,
∴BD是⊙O的直径,
∵AB = 2 = AD,
∴$BD=\sqrt{2}AB = 2\sqrt{2}$,
∴⊙O的半径为$\sqrt{2}$,
∴$S_{\odot O}=(\sqrt{2})^{2}\cdot\pi = 2\pi$,$S_{阴影部分}=S_{半圆O}-S_{弓形BD}=\frac{1}{2}\pi\times(\sqrt{2})^{2}-(\frac{90\times\pi\times2^{2}}{360}-\frac{1}{2}\times2\times2)=\pi - (\pi - 2)=2$,
∴这个点在阴影区域的概率是$\frac{2}{2\pi}=\frac{1}{\pi}$。

10.应用意识 小麦高秆(D)对矮秆(d)为显性,抗病(T)对易感病(t)为显性,两对基因可以自由组合.用纯种的高秆抗病(DDTT)小麦和矮秆易感病(ddtt)小麦作亲本,则子二代中选育出的矮秆抗病类型中,能稳定遗传(亲代自交,不会出现性状分离)的概率为 ( )
A. $\frac{1}{16}$
B. $\frac{3}{16}$
C. $\frac{2}{3}$
D. $\frac{1}{3}$
A. $\frac{1}{16}$
B. $\frac{3}{16}$
C. $\frac{2}{3}$
D. $\frac{1}{3}$
答案:
10 D 已知小麦高秆(D)对矮秆(d)为显性,抗病(T)对易感病(t)为显性,两对基因可以自由组合,则纯种高秆抗病小麦DDTT和矮秆
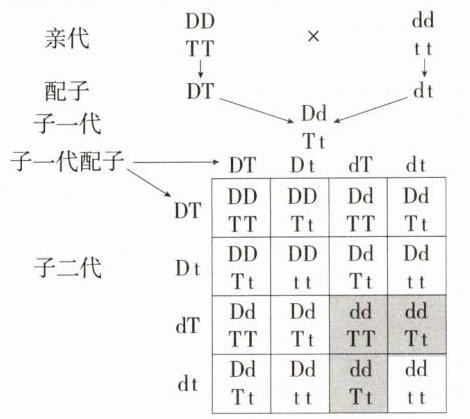
即子二代中矮秆抗病类型有ddTT、ddTt、ddTt三种,其中能够稳定遗传的只有ddTT一种,即稳定遗传的概率为$\frac{1}{3}$。故选D。
10 D 已知小麦高秆(D)对矮秆(d)为显性,抗病(T)对易感病(t)为显性,两对基因可以自由组合,则纯种高秆抗病小麦DDTT和矮秆

即子二代中矮秆抗病类型有ddTT、ddTt、ddTt三种,其中能够稳定遗传的只有ddTT一种,即稳定遗传的概率为$\frac{1}{3}$。故选D。
11.模型观念 有一类随机事件概率的计算方法:设试验结果落在某个区域S中的每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)=$\frac{M的面积}{S的面积}$.有一块边长为30 cm的正方形ABCD飞镖游戏板,假设飞镖投在游戏板上的每一点的机会均等.
(1)在飞镖游戏板上画有半径为5 cm的一个圆(如图),求飞镖落在圆内的概率.
(2)飞镖在游戏板上的落点记为点O,求△OAB为钝角三角形的概率.
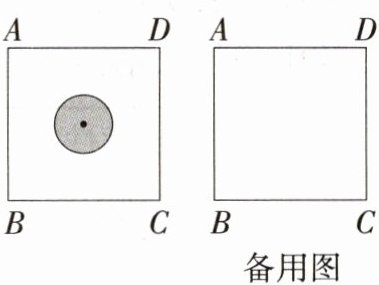
(1)在飞镖游戏板上画有半径为5 cm的一个圆(如图),求飞镖落在圆内的概率.
(2)飞镖在游戏板上的落点记为点O,求△OAB为钝角三角形的概率.

答案:
解析 (1)
∵半径为5 cm的圆的面积=$\pi\cdot5^{2}=25\pi cm^{2}$,边长为30 cm的正方形ABCD的面积=$30^{2}=900 cm^{2}$,
∴P(飞镖落在圆内)=$\frac{25\pi}{900}=\frac{\pi}{36}$。 (2)如图,可得当点O落在以AB为直径的半圆内时,△OAB为钝角三角形。

∵$S_{半圆}=\frac{1}{2}\times\pi\times15^{2}=\frac{225}{2}\pi cm^{2}$,
∴P(△OAB为钝角三角形)=$\frac{\frac{225}{2}\pi}{900}=\frac{\pi}{8}$。
解析 (1)
∵半径为5 cm的圆的面积=$\pi\cdot5^{2}=25\pi cm^{2}$,边长为30 cm的正方形ABCD的面积=$30^{2}=900 cm^{2}$,
∴P(飞镖落在圆内)=$\frac{25\pi}{900}=\frac{\pi}{36}$。 (2)如图,可得当点O落在以AB为直径的半圆内时,△OAB为钝角三角形。

∵$S_{半圆}=\frac{1}{2}\times\pi\times15^{2}=\frac{225}{2}\pi cm^{2}$,
∴P(△OAB为钝角三角形)=$\frac{\frac{225}{2}\pi}{900}=\frac{\pi}{8}$。
查看更多完整答案,请扫码查看


