《2025年5年中考3年模拟九年级数学下册沪科版》

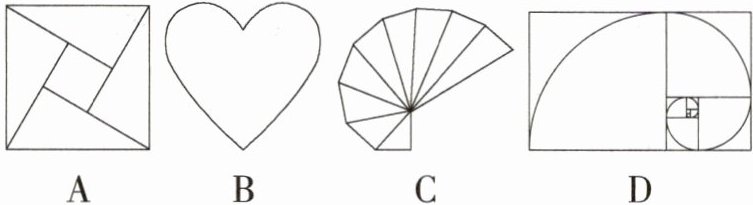
1. 情境题·数学文化(2023广西中考)下列数学经典图形中，是中心对称图形的是 ( )

答案： A.选项B、C、D中的图形都不能找到一个点，使图形绕该点旋转180°后与原来的图形重合，所以不是中心对称图形。选项A中的图形能找到一个点，使图形绕该点旋转180°后与原来的图形重合，所以是中心对称图形。故选A。

2. 新独家原创 小明和小亮在玩一种游戏，两人分别用一个小球向事先画好的圆圈内投掷，两人各投一次，如果一人投进，另一人投不进，则投进的人胜利；如果两人同时投进或同时投不进，则算作平局. 在一次游戏中，小明取得了胜利，如果把小球看作一个点，则小亮投出的结果中小球和圆圈的位置可以看作 ( )
A. 点在圆内
B. 点在圆外
C. 点在圆上
D. 无法判断

答案： B.因为小明取得了胜利，所以小亮投出的球落在圆圈外，对应的位置关系是点在圆外，故选B。

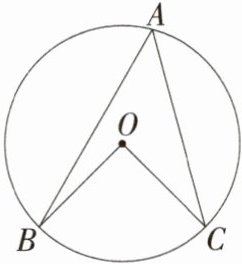
3.(2024湖南中考)如图，AB，AC为⊙O的两条弦，连接OB，OC，若∠A = 45°，则∠BOC的度数为( )

A. 60°
B. 75°
C. 90°
D. 135°

答案： C.
∵$\angle A=\frac{1}{2}\angle BOC$，$\angle A = 45^{\circ}$，
∴$\angle BOC = 2\times45^{\circ}=90^{\circ}$。故选C。

4. 下列条件中，能确定一个圆的是 ( )
A. 以点O为圆心
B. 以点A为圆心，4 cm长为半径
C. 以10 m长为半径
D. 经过已知点M

答案： B.
∵圆心确定，半径确定后才可以确定圆，
∴B选项正确，故选B。

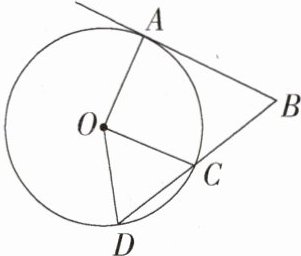
5.(2023黑龙江哈尔滨中考)如图，AB是⊙O的切线，A为切点，连接OA，点C在⊙O上，OC⊥OA，连接BC并延长，交⊙O于点D，连接OD，若∠B = 65°，则∠DOC的度数为 ( )

A. 45°
B. 50°
C. 65°
D. 75°

答案： B.
∵AB是⊙O的切线，A为切点，
∴OA⊥AB，
∵OC⊥OA，
∴AB//OC，
∴$\angle OCD=\angle B = 65^{\circ}$，
∵OC = OD，
∴$\angle OCD=\angle ODC = 65^{\circ}$，
∴$\angle DOC = 180^{\circ}-65^{\circ}-65^{\circ}=50^{\circ}$。故选B。

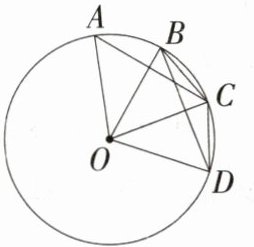
6.(2024上海长宁二模)如图，已知点A、B、C、D都在⊙O上，OB⊥AC，BC = CD，下列说法错误的是 ( )

A. $\overset{\frown}{AB}=\overset{\frown}{BC}$
B. ∠AOD = 3∠BOC
C. AC = 2CD
D. OC⊥BD

答案： C.
∵OB⊥AC，
∴$\overset{\frown}{AB}=\overset{\frown}{BC}$，故A中说法正确，不符合题意；
∵$\overset{\frown}{AB}=\overset{\frown}{BC}$，
∴$\angle AOB=\angle COB$，
∵BC = CD，
∴$\angle BOC=\angle DOC$，
∴$\angle AOD = 3\angle BOC$，故B中说法正确，不符合题意；
∵$\angle AOB=\angle BOC=\angle DOC$，
∴$\angle AOC=\angle BOD$，
∴AC = BD，
∵BD＜BC + CD = 2CD，
∴AC＜2CD，故C中说法错误，符合题意；
∵BC = CD，
∴OC⊥BD，故D中说法正确，不符合题意。故选C。

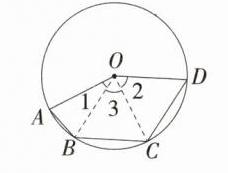
7.(2024黑龙江绥化期末)如图，圆O经过五边形OABCD的四个顶点. 若$\overset{\frown}{AD}$为150°，∠A = 75°，∠D = 60°，则$\overset{\frown}{BC}$的度数为 ( )

A. 25°
B. 40°
C. 50°
D. 60°

答案：
D.连接OB、OC，
∵OA = OB = OC = OD，
∴△OAB、△OBC、△OCD皆为等腰三角形，
∵$\angle A = 75^{\circ}$，$\angle D = 60^{\circ}$，
∴$\angle 1 = 180^{\circ}-2\angle A = 180^{\circ}-2\times75^{\circ}=30^{\circ}$，$\angle 2 = 180^{\circ}-2\angle D = 180^{\circ}-2\times60^{\circ}=60^{\circ}$，
∵$\overset{\frown}{AD}$为150°，
∴$\angle AOD = 150^{\circ}$，
∴$\angle 3=\angle AOD-\angle 1-\angle 2 = 150^{\circ}-30^{\circ}-60^{\circ}=60^{\circ}$，
∴$\overset{\frown}{BC}$的度数为60°。故选D。

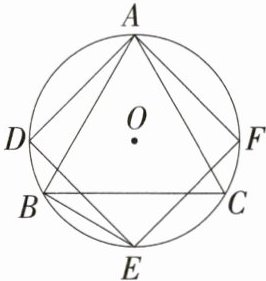
8.(2024江西崇义期末)如图，等边三角形ABC和正方形ADEF都内接于⊙O，则∠BED的度数为 ( )

A. 45°
B. 30°
C. 20°
D. 15°

答案： D.
∵△ABC是等边三角形，
∴A，B，C把⊙O三等分，
∴$\overset{\frown}{AB}$的度数=$\frac{1}{3}\times360^{\circ}=120^{\circ}$，
∵四边形ADEF是正方形，
∴A，D，E，F把⊙O四等分，
∴$\overset{\frown}{AD}$的度数=$\frac{1}{4}\times360^{\circ}=90^{\circ}$，
∴$\overset{\frown}{BD}$的度数=$120^{\circ}-90^{\circ}=30^{\circ}$，
∴$\angle BED=\frac{1}{2}\times30^{\circ}=15^{\circ}$，故选D。