第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9.推理能力 新考向·阅读理解试题 (2024河南开封二模)小明同学学习了《圆》这一章后,对圆的数学史产生了兴趣,下面是他整理的相关材料.

请结合以上材料与所学知识回答下列问题:
(1)根据图(2),运用材料一的内容,完成对材料二的证明.
已知:直线AP是⊙O的一条割线,与⊙O交于点A,B,PT与⊙O相切,切点为T,求证:________.
证明:……
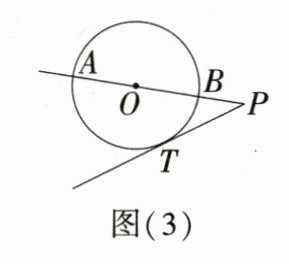
(2)将图(2)中的直线AP绕点P旋转至过圆心O,如图(3),恰好AB∶BP = 3∶1,若PT的长为2$\sqrt{3}$,求BP的长.

请结合以上材料与所学知识回答下列问题:
(1)根据图(2),运用材料一的内容,完成对材料二的证明.
已知:直线AP是⊙O的一条割线,与⊙O交于点A,B,PT与⊙O相切,切点为T,求证:________.
证明:……
(2)将图(2)中的直线AP绕点P旋转至过圆心O,如图(3),恰好AB∶BP = 3∶1,若PT的长为2$\sqrt{3}$,求BP的长.

答案:
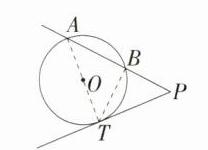
解析 (1)已知:直线AP是⊙O的一条割线,与⊙O交于点A,B,PT与⊙O相切,切点为T,求证:PT² = PA·PB. 证明:如图,连接AT,BT,易得∠BTP = ∠PAT,因为∠P = ∠P,所以△BPT∽△TPA,所以$\frac{PB}{PT}=\frac{PT}{PA}$,所以PT² = PA·PB. (2)设BP = x,则AB = 3x,所以PA = 4x. 因为PA·PB = PT²,PT = $2\sqrt{3}$,所以4x·x = $(2\sqrt{3})^2$,解得$x_1=\sqrt{3}$,$x_2 = -\sqrt{3}$(舍),所以BP = $\sqrt{3}$.
解析 (1)已知:直线AP是⊙O的一条割线,与⊙O交于点A,B,PT与⊙O相切,切点为T,求证:PT² = PA·PB. 证明:如图,连接AT,BT,易得∠BTP = ∠PAT,因为∠P = ∠P,所以△BPT∽△TPA,所以$\frac{PB}{PT}=\frac{PT}{PA}$,所以PT² = PA·PB. (2)设BP = x,则AB = 3x,所以PA = 4x. 因为PA·PB = PT²,PT = $2\sqrt{3}$,所以4x·x = $(2\sqrt{3})^2$,解得$x_1=\sqrt{3}$,$x_2 = -\sqrt{3}$(舍),所以BP = $\sqrt{3}$.

10.模型观念 (2021四川遂宁中考)已知平面直角坐标系中,点P(x₀,y₀)和直线Ax + By + C = 0(其中A,B不全为0),则点P到直线Ax + By + C = 0的距离可用公式d = $\frac{|Ax_{0}+By_{0}+C|}{\sqrt{A^{2}+B^{2}}}$来计算.
例如:求点P(1,2)到直线y = 2x + 1的距离,y = 2x + 1可化为2x - y + 1 = 0,其中A = 2,B = -1,C = 1,所以点P(1,2)到直线y = 2x + 1的距离为d = $\frac{|Ax_{0}+By_{0}+C|}{\sqrt{A^{2}+B^{2}}}$ = $\frac{|2×1+(-1)×2+1|}{\sqrt{2^{2}+(-1)^{2}}}$ = $\frac{1}{\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$.
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线y = $\sqrt{3}$x + 9的距离.
(2)在(1)的条件下,⊙M的半径r = 4,判断⊙M与直线y = $\sqrt{3}$x + 9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
例如:求点P(1,2)到直线y = 2x + 1的距离,y = 2x + 1可化为2x - y + 1 = 0,其中A = 2,B = -1,C = 1,所以点P(1,2)到直线y = 2x + 1的距离为d = $\frac{|Ax_{0}+By_{0}+C|}{\sqrt{A^{2}+B^{2}}}$ = $\frac{|2×1+(-1)×2+1|}{\sqrt{2^{2}+(-1)^{2}}}$ = $\frac{1}{\sqrt{5}}$ = $\frac{\sqrt{5}}{5}$.
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线y = $\sqrt{3}$x + 9的距离.
(2)在(1)的条件下,⊙M的半径r = 4,判断⊙M与直线y = $\sqrt{3}$x + 9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
答案:
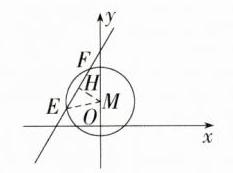
解析 (1)$y = \sqrt{3}x + 9$可变形为$\sqrt{3}x - y + 9 = 0$,其中A = $\sqrt{3}$,B = -1,C = 9,由公式得,点M(0,3)到直线$y = \sqrt{3}x + 9$的距离$d = \frac{|\sqrt{3}×0 - 3 + 9|}{\sqrt{(\sqrt{3})^2 + (-1)^2}} = 3$,所以点M(0,3)到直线$y = \sqrt{3}x + 9$的距离为3. (2)相交. 由(1)可知,圆心M到直线$y = \sqrt{3}x + 9$的距离d = 3,因为⊙M的半径r = 4,所以d < r,所以直线$y = \sqrt{3}x + 9$与⊙M相交. 两交点记作E,F,如图, 连接EM,过点M作MH⊥EF于H,则EF = 2EH,在Rt△EHM中,EM = 4,MH = 3,根据勾股定理,得$EH = \sqrt{EM^2 - MH^2} = \sqrt{4^2 - 3^2} = \sqrt{7}$,所以弦长n = EF = 2EH = $2\sqrt{7}$.
解析 (1)$y = \sqrt{3}x + 9$可变形为$\sqrt{3}x - y + 9 = 0$,其中A = $\sqrt{3}$,B = -1,C = 9,由公式得,点M(0,3)到直线$y = \sqrt{3}x + 9$的距离$d = \frac{|\sqrt{3}×0 - 3 + 9|}{\sqrt{(\sqrt{3})^2 + (-1)^2}} = 3$,所以点M(0,3)到直线$y = \sqrt{3}x + 9$的距离为3. (2)相交. 由(1)可知,圆心M到直线$y = \sqrt{3}x + 9$的距离d = 3,因为⊙M的半径r = 4,所以d < r,所以直线$y = \sqrt{3}x + 9$与⊙M相交. 两交点记作E,F,如图, 连接EM,过点M作MH⊥EF于H,则EF = 2EH,在Rt△EHM中,EM = 4,MH = 3,根据勾股定理,得$EH = \sqrt{EM^2 - MH^2} = \sqrt{4^2 - 3^2} = \sqrt{7}$,所以弦长n = EF = 2EH = $2\sqrt{7}$.

查看更多完整答案,请扫码查看


