《2025年5年中考3年模拟九年级数学下册沪科版》

1.若一个四边形既有外接圆，又有内切圆，且这两个圆是同心圆，则这个四边形一定是（ ）
A.平行四边形
B.矩形
C.菱形
D.正方形

答案： D：任何一个正多边形都有一个外接圆和一个内切圆，且这两个圆是同心圆，所以这个四边形是正四边形，即正方形，故选D。

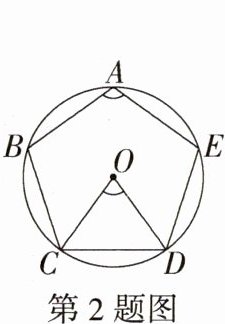
2.(2023安徽中考)如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE - ∠COD =（M9224012）（ ）

A.60°
B.54°
C.48°
D.36°

答案： D：因为五边形ABCDE是正五边形，所以$\angle BAE=\frac{(5 - 2)\times180^{\circ}}{5}=108^{\circ}$，$\angle COD=\frac{360^{\circ}}{5}=72^{\circ}$，所以$\angle BAE-\angle COD=108^{\circ}-72^{\circ}=36^{\circ}$，故选D。

3.(2024广东汕头濠江二模)半径为2的圆的一个内接正多边形的内角为120°，则这个内接正多边形的边长为（ ）
A.1
B.2
C.$\sqrt{3}$
D.2$\sqrt{3}$

答案：
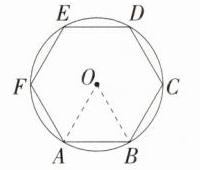
B：因为正多边形的每个内角都相等，且为$120^{\circ}$，所以其一个外角的度数为$180^{\circ}-120^{\circ}=60^{\circ}$，所以这个正多边形的边数为$360^{\circ}\div60^{\circ}=6$。如图，在半径为2的圆O中有内接正六边形ABCDEF，连接OA，OB，易知$\triangle AOB$是等边三角形，所以$AB = OA = 2$，故选B。

4.(2024安徽安庆二模)将刻度尺按如图所示的方式放置在正六边形ABCDEF上，顶点C，F分别对应刻度尺上的刻度12和4，则AB与CF之间的距离为(M9224012)（ ）

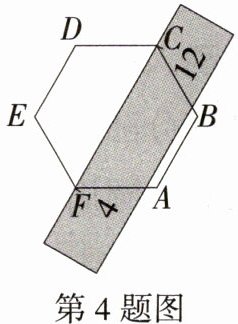
A.8
B.2$\sqrt{3}$
C. 4$\sqrt{3}$
D.4

答案：
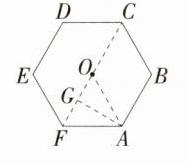
B：如图，设正六边形ABCDEF的中心为O，连接OF，OC，OA，作$AG\perp OF$，垂足为G。由题意可知，$CF = 12 - 4 = 8$，因为六边形ABCDEF是正六边形，所以$\triangle AOF$是正三角形，所以$OF = OC = OA = AF = 4$，所以$AG=\frac{\sqrt{3}}{2}AF = 2\sqrt{3}$，即AB与CF之间的距离为$2\sqrt{3}$。故选B。

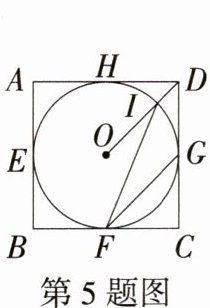
5.新独家原创 如图，四边形ABCD是⊙O外切正方形，切点分别为E、F、G、H，连接OD，交⊙O于点I，连接IF，GF，则∠IFG的度数为_______.

答案： 答案：$22.5^{\circ}$ 解析：连接OH，OG（图略），因为G、H是切点，所以$OG\perp CD$，$OH\perp AD$，$OH = OG$，因为$\angle HDG = 90^{\circ}$，所以四边形OHDG为正方形，所以$\angle DOG = 45^{\circ}$，所以$\angle IFG=\frac{1}{2}\angle DOG = 22.5^{\circ}$。

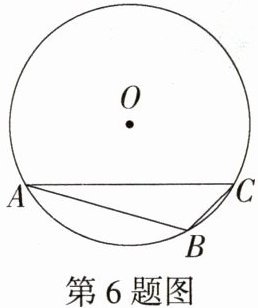
6.易错题 如图，A，B，C是⊙O上的三点，若AC，AB，BC分别是⊙O的内接正三角形，正方形，正n边形的一边，则n =_______.

答案： 答案：12 解析：连接OA，OB，OC（图略）。因为AC，AB分别是$\odot O$内接正三角形、正方形的一边，所以$\angle AOC = 120^{\circ}$，$\angle AOB = 90^{\circ}$，所以$\angle BOC=\angle AOC-\angle AOB = 30^{\circ}$，由题意得$30^{\circ}=\frac{360^{\circ}}{n}$，所以$n = 12$。 易错警示：正n边形的边数等于$360^{\circ}$除以中心角的度数，本题容易把$360^{\circ}$与$\angle BAC$的度数比作为多边形的边数。

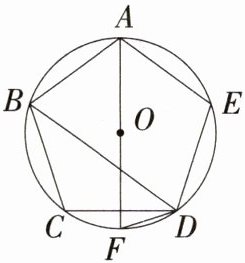
7.如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，求∠BDF的度数.(M9224012)

答案： 解析：因为AF是$\odot O$的直径，五边形ABCDE是$\odot O$的内接正五边形，所以$\overset{\frown}{AB}=\overset{\frown}{AE}$，$\angle BAE = 108^{\circ}$，$\overset{\frown}{ABF}=\overset{\frown}{AEF}$，所以$\overset{\frown}{BF}=\overset{\frown}{EF}$，所以$\angle BAF=\frac{1}{2}\angle BAE = 54^{\circ}$，所以$\angle BDF=\angle BAF = 54^{\circ}$。

8.转化与化归思想 如图①②③，正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形，点M、N分别从点B、C开始，以相同的速度在⊙O上逆时针运动，AM与BN交于点P.

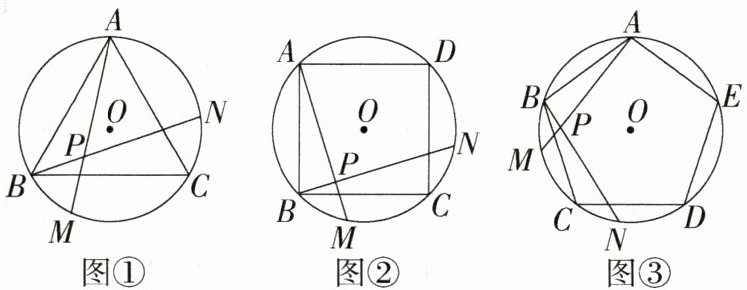
(1)求图①中∠APN的度数.
(2)写出图②中∠APN的度数和图③中∠APN的度数.
(3)试探索∠APN的度数与正多边形边数n的关系(直接写出答案).

答案： 解析： （1）因为$AC = BC$，所以$\overset{\frown}{AC}=\overset{\frown}{BC}$，由题意可得$\overset{\frown}{BM}=\overset{\frown}{CN}$，所以$\overset{\frown}{AN}=\overset{\frown}{CM}$，所以$\angle ABN=\angle MAC$。因为$\angle APN=\angle ABN+\angle BAP$，所以$\angle APN=\angle BAP+\angle MAC=\angle BAC = 60^{\circ}$。 （2）按（1）中的思路可得题图②中，$\angle APN$的度数为$90^{\circ}$；题图③中，$\angle APN$的度数为$108^{\circ}$。 （3）$\angle APN$的度数$=\frac{(n - 2)\cdot180^{\circ}}{n}$。