第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
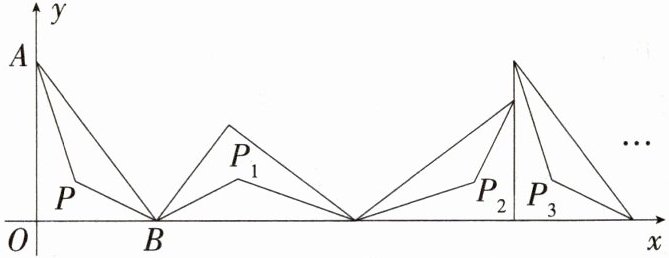
19.推理能力 新考向·规律探究试题 (2024黑龙江齐齐哈尔一模)如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次落在x轴上.点P是Rt△OAB两锐角平分线的交点,第一次滚动后得到的对应点为P₁;第二次滚动后得到的对应点为P₂;……按此规律,点P₂₀₂₄的坐标是________.

答案:
$(8099,1)$。解析:如图,过点$P$作$PD\perp OA$,$PE\perp OB$,$PF\perp AB$,垂足分别为$D$,$E$,$F$,分别过点$P_{1}$,$P_{2}$,$P_{3}$作$P_{1}F_{1}\perp x$轴,$P_{2}D_{1}\perp x$轴,$P_{3}E_{1}\perp x$轴,垂足为$F_{1}$,$D_{1}$,$E_{1}$,以点$P$为圆心,$PD$长为半径作$\odot P$,因为点$P$是$Rt\triangle OAB$两锐角平分线的交点,所以点$P$为$Rt\triangle OAB$的内心,又因为$PD\perp OA$,$PE\perp OB$,$PF\perp AB$,所以$PD = PE = PF$,$AD = AF$,$OD = OE$,$BE = BF$,因为$A(0,4)$,$B(3,0)$,所以$AB = 5$,所以$OD = OE=\frac{OA + OB - AB}{2}=1$,所以$P(1,1)$,因为$PD\perp OA$,$PE\perp OB$,$OD = OE$,所以四边形$PDOE$为正方形,所以$PD = PE = PF = OD = 1$,在$Rt\triangle BP_{1}F_{1}$中,$P_{1}F_{1}=PF = 1$,$BF_{1}=BF = BE = OB - OE = 2$,所以$P_{1}$的横坐标为$3 + 2 = 5$,所以$P_{1}(5,1)$,同理可得,$P_{2}(11,1)$,$P_{3}(13,1)$,$P_{4}(17,1)$,$P_{5}(23,1)$,$P_{6}(25,1)$,……由此可见,每滚动三次为一个循环,且每个循环横坐标增加12(三角形的周长),因为$2024\div3 = 674\cdots\cdots2$,所以$P_{2024}$的横坐标为$674\times12+2 + 2+3 + 3+1 = 8099$,故点$P_{2024}$的坐标为$(8099,1)$。
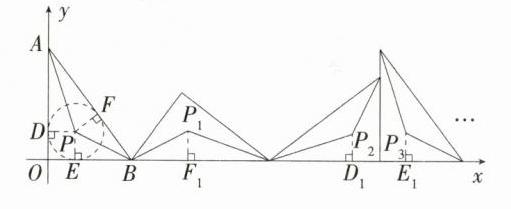
$(8099,1)$。解析:如图,过点$P$作$PD\perp OA$,$PE\perp OB$,$PF\perp AB$,垂足分别为$D$,$E$,$F$,分别过点$P_{1}$,$P_{2}$,$P_{3}$作$P_{1}F_{1}\perp x$轴,$P_{2}D_{1}\perp x$轴,$P_{3}E_{1}\perp x$轴,垂足为$F_{1}$,$D_{1}$,$E_{1}$,以点$P$为圆心,$PD$长为半径作$\odot P$,因为点$P$是$Rt\triangle OAB$两锐角平分线的交点,所以点$P$为$Rt\triangle OAB$的内心,又因为$PD\perp OA$,$PE\perp OB$,$PF\perp AB$,所以$PD = PE = PF$,$AD = AF$,$OD = OE$,$BE = BF$,因为$A(0,4)$,$B(3,0)$,所以$AB = 5$,所以$OD = OE=\frac{OA + OB - AB}{2}=1$,所以$P(1,1)$,因为$PD\perp OA$,$PE\perp OB$,$OD = OE$,所以四边形$PDOE$为正方形,所以$PD = PE = PF = OD = 1$,在$Rt\triangle BP_{1}F_{1}$中,$P_{1}F_{1}=PF = 1$,$BF_{1}=BF = BE = OB - OE = 2$,所以$P_{1}$的横坐标为$3 + 2 = 5$,所以$P_{1}(5,1)$,同理可得,$P_{2}(11,1)$,$P_{3}(13,1)$,$P_{4}(17,1)$,$P_{5}(23,1)$,$P_{6}(25,1)$,……由此可见,每滚动三次为一个循环,且每个循环横坐标增加12(三角形的周长),因为$2024\div3 = 674\cdots\cdots2$,所以$P_{2024}$的横坐标为$674\times12+2 + 2+3 + 3+1 = 8099$,故点$P_{2024}$的坐标为$(8099,1)$。

20.推理能力 (2024湖南长沙中考节选)对于凸四边形,根据它有无外接圆(四个顶点都在同一个圆上)与内切圆(四条边都与同一个圆相切),可分为四种类型,我们不妨约定:既无外接圆,又无内切圆的四边形称为“平凡型无圆”四边形;只有外接圆,而无内切圆的四边形称为“外接型单圆”四边形;只有内切圆,而无外接圆的四边形称为“内切型单圆”四边形;既有外接圆,又有内切圆的四边形称为“完美型双圆”四边形.
请你根据该约定,解答下列问题:
(1)请你判断下列说法是否正确(在题后相应的括号中,正确的打“√”,错误的打“×”).
①平行四边形一定不是“平凡型无圆”四边形; ( )
②内角不等于90°的菱形一定是“内切型单圆”四边形; ( )
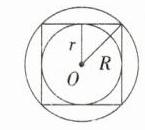
③若“完美型双圆”四边形的外接圆圆心与内切圆圆心重合,外接圆半径为R,内切圆半径为r,则有R = $\sqrt{2}r$. ( )
(2)已知四边形ABCD是“完美型双圆”四边形,它的内切圆☉O与AB,BC,CD,AD分别相切于点E,F,G,H.
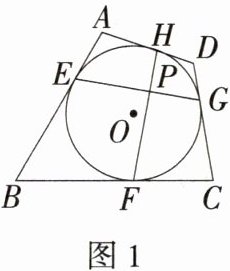
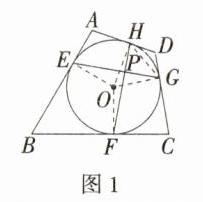
①如图1,连接EG,FH交于点P.求证:EG⊥FH;
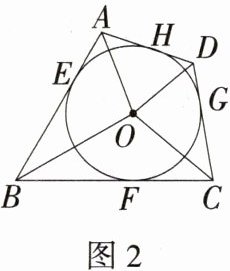
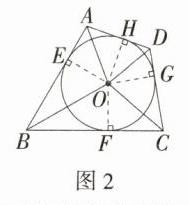
②如图2,连接OA,OB,OC,OD,若OA = 2,OB = 6,OC = 3,求内切圆☉O的半径r及OD的长.
请你根据该约定,解答下列问题:
(1)请你判断下列说法是否正确(在题后相应的括号中,正确的打“√”,错误的打“×”).
①平行四边形一定不是“平凡型无圆”四边形; ( )
②内角不等于90°的菱形一定是“内切型单圆”四边形; ( )
③若“完美型双圆”四边形的外接圆圆心与内切圆圆心重合,外接圆半径为R,内切圆半径为r,则有R = $\sqrt{2}r$. ( )
(2)已知四边形ABCD是“完美型双圆”四边形,它的内切圆☉O与AB,BC,CD,AD分别相切于点E,F,G,H.
①如图1,连接EG,FH交于点P.求证:EG⊥FH;
②如图2,连接OA,OB,OC,OD,若OA = 2,OB = 6,OC = 3,求内切圆☉O的半径r及OD的长.


答案:
解析:
(1)①×.②√.③√.\n**详解**:①当平行四边形无$90^{\circ}$角的内角,且对边长度之和不相等时,该平行四边形既无外接圆,也无内切圆。故平行四边形不一定是“平凡型无圆”四边形,故①错误。\n②由菱形对角线性质:每条对角线会平分一组对角,可知对角线的交点到菱形各边距离相等,但到四个顶点距离不相等。所以内角不等于$90^{\circ}$的菱形有内切圆,无外接圆,故②正确。\n③当“完美型双圆”四边形的外接圆圆心与内切圆圆心重合时,这个四边形为正方形。如图:圆心为正方形对角线的交点,由正方形性质可知$R = \sqrt{2}r$,故③正确。
(2)①**证明**:如图1,连接$OE$,$OF$,$OG$,$OH$,$HG$,因为$\odot O$是四边形$ABCD$的内切圆,所以$OE\perp AB$,$OF\perp BC$,$OG\perp CD$,$OH\perp AD$,所以$\angle OEA=\angle OHA = 90^{\circ}$,所以在四边形$EAHO$中,$\angle A+\angle EOH = 360^{\circ}-90^{\circ}-90^{\circ}=180^{\circ}$。同理可证$\angle FOG+\angle C = 180^{\circ}$。因为四边形$ABCD$是“完美型双圆”四边形,所以四边形$ABCD$有外接圆,所以$\angle A+\angle C = 180^{\circ}$,所以$\angle EOH=\angle C$,所以$\angle FOG+\angle EOH = 180^{\circ}$。又因为$\angle FHG=\frac{1}{2}\angle FOG$,$\angle EGH=\frac{1}{2}\angle EOH$,所以$\angle FHG+\angle EGH = 90^{\circ}$,所以$\angle HPG = 90^{\circ}$,即$EG\perp FH$。 ②如图2,连接$OE$,$OF$,$OG$,$OH$。因为四边形$ABCD$是“完美型双圆”四边形,所以$\angle OAH+\angle OAE+\angle OCG+\angle OCF = 180^{\circ}$。又因为$\odot O$与$AB$,$BC$,$CD$,$AD$分别相切于点$E$,$F$,$G$,$H$,所以$\angle OAH=\angle OAE$,$\angle OCG=\angle OCF$,所以$\angle OAH+\angle OCG = 90^{\circ}$。又因为$\angle COG+\angle OCG = 90^{\circ}$,所以$\angle OAH=\angle COG$。又因为$\angle AHO=\angle OGC = 90^{\circ}$,所以$\triangle AOH\sim\triangle OCG$,所以$\frac{AO}{OC}=\frac{OH}{CG}$,即$\frac{2}{3}=\frac{r}{CG}$,解得$CG=\frac{3}{2}r$。在$Rt\triangle OGC$中,有$OG^{2}+CG^{2}=OC^{2}$,即$r^{2}+(\frac{3}{2}r)^{2}=3^{2}$,解得$r=\frac{6}{13}\sqrt{13}$(负值舍去)。在$Rt\triangle OBE$中,$BE=\sqrt{OB^{2}-r^{2}}=\sqrt{6^{2}-\frac{36}{13}}=\frac{12}{13}\sqrt{39}$。同理可证$\triangle BEO\sim\triangle OHD$,所以$\frac{BE}{OH}=\frac{OB}{OD}$,即$\frac{\frac{12}{13}\sqrt{39}}{\frac{6}{13}\sqrt{13}}=\frac{6}{OD}$,解得$OD=\sqrt{3}$。
解析:
(1)①×.②√.③√.\n**详解**:①当平行四边形无$90^{\circ}$角的内角,且对边长度之和不相等时,该平行四边形既无外接圆,也无内切圆。故平行四边形不一定是“平凡型无圆”四边形,故①错误。\n②由菱形对角线性质:每条对角线会平分一组对角,可知对角线的交点到菱形各边距离相等,但到四个顶点距离不相等。所以内角不等于$90^{\circ}$的菱形有内切圆,无外接圆,故②正确。\n③当“完美型双圆”四边形的外接圆圆心与内切圆圆心重合时,这个四边形为正方形。如图:圆心为正方形对角线的交点,由正方形性质可知$R = \sqrt{2}r$,故③正确。
(2)①**证明**:如图1,连接$OE$,$OF$,$OG$,$OH$,$HG$,因为$\odot O$是四边形$ABCD$的内切圆,所以$OE\perp AB$,$OF\perp BC$,$OG\perp CD$,$OH\perp AD$,所以$\angle OEA=\angle OHA = 90^{\circ}$,所以在四边形$EAHO$中,$\angle A+\angle EOH = 360^{\circ}-90^{\circ}-90^{\circ}=180^{\circ}$。同理可证$\angle FOG+\angle C = 180^{\circ}$。因为四边形$ABCD$是“完美型双圆”四边形,所以四边形$ABCD$有外接圆,所以$\angle A+\angle C = 180^{\circ}$,所以$\angle EOH=\angle C$,所以$\angle FOG+\angle EOH = 180^{\circ}$。又因为$\angle FHG=\frac{1}{2}\angle FOG$,$\angle EGH=\frac{1}{2}\angle EOH$,所以$\angle FHG+\angle EGH = 90^{\circ}$,所以$\angle HPG = 90^{\circ}$,即$EG\perp FH$。 ②如图2,连接$OE$,$OF$,$OG$,$OH$。因为四边形$ABCD$是“完美型双圆”四边形,所以$\angle OAH+\angle OAE+\angle OCG+\angle OCF = 180^{\circ}$。又因为$\odot O$与$AB$,$BC$,$CD$,$AD$分别相切于点$E$,$F$,$G$,$H$,所以$\angle OAH=\angle OAE$,$\angle OCG=\angle OCF$,所以$\angle OAH+\angle OCG = 90^{\circ}$。又因为$\angle COG+\angle OCG = 90^{\circ}$,所以$\angle OAH=\angle COG$。又因为$\angle AHO=\angle OGC = 90^{\circ}$,所以$\triangle AOH\sim\triangle OCG$,所以$\frac{AO}{OC}=\frac{OH}{CG}$,即$\frac{2}{3}=\frac{r}{CG}$,解得$CG=\frac{3}{2}r$。在$Rt\triangle OGC$中,有$OG^{2}+CG^{2}=OC^{2}$,即$r^{2}+(\frac{3}{2}r)^{2}=3^{2}$,解得$r=\frac{6}{13}\sqrt{13}$(负值舍去)。在$Rt\triangle OBE$中,$BE=\sqrt{OB^{2}-r^{2}}=\sqrt{6^{2}-\frac{36}{13}}=\frac{12}{13}\sqrt{39}$。同理可证$\triangle BEO\sim\triangle OHD$,所以$\frac{BE}{OH}=\frac{OB}{OD}$,即$\frac{\frac{12}{13}\sqrt{39}}{\frac{6}{13}\sqrt{13}}=\frac{6}{OD}$,解得$OD=\sqrt{3}$。



查看更多完整答案,请扫码查看


