《2025年5年中考3年模拟九年级数学下册沪科版》

1. 跨语文·作品赏析 巴金的作品《海上日出》中有这样一段文字：“到了最后，终于冲破了云霞，完全跳出了海面，颜色红得非常可爱.”这段文字给我们呈现了直线与圆的哪一种位置关系（M9224009）（ ）
A. 相离
B. 相切
C. 相交
D. 无法确定

答案： A 根据“完全跳出了海面”，可知直线和圆此时是相离的位置关系. 故选A.

2. 教材变式·P36T1 已知⊙O的直径为10，圆心O到直线l的距离为4，则下列能正确反映直线l与⊙O的位置关系的图形是（M9224009）（ ）

答案： B
∵ ⊙O的直径为10，
∴ ⊙O的半径为5，即r = 5，又
∵ 圆心O到直线l的距离为4，即d = 4，
∴ d ＜ r，
∴ 直线l与⊙O相交. 故选B.

3. 易错题（2021浙江嘉兴中考）已知平面内有⊙O和点A，B，若⊙O的半径为2 cm，线段OA = 3 cm，OB = 2 cm，则直线AB与⊙O的位置关系为（ ）
A. 相离
B. 相交
C. 相切
D. 相交或相切

答案： D
∵ ⊙O的半径为2 cm，线段OA = 3 cm，OB = 2 cm，
∴ 点A到圆心O的距离大于圆的半径，点B到圆心O的距离等于圆的半径，
∴ 点A在⊙O外，点B在⊙O上，
∴ 直线AB与⊙O的位置关系为相交或相切，故选D.

4. 面积法 已知Rt△ABC中，∠BCA = 90°，BC = 5 cm，AC = 12 cm，以点C为圆心，作半径为R cm的圆.（M9224009）
（1）当R为何值时，⊙C和直线AB相离？
（2）当R为何值时，⊙C和直线AB相切？
（3）当R为何值时，⊙C和直线AB相交？

答案：
解析 （1）如图，过点C作CD⊥AB于点D，

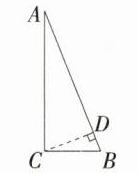
∵ 在Rt△ABC中，∠BCA = 90°，BC = 5 cm，AC = 12 cm，
∴ AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{12^{2}+5^{2}} = 13$ cm，
∴ CD = $\frac{AC\cdot BC}{AB}=\frac{12\times5}{13}=\frac{60}{13}$ cm，
∴ 当0 ＜ R ＜ $\frac{60}{13}$时，⊙C和直线AB相离. （2）当R = $\frac{60}{13}$时，⊙C和直线AB相切. （3）当R ＞ $\frac{60}{13}$时，⊙C和直线AB相交. 方法归纳 圆心到直线的距离和半径的数量关系与直线和圆的位置关系可以互相转化，体现了数形结合思想. 本题在求直角三角形斜边上的高时，用到了面积法，这是求直角三角形斜边上的高的常用方法.

5.（2023江苏宿迁中考，7，★★☆）在同一平面内，已知⊙O的半径为2，圆心O到直线l的距离为3，点P为圆上的一个动点，则点P到直线l的最大距离是（ ）
A. 2
B. 5
C. 6
D. 8

答案：
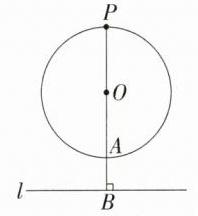
B 如图，由题意得，OA = 2，OB = 3，延长BO与⊙O交于点P，此时点P到直线l的距离最大，最大距离是3 + 2 = 5，故选B.

6.（2024安徽凤阳期末，10，★★☆）如图，已知⊙O是以数轴原点O为圆心，半径为1的圆，∠AOB = 45°，点P在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP = x，则x的取值范围是（ ）

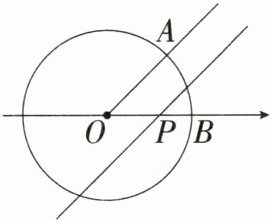
A. -√2 ≤ x ≤ √2
B. 0 ＜ x ≤ √2
C. -1 ≤ x ≤ 1
D. x ＞ √2

答案：
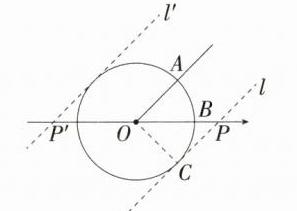
B 如图，当点P在点O右侧，且过点P与OA平行的直线l与⊙O相切时，作OC⊥l，垂足为C，则OC = 1.
∵ ∠AOB = 45°，OA//PC，
∴ ∠OPC = 45°，
∴ PC = OC = 1，
∴ OP = $\sqrt{2}$，同理，当点P在点O左侧的P'处，且过点P'与OA平行的直线l'与⊙O相切时，OP' = $\sqrt{2}$，易知O，P不重合，所以x的取值范围是0 ＜ x ≤ $\sqrt{2}$. 故选B

7.（2024四川绵阳安州期末，18，★★☆）如图所示的是两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是_______.

答案： 答案 8 ≤ AB ≤ 10 解析 当AB是大圆的直径时，AB的值最大，最大值为10. 当AB与小圆相切时，AB的值最小，
∵ 小圆的半径为3，大圆的半径为5，
∴ 此时AB = 2×$\sqrt{5^{2}-3^{2}} = 8$.
∵ 大圆的弦AB与小圆有公共点，即AB与小圆相切或相交，
∴ 8 ≤ AB ≤ 10.

8. 新考法·抛物线与切线综合 易错题（2023安徽无为期末，14，★★☆）如图，已知⊙P的半径为1，圆心P在抛物线y = $\frac{1}{2}x^{2}-1$上运动，当⊙P与x轴相切时，圆心P的坐标为__________.

答案： 答案 （2，1）或（-2，1）或（0，-1） 解析 本题借助抛物线考查直线与圆的位置关系.
∵ ⊙P与x轴相切，⊙P的半径为1，
∴ P到x轴的距离等于1，
∴ 点P的纵坐标为1或 - 1. 当y = 1时，代入可得1 = $\frac{1}{2}x^{2}-1$，解得x = 2或x = - 2，此时P点坐标为（2，1）或（-2，1）；当y = - 1时，代入可得 - 1 = $\frac{1}{2}x^{2}-1$，解得x = 0，此时P点坐标为（0，-1）. 综上可知，P点坐标为（2，1）或（-2，1）或（0，-1）. 易错警示 因为点P是运动的，所以要注意所有可能的情况，防止漏解.