《2025年5年中考3年模拟九年级数学下册沪科版》

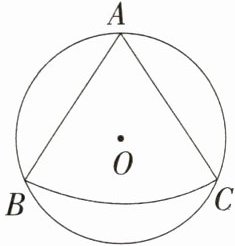
9.(2024黑龙江齐齐哈尔龙沙二模)如图，从一个直径为$4\sqrt{3}$ dm的圆形铁皮中剪出一个圆心角为60°的最大扇形ABC，并将剪下来的扇形围成一个圆锥，则圆锥的高为 ( )

A. $\sqrt{35}$ dm
B. $\sqrt{37}$ dm
C. $2\sqrt{35}$ dm
D. $2\sqrt{37}$ dm

答案：
A.设圆锥的底面半径为r。过圆心O作OD⊥AC于点D，连接AO，如图，易知$\angle DAO=\frac{1}{2}\angle BAC$。
∵$\angle BAC = 60^{\circ}$，
∴$\angle DAO = 30^{\circ}$，
∴$OD=\frac{1}{2}OA=\sqrt{3}$dm，
∴$AD=\sqrt{OA^{2}-OD^{2}} = 3$dm，
∴AC = 2AD = 6dm，
∴$\frac{60\pi\times6}{180}=2\pi r$，
∴圆锥的底面半径r = 1dm，
∴圆锥的高=$\sqrt{AC^{2}-r^{2}}=\sqrt{6^{2}-1^{2}}=\sqrt{35}$dm，故选A。

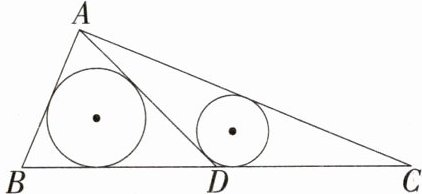
10.(2024湖北武汉模拟)如图，在Rt△ABC中，∠BAC = 90°，AD为中线，若AB = 5，AC = 12，设△ABD与△ACD的内切圆半径分别为$r_1$、$r_2$，则$\frac{r_1}{r_2}$的值为 ( )

A. $\frac{37}{23}$
B. $\frac{12}{5}$
C. $\frac{25}{18}$
D. $\frac{37}{33}$

答案：
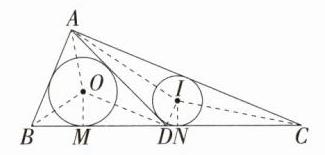
C.如图，连接OA，OB，OD，IA，IC，ID，过点O，点I分别作BC的垂线，垂足分别为M，N，在Rt△ABC中，$\angle BAC = 90^{\circ}$，AB = 5，AC = 12，
∴$BC=\sqrt{AC^{2}+AB^{2}} = 13$，
∵AD为中线，
∴$AD = BD = CD=\frac{1}{2}BC=\frac{13}{2}$，
∵$S_{\triangle ABD}=S_{\triangle ACD}$，
∴$\frac{1}{2}(AB + BD + AD)\cdot OM=\frac{1}{2}(AC + AD + CD)\cdot IN$，
∴$\frac{1}{2}\times(5 + 13)r_{1}=\frac{1}{2}\times(12 + 13)r_{2}$，
∴$\frac{r_{1}}{r_{2}}=\frac{25}{18}$。故选C。

11.(2023浙江绍兴中考)如图，四边形ABCD内接于圆O，若∠D = 100°，则∠B的度数是________.

答案： 80° 解析：
∵四边形ABCD内接于圆O，
∴$\angle B+\angle D = 180^{\circ}$，
∵$\angle D = 100^{\circ}$，
∴$\angle B = 80^{\circ}$。

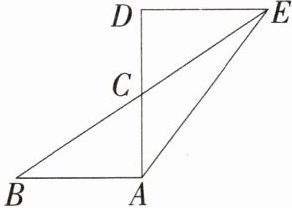
12.(2024北京北师大附中期末)如图，△DEC与△ABC关于点C成中心对称，AB = 3，AC = 2，∠CAB = 90°，则AE的长是________.

答案： 5 解析：
∵△DEC与△ABC关于点C成中心对称，
∴△ACB≌△DCE，
∴AC = CD = 2，$\angle BAD=\angle D = 90^{\circ}$，AB = DE = 3，
∴AD = 4，
∴$AE=\sqrt{DE^{2}+AD^{2}}=\sqrt{3^{2}+4^{2}} = 5$。

13. 陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一. 图②是从正面看到的一个“老碗”(图①)的形状示意图.$\overset{\frown}{AB}$是⊙O的一部分，D是$\overset{\frown}{AB}$的中点，连接OD，与弦AB交于点C，连接OA，OB. 若AB = 24 cm，碗深CD = 8 cm，则⊙O的半径OA为________.

答案： 13 cm 解析：
∵$\overset{\frown}{AB}$是⊙O的一部分，D是$\overset{\frown}{AB}$的中点，AB = 24 cm，
∴OD⊥AB，$AC = BC=\frac{1}{2}AB = 12$cm。设⊙O的半径OA为R cm，则OC = OD - CD=(R - 8)cm。在Rt△OAC中，$OA^{2}=AC^{2}+OC^{2}$，
∴$R^{2}=12^{2}+(R - 8)^{2}$，
∴R = 13，即⊙O的半径OA为13 cm。

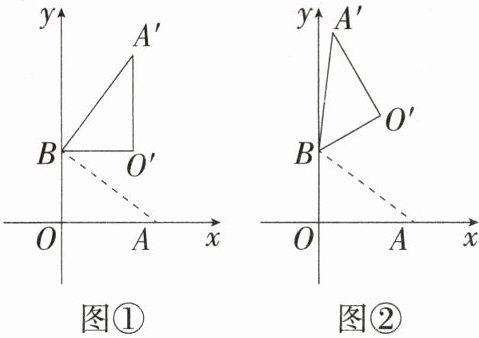
14.(2024湖南长沙麓山外国语实验中学月考)在平面直角坐标系中，O为原点，已知点A(4，0)，点B(0，3)，把△ABO绕点B逆时针旋转，得△A'BO'，点A，O旋转后的对应点为A'，O'，记旋转角为α.
(1)如图①，若α = 90°，则点A经过的路径长为________.
(2)如图②，若α = 120°，则点O'的坐标为________.

答案：

(1)$\frac{5\pi}{2}$
(2)$(\frac{3\sqrt{3}}{2},\frac{9}{2})$ 解析：
(1)
∵点A(4,0)，点B(0,3)，
∴OA = 4，OB = 3，
∵$\angle AOB = 90^{\circ}$，
∴$BA=\sqrt{OA^{2}+OB^{2}}=\sqrt{4^{2}+3^{2}} = 5$，如图①，
∵旋转角$\alpha = 90^{\circ}$，
∴点A的运动路径为以点B为圆心，半径为5且圆心角为90°的圆弧，
∴$l_{\overset{\frown}{AA'}}=\frac{90\times\pi\times5}{180}=\frac{5\pi}{2}$，
∴点A经过的路径长为$\frac{5\pi}{2}$。
(2)如图②，作O'C⊥y轴于点C，
∵旋转角$\alpha = 120^{\circ}$，
∴$\angle OBO' = 120^{\circ}$，
∴$\angle CBO' = 180^{\circ}-\angle OBO' = 60^{\circ}$，
∵$\angle BCO' = 90^{\circ}$，
∴$\angle BO'C = 30^{\circ}$，由旋转得O'B = OB = 3，
∴$BC=\frac{1}{2}O'B=\frac{3}{2}$，
∴$OC = 3+\frac{3}{2}=\frac{9}{2}$，$O'C=\sqrt{O'B^{2}-BC^{2}}=\sqrt{3^{2}-(\frac{3}{2})^{2}}=\frac{3\sqrt{3}}{2}$，
∴点O'的坐标为$(\frac{3\sqrt{3}}{2},\frac{9}{2})$。

15. [答案含评分细则](2024甘肃武威三模)(6分)如图，在⊙O中，AB、CD是直径，CE//AB且交⊙O于E，求证：$\overset{\frown}{BD}=\overset{\frown}{BE}$.

答案： 证明：连接OE(图略)，
∵CE//AB，
∴$\angle DOB=\angle C$，$\angle BOE=\angle E$， ……2分
∵OC = OE，
∴$\angle C=\angle E$， ……4分
∴$\angle DOB=\angle BOE$，
∴$\overset{\frown}{BD}=\overset{\frown}{BE}$。 ……6分