第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
11. (2015·安徽T15·8分)先化简,再求值:$(\frac{a^{2}}{a - 1} + \frac{1}{1 - a})\cdot\frac{1}{a}$,其中$a = -\frac{1}{2}$。
答案:
11.解:原式=$(\frac{a^{2}}{a-1}-\frac{1}{a-1})\cdot \frac{1}{a}=\frac{(a+1)(a-1)}{a-1}\cdot \frac{1}{a}=\frac{a+1}{a}$.当$a=-\frac{1}{2}$时,原式=-1.
12. (2023·安徽T15·8分)先化简,再求值:$\frac{x^{2} + 2x + 1}{x + 1}$,其中$x = \sqrt{2} - 1$。
答案:
12.解:原式=$\frac{(x+1)^{2}}{x+1}=x+1$.当$x=\sqrt{2}-1$时,原式=$\sqrt{2}-1+1=\sqrt{2}$.
命题点5 规律问题(7年7考)
13. (2023·安徽T18·8分)【观察思考】
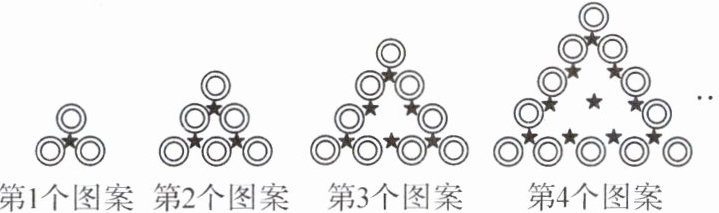
【规律发现】
请用含$n$的式子填空:
(1)第$n$个图案中“$◯$”的个数为
(2)第$1$个图案中“$\bigstar$”的个数可表示为$\frac{1×2}{2}$;第$2$个图案中“$\bigstar$”的个数可表示为$\frac{2×3}{2}$;第$3$个图案中“$\bigstar$”的个数可表示为$\frac{3×4}{2}$;第$4$个图案中“$\bigstar$”的个数可表示为$\frac{4×5}{2}$……第$n$个图案中“$\bigstar$”的个数可表示为
【规律应用】
(3)结合图案中“$\bigstar$”的排列方式及上述规律,求正整数$n$,使得连续的正整数之和$1 + 2 + 3 + \cdots + n$是第$n$个图案中“$◯$”的个数的$2$倍。
13. (2023·安徽T18·8分)【观察思考】

【规律发现】
请用含$n$的式子填空:
(1)第$n$个图案中“$◯$”的个数为
3n
;(2)第$1$个图案中“$\bigstar$”的个数可表示为$\frac{1×2}{2}$;第$2$个图案中“$\bigstar$”的个数可表示为$\frac{2×3}{2}$;第$3$个图案中“$\bigstar$”的个数可表示为$\frac{3×4}{2}$;第$4$个图案中“$\bigstar$”的个数可表示为$\frac{4×5}{2}$……第$n$个图案中“$\bigstar$”的个数可表示为
$\frac{n(n+1)}{2}$
;【规律应用】
(3)结合图案中“$\bigstar$”的排列方式及上述规律,求正整数$n$,使得连续的正整数之和$1 + 2 + 3 + \cdots + n$是第$n$个图案中“$◯$”的个数的$2$倍。
答案:
13.解:
(1)$3n$
(2)$\frac{n(n+1)}{2}$
(3)根据题意,得$\frac{n(n+1)}{2}=2× 3n$,解得$n=11$或$n=0$(不符合题意,舍去).$\therefore n$的值为11.
(1)$3n$
(2)$\frac{n(n+1)}{2}$
(3)根据题意,得$\frac{n(n+1)}{2}=2× 3n$,解得$n=11$或$n=0$(不符合题意,舍去).$\therefore n$的值为11.
14. (2024·安徽·T18·8分)数学兴趣小组开展探究活动,研究了“正整数$N$能否表示为$x^{2} - y^{2}$($x$,$y$均为自然数)”的问题。
(1)指导教师将学生的发现进行整理,部分信息如下($n$为正整数):
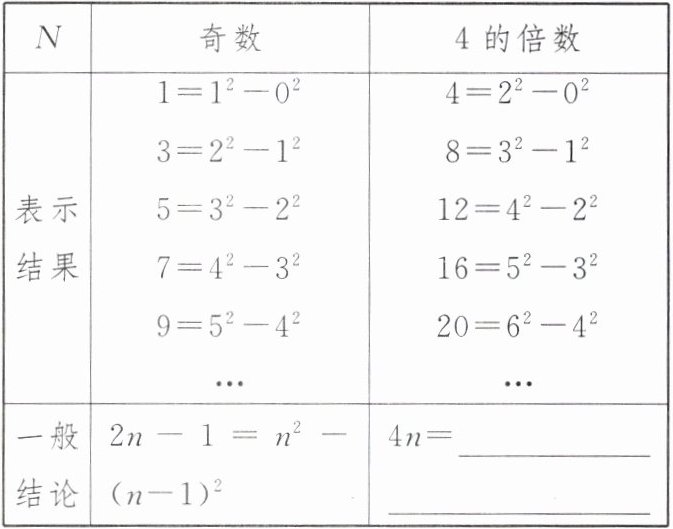
按上表规律,解答下列问题:
(ⅰ)$24 = ($____$)^{2} - ($____$)^{2}$;
(ⅱ)$4n =$
(2)兴趣小组还猜测:像$2$,$6$,$10$,$14$,$\cdots$这些形如$4n - 2$($n$为正整数)的正整数$N$不能表示为$x^{2} - y^{2}$($x$,$y$均为自然数)。
师生一起研讨,分析过程如下:
|假设$4n - 2 = x^{2} - y^{2}$,其中$x$,$y$均为自然数。分下列三种情形分析:|
|--|
|①若$x$,$y$均为偶数,设$x = 2k$,$y = 2m$,其中$k$,$m$均为自然数。则$x^{2} - y^{2} = (2k)^{2} - (2m)^{2} = 4(k^{2} - m^{2})$为$4$的倍数。而$4n - 2$不是$4$的倍数,矛盾。故$x$,$y$不可能均为偶数。|
|②若$x$,$y$均为奇数,设$x = 2k + 1$,$y = 2m + 1$,其中$k$,$m$均为自然数。则$x^{2} - y^{2} = (2k + 1)^{2} - (2m + 1)^{2} =$
|③若$x$,$y$一个是奇数一个是偶数,则$x^{2} - y^{2}$为奇数。而$4n - 2$是偶数,矛盾。故$x$,$y$不可能一个是奇数一个是偶数。|
|由①②③可知,猜测正确。|
阅读以上内容,请在情形②的横线上填写所缺内容。
(1)指导教师将学生的发现进行整理,部分信息如下($n$为正整数):

按上表规律,解答下列问题:
(ⅰ)$24 = ($____$)^{2} - ($____$)^{2}$;
(ⅱ)$4n =$
$(n+1)^{2}-(n-1)^{2}$
。(2)兴趣小组还猜测:像$2$,$6$,$10$,$14$,$\cdots$这些形如$4n - 2$($n$为正整数)的正整数$N$不能表示为$x^{2} - y^{2}$($x$,$y$均为自然数)。
师生一起研讨,分析过程如下:
|假设$4n - 2 = x^{2} - y^{2}$,其中$x$,$y$均为自然数。分下列三种情形分析:|
|--|
|①若$x$,$y$均为偶数,设$x = 2k$,$y = 2m$,其中$k$,$m$均为自然数。则$x^{2} - y^{2} = (2k)^{2} - (2m)^{2} = 4(k^{2} - m^{2})$为$4$的倍数。而$4n - 2$不是$4$的倍数,矛盾。故$x$,$y$不可能均为偶数。|
|②若$x$,$y$均为奇数,设$x = 2k + 1$,$y = 2m + 1$,其中$k$,$m$均为自然数。则$x^{2} - y^{2} = (2k + 1)^{2} - (2m + 1)^{2} =$
$4(k^{2}-m^{2}+k-m)$
为$4$的倍数。而$4n - 2$不是$4$的倍数,矛盾。故$x$,$y$不可能均为奇数。||③若$x$,$y$一个是奇数一个是偶数,则$x^{2} - y^{2}$为奇数。而$4n - 2$是偶数,矛盾。故$x$,$y$不可能一个是奇数一个是偶数。|
|由①②③可知,猜测正确。|
阅读以上内容,请在情形②的横线上填写所缺内容。
答案:
14.
(1)7 5 $(n+1)^{2}-(n-1)^{2}$
(2)$4(k^{2}-m^{2}+k-m)$
(1)7 5 $(n+1)^{2}-(n-1)^{2}$
(2)$4(k^{2}-m^{2}+k-m)$
查看更多完整答案,请扫码查看


