《2025年名校课堂中考总复习数学安徽专版》

10. 为缓解“停车难”的问题，某单位准备修建地下停车库，建筑设计师提供了该地下停车库的设计示意图，如图所示. 已知该坡道的水平距离 $ AB $ 为 $ 9 m $，坡面 $ AD $ 与 $ AB $ 的夹角 $ \angle BAD = 18^{\circ} $，石柱 $ BC = 0.5 m $，按规定，地下停车库坡道正上方 $ BC $ 处要张贴限高标志，以便告知停车人车辆能否安全驶入. 请你帮设计师计算一下 $ CE $ 的高度，以便张贴限高标志.（结果精确到 $ 0.1 m $，参考数据：$ \sin 72^{\circ} \approx 0.95 $，$ \cos 72^{\circ} \approx 0.31 $，$ \tan 72^{\circ} \approx 3.08 $，$ \sin 18^{\circ} \approx 0.31 $，$ \cos 18^{\circ} \approx 0.95 $，$ \tan 18^{\circ} \approx 0.32 $）

答案： 10.解：$\because\angle ABC=90^{\circ}$，$\angle BAD=18^{\circ}$，$\therefore\angle ADB=72^{\circ}$.在$Rt\triangle ABD$中，$AB=9\ m$，$\tan\angle BAD=\frac{BD}{AB}$，$\therefore BD=AB\cdot\tan\angle BAD\approx9×0.32=2.88(m)$.$\therefore CD=BD-BC=2.38\ m$.在$Rt\triangle CDE$中，$\sin\angle ADB=\frac{CE}{CD}$，$\therefore CE=CD\cdot\sin\angle ADB\approx2.38×0.95=2.261(m)$.结合实际情况，最终结果不得大于2.261m，$\therefore CE\approx2.2\ m$.答：CE的高度约为2.2m.

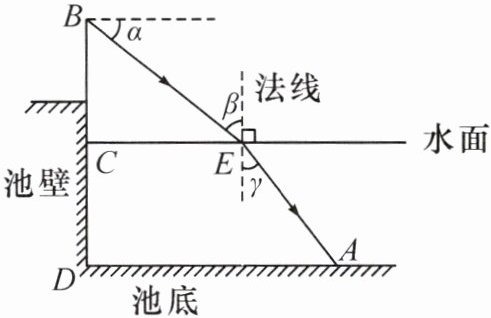
11. （2024·安徽）科技社团选择学校游泳池进行一次光的折射实验，如图，光线自点 $ B $ 处发出，经水面点 $ E $ 折射到池底点 $ A $ 处. 已知 $ BE $ 与水平线的夹角 $ \alpha = 36.9^{\circ} $，点 $ B $ 到水面的距离 $ BC = 1.20 m $，点 $ A $ 处水深为 $ 1.20 m $，到池壁的水平距离 $ AD = 2.50 m $. 点 $ B $，$ C $，$ D $ 在同一条竖直线上，所有点都在同一竖直平面内. 记入射角为 $ \beta $，折射角为 $ \gamma $，求 $ \frac{\sin \beta}{\sin \gamma} $ 的值（结果精确到 $ 0.1 $，参考数据：$ \sin 36.9^{\circ} \approx 0.60 $，$ \cos 36.9^{\circ} \approx 0.80 $，$ \tan 36.9^{\circ} \approx 0.75 $）

答案： 11.解：过点E作$EH\perp AD$于点H.由题意可知，$\angle CEB=\alpha=36.9^{\circ}$，$EH=1.20\ m$，$\therefore CE=\frac{BC}{\tan36.9^{\circ}}\approx\frac{1.20}{0.75}=1.60(m)$，$AH=AD-CE=2.50-1.60=0.90(m)$.$\therefore AE=\sqrt{AH^{2}+EH^{2}}=\sqrt{0.90^{2}+1.20^{2}}=1.50(m)$.$\therefore\sin\gamma=\frac{AH}{AE}=\frac{0.90}{1.50}=0.60$.$\because\sin\beta=\sin\angle CBE=\frac{CE}{BE}=\cos\angle CEB=\cos\alpha=0.80$，$\therefore\frac{\sin\beta}{\sin\gamma}=\frac{0.80}{0.60}\approx1.3$.