第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
4. 阅读下面材料,并解决相关问题:
如图,这是一个三角点阵,从上向下数有无数行,其中第一行有 1 个点,第二行有 2 个点,……,第 $ n $ 行有 $ n $ 个点……容易发现,三角点阵中前 4 行的点数之和为 10.
(1)探索:三角点阵中前 8 行的点数之和为
(2)体验:三角点阵中前 $ n $ 行的点数之和
(3)运用:某广场要摆放若干种造型的盆景,其中一种造型要用 420 盆同样规格的花,按照第一排 2 盆,第二排 4 盆,第三排 6 盆,……,第 $ n $ 排 $ 2n $ 盆的规律摆放而成,则一共能摆放多少排?

如图,这是一个三角点阵,从上向下数有无数行,其中第一行有 1 个点,第二行有 2 个点,……,第 $ n $ 行有 $ n $ 个点……容易发现,三角点阵中前 4 行的点数之和为 10.
(1)探索:三角点阵中前 8 行的点数之和为
36
,前 15 行的点数之和为120
,前 $ n $ 行的点数之和为$\frac{n(n+1)}{2}$
(用含 $ n $ 的代数式表示).(2)体验:三角点阵中前 $ n $ 行的点数之和
不能
(填“能”或“不能”)为 500.(3)运用:某广场要摆放若干种造型的盆景,其中一种造型要用 420 盆同样规格的花,按照第一排 2 盆,第二排 4 盆,第三排 6 盆,……,第 $ n $ 排 $ 2n $ 盆的规律摆放而成,则一共能摆放多少排?

答案:
4.解:
(1)36 120 $\frac{n(n+1)}{2}$
(2)不能
(3)由题可知,前$n$排盆景的总数可表示为$n(n+1)$.令$n(n+1)=420$,解得$n_{1}=-21$,$n_{2}=20$.
∵$n$为正整数,
∴$n=20$.
∴一共能摆放20排.
(1)36 120 $\frac{n(n+1)}{2}$
(2)不能
(3)由题可知,前$n$排盆景的总数可表示为$n(n+1)$.令$n(n+1)=420$,解得$n_{1}=-21$,$n_{2}=20$.
∵$n$为正整数,
∴$n=20$.
∴一共能摆放20排.
5. (2024·合肥二模)合肥近几年城市发展迅速,交通便利,2024 年计划再筑公路 533 km,深入推进“1155”大交通计划.修路的主要材料之一是沥青,沥青中含稠环芳香烃,其中偶数个苯环可视为同系物.注:最简单的稠环芳香烃是萘,它的分子结构图与结构简式如下:
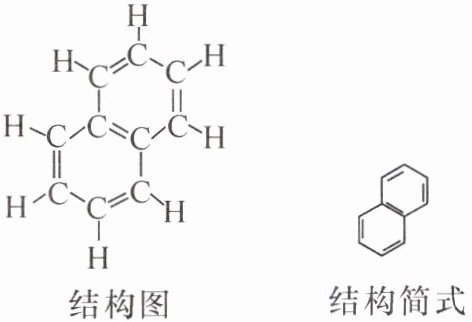
【观察思考】
观察结构简式的分子式,并回答下列问题:
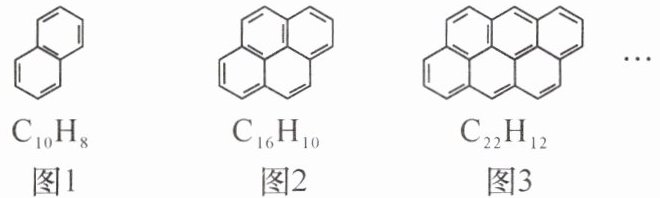
【规律发现】
(1)图 4 的分子中含
(2)图 $ n $ 的分子中含
【规律运用】
(3)若图 $ m $ 和图 $ m + 1 $ 的分子中共含有 242 个 C 原子,求 $ m $ 的值.

【观察思考】
观察结构简式的分子式,并回答下列问题:

【规律发现】
(1)图 4 的分子中含
28
个 C 原子;(2)图 $ n $ 的分子中含
(6n+4)
个 C 原子;【规律运用】
(3)若图 $ m $ 和图 $ m + 1 $ 的分子中共含有 242 个 C 原子,求 $ m $ 的值.
答案:
5.解:
(1)28
(2)$(6n+4)$
(3)由题意,得$6m+4+6(m+1)+4=242$,解得$m=19$.
∴$m$的值为19.
(1)28
(2)$(6n+4)$
(3)由题意,得$6m+4+6(m+1)+4=242$,解得$m=19$.
∴$m$的值为19.
查看更多完整答案,请扫码查看


