《2025年名校课堂中考总复习数学安徽专版》

3.（人教9上P57复习题T7变式）如图，用一段长为20m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m。当这个矩形菜园的长、宽各是多少时，菜园的面积最大？最大面积是多少？

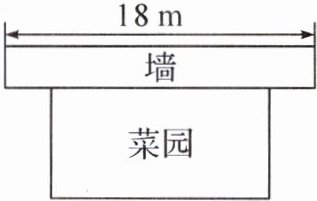
解：设矩形菜园的宽为$x$m，则长为m，根据墙长为18m，可得$x$的取值范围为，菜园的面积$S=$m²。把解析式化成$S=a(x - h)^2 +k$的形式：，∴当$x=$m时，矩形菜园的面积$S$最大，最大值为m²。

答案： 3.(20-2x) 1＜x＜10 x(20-2x) S=-2(x-5)²+50 5 50

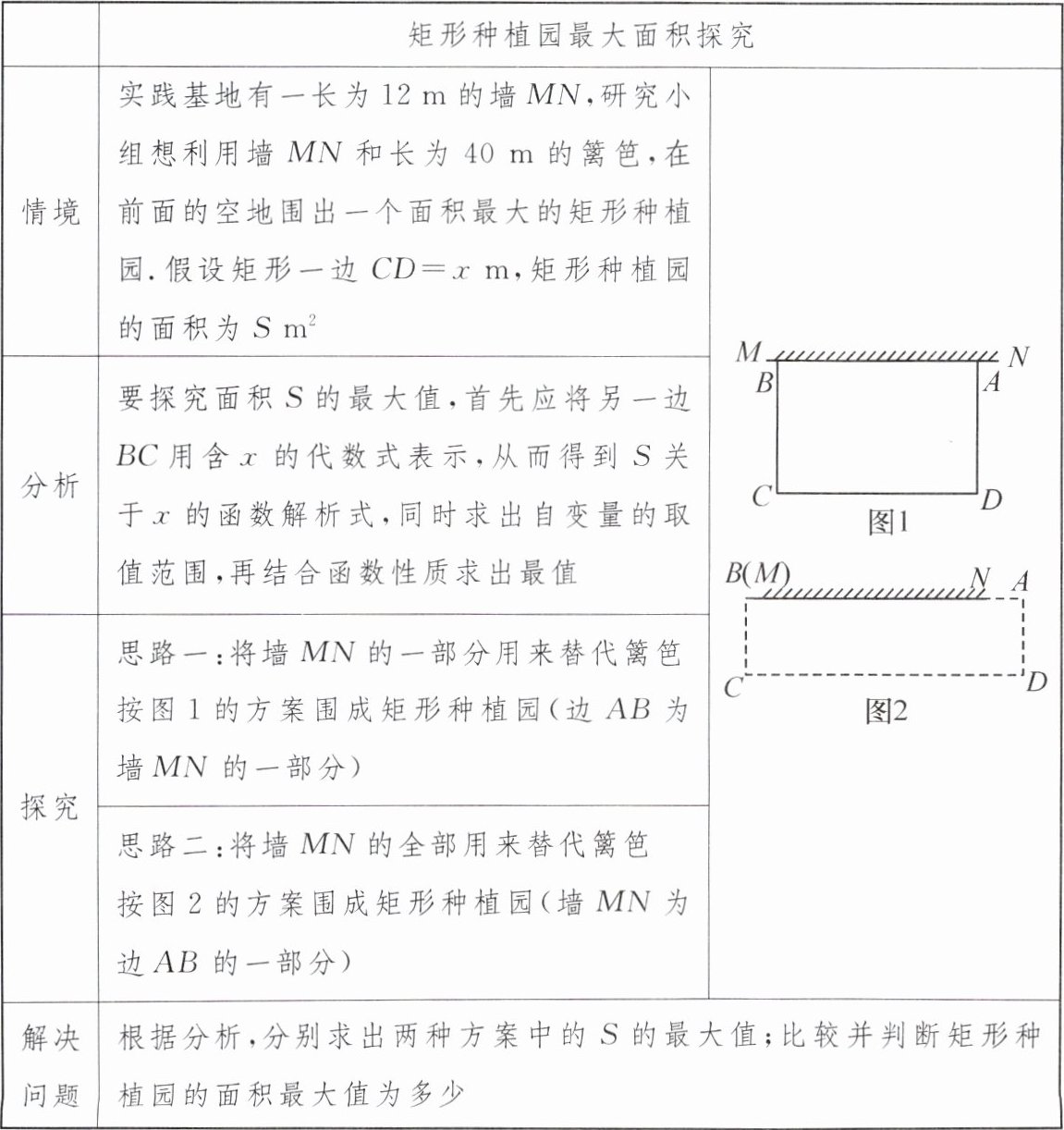
例 【2022·安徽T23核心考法】综合与实践：

答案： 典例精讲·稳拿基础 111 分
例 解:思路 1:设 CD=x m,则 BC=$\frac{40-x}{2}$ m,
∴S=x·$\frac{40-x}{2}$=-$\frac{1}{2}$x²+20x=-$\frac{1}{2}$(x-20)²+200,
∵-$\frac{1}{2}$＜0,0＜x≤12,
∴当 x=12 时,S$_{max}$=168.思路 2:设 AB=CD=x m,则 AD=BC=$\frac{40+12-2x}{2}$=(26-x)m,
∴S=x(26-x)=-x²+26x=-(x-13)²+169,
∵-1＜0,12≤x≤26,
∴当 x=13 时,S$_{max}$=169.
∵169＞168,
∴矩形种植园的面积最大为 169 m².