《2025年期末直通车八年级数学上册人教版》

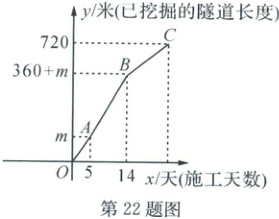
22. (10 分)近日，如通苏湖城际铁路湖州段顺利掘进开工。现有一条长为 $720$ 米的隧道，需甲、乙两个工程队合作完成。首先由甲工程队单独挖掘隧道 $m$ 米($m\leq 150$)，再由甲、乙两队共同施工，剩余任务由乙工程队单独完成。已挖掘的隧道长度 $y$ 米与施工天数 $x$ 天的关系如图所示。
(1) 甲、乙合作时，共施工9天，每天挖掘隧道40米。(2 分)
(2) 当 $m = 100$ 时，求第 $20$ 天时整个工程已完成多少米。(4 分)
(3) 已知乙工程队的施工效率不超过甲工程队，求完成这次任务的工期(天)范围。(4 分)

答案： 22.
(1)9 40
(2)解：当m=100时，A(5,100)，B(14,460)，V甲=20米/天，V乙=40-V甲=20米/天。设yBC=20x+b，将B(14,460)代入，所以460=20×14+b，所以b=180，所以yBC=20x+180。当x=20时，y=400+180=580，所以第20天时整个工程已完成580米。
(3)解：V甲=$\frac{m}{5}$米/天，V乙=40-V甲=(40-$\frac{m}{5}$)米/天，V甲≥V乙，即$\frac{m}{5}$≥40-$\frac{m}{5}$，所以m≥100，由题意可知m≤150，所以100≤m≤150。由
(2)可知，当m=100时，yBC=20x+180，20x+180=720，x=27；当m=150时，yBC=10x+370，10x+370=720，x=35。
答：完成这次任务的工期范围是27天至35天。

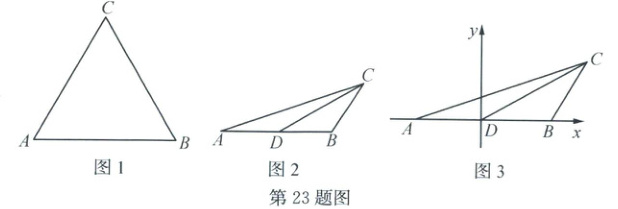
23. (10 分)定义：在一个三角形中，一边上的中线等于该边的$\frac{\sqrt{3}}{2}$倍，则称该三角形为“中根三角形”，该中线为三角形的“中根线”。
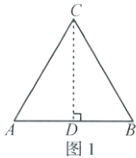
(1) 如图 1，$\triangle ABC$ 为等边三角形，且 $AB = 2$，证明：$\triangle ABC$ 为“中根三角形”。(4 分)
(2) 已知 $CD$ 为$\triangle ABC$的“中根线”，$AB = 2$。
① 如图 2，若 $BD = BC$，求$\triangle ABC$的面积。(4 分)
② 如图 3，以点 $D$ 为原点，$AB$ 所在直线为 $x$ 轴，建立平面直角坐标系。问：当 $b$ 为何值，有且只有一个点 $C$ 落在直线 $y = -\sqrt{3}x + b$ 上？若存在，请直接写出 $b$ 的值；若不存在，请说明理由。(2 分)

答案：
23.
(1)证明：如图，过点C作CD⊥AB。在等边三角形ABC中，因为AC=BC=AB=2，又CD⊥AB，所以AD=BD=1。在Rt△ACD中，由勾股定理，得CD=$\sqrt{3}$，所以CD=$\frac{\sqrt{3}}{2}$AB，所以△ABC是“中根三角形”。

(2)解：①如图2，过点B作BE⊥CD。由题意可知BD=AD=1。又因为CD为△ABC的“中根线”，所以CD=$\sqrt{3}$。在Rt△BDE中，由勾股定理，得BE=$\frac{1}{2}$，S△BCD=$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$。因为D是AB的中点，所以S△ABC=2S△BCD=$\frac{\sqrt{3}}{2}$。②b=±2$\sqrt{3}$。