《2025年期末直通车八年级数学上册人教版》

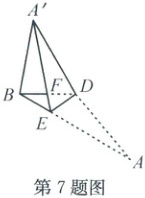
7. (2024·绍兴上虞)如图，在$\triangle ABD$中，$\angle ABD = 30^{\circ}$，$AB = 8$，$BD = 2\sqrt{3}$，$E$是$AB$边上一动点，沿$DE$把$\triangle ADE$翻折到$\triangle A'DE$的位置，使$A'E$与边$BD$交于点$F$，连结$A'B$。当$\triangle A'BF$是直角三角形时，$AE$的长为5.6或6。

答案：
7.5.6或6　解析:△A'BF为直角三角形有两种情况:
①∠A'BF=90°,如图1所示,过点D作DH⊥AB于点H,延长A'B,过点E作EG⊥A'B于点G。因为∠ABD=30°,BD=2$\sqrt{3}$,所以DH=$\sqrt{3}$,BH=3。因为AB=8,所以AH=AB−BH=5,所以AD=$\sqrt{AH^{2}+DH^{2}}$=$\sqrt{5^{2}+(\sqrt{3})^{2}}$=2$\sqrt{7}$。由折叠得A'E=AE,A'D=AD=2$\sqrt{7}$。因为∠A'BF=90°,EG⊥A'B,所以EG//BD,所以∠BEG=∠ABD=30°。令BE=x,则BG=$\frac{1}{2}$x,EG=$\frac{\sqrt{3}}{2}$x,AE=AB−BE=8−x,A'E =8−x。因为A'B=$\sqrt{A'D^{2}-BD^{2}}$=$\sqrt{(2\sqrt{7})^{2}-(2\sqrt{3})^{2}}$=4,所以A'G=A'B+BG=4+$\frac{1}{2}$x。因为A'G²+EG²=A'E²,所以(4+$\frac{1}{2}$x)²+($\frac{\sqrt{3}}{2}$x)²=(8−x)²,解得x=2.4,
∴AE=5.6;②∠A'FB=90°,如图2所示,此时由∠ABD=30°,得∠A'EB=60°,又因为∠A'ED=∠AED,所以∠A'ED=60°,所以易证△BFE≌△DFE(ASA),所以BF=FD=$\sqrt{3}$。令BE=y,则EF=$\frac{1}{2}$y,BF=$\frac{\sqrt{3}}{2}$y,所以$\frac{\sqrt{3}}{2}$y=$\sqrt{3}$,解得y=2,所以AE=6。综上所述，AE的长为5.6或6。

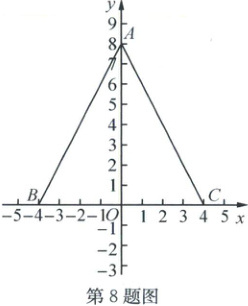
8. (2024·余姚)如图，在平面直角坐标系中，点$A(0,8)$，$B(-4,0)$，$C(4,0)$，给出如下定义:若$P$为$\triangle ABC$内(不含边界)一点，且$BP$与$\triangle APC$的一条边相等，则称点$P$为$\triangle ABC$的和谐点。
(1)在$P_1(-1,1)$，$P_2(2,2)$，$P_3(0,5)$中，$\triangle ABC$的和谐点是P₂,P₃。
(2)若点$P$为$\triangle ABC$的和谐点，且$\angle ABP = 45^{\circ}$，求点$P$的坐标。
(3)直线$l$为过点$M(0,m)$且与$x$轴平行的直线，若直线$l$上存在$\triangle ABC$的两个和谐点，请直接写出$m$的取值范围。

答案：
8.
(1)P₂,P₃　
(2)解:如图,作∠ABP=45°,B,P在直线l上。因为点P为△ABC的和谐点,所以BP=AP或BP=CP或BP=AC。
①若BP=AP,因为∠ABP=45°,所以∠BAP=45°。所以∠BPA=90°。过点P作PF⊥x轴于F,过点P作PE⊥y轴于E。因为∠BFP=∠APB=∠AEP=∠EOF=90°,所以∠EPF=90°。所以∠1+∠2=∠2+∠3=90°,所以∠1=∠3。在△BFP与△AEP中,因为$\begin{cases}\angle BFP=\angle AEP=90^{\circ},\\\angle1=\angle3,\\BP=AP.\end{cases}$所以△BFP≌△AEP(AAS)。所以PF=PE,BF=AE。设P(a,a),则有8−a=a−(−4),所以a=2,所以P(2,2);②若BP=CP,则点P在BC的中垂线上，即点P在y轴上。所以点P为直线l与y轴的交点。设直线l的表达式为y=kx+b,把(−4,0)，(2,2)代入，得$\begin{cases}-4k + b = 0,\\2k + b = 2,\end{cases}$解得$\begin{cases}k = \frac{1}{3},\\b = \frac{4}{3},\end{cases}$所以直线l的函数表达式为y=$\frac{1}{3}$x+$\frac{4}{3}$。当x=0时,y=$\frac{4}{3}$。所以P(0,$\frac{4}{3}$)。③若BP=AC,此时点P不存在。综上，P(2,2)或P(0,$\frac{4}{3}$)。
(3)$\frac{4}{3}$＜m＜4,且m≠3。